• «
• 1
• ...
• 63
• 64
• 65
• 66
• 67
• 68
• 69
• 70
• 71
• 72
• 73
• 74
• 75
• 76
• 77
• 78
• 79
• »

8.1 The advection equation

The classical advection equation is very often used as an example of a hyperbolic partial differential equation which illustrates many features of convection problems, while still being linear: $$ \begin{equation} \tag{8.1} \frac{\partial u}{\partial t} + a_0 \frac{\partial u}{\partial x} = 0 \end{equation} $$

Another convenient feature of the model equation (8.1) is that is has an analytical solution: $$ \begin{equation}\tag{8.2} u = u_0 \, f(x-a_0\,t ) \end{equation} $$ and represents a wave propagating with a constant velocity \( a_0 \) with unchanged shape. When \( a_0 > 0 \), the wave propagates in the positive x-direction, whereas for \( a_0 < 0 \), the wave propagates in the negative x-direction.

Equation (8.1) may serve as a model-equation for a compressible fluid, e.g if \( u \) denote pressure it represents a pressure wave propagating with the velocity \( a_0 \). The advection equation may also be used to model the propagation of pressure or flow in a compliant pipe, such as a blood vessel.

To allow for generalization we will also when appropriate write (8.1) on the following form: $$ \begin{equation} \frac{\partial u}{\partial t} + \frac{\partial F}{\partial x} = 0 \tag{8.3} \end{equation} $$ where for the linear advection equation \( F(u) = a_0\; u \).

8.2 Forward in time central in space discretization

We may discretize (8.1) with a forward difference in time and a central difference in space, normally abbreviated as the FTCS-scheme: $$ \begin{equation*} \tag{8.4} \frac{\partial u}{\partial t} \approx \frac{u_j^{n+1}-u_j^n}{\Delta t}, \qquad \frac{\partial u}{\partial x}\approx \frac{u_{j+1}^n-u_{j-1}^n}{2 \Delta x} \end{equation*} $$ and we may substitute the approximations (8.4) into the advection equation (8.1) to yield: $$ \begin{equation} \tag{8.5} u_j^{n+1} = u_j^n - \frac{C}{2}(u_{j+1}^n-u_{j-1}^n) \end{equation} $$ For convenience we have introduced the non-dimensional Courant-Friedrich-Lewy number (or CFL-number or Courant-number for short): $$ \begin{equation} \tag{8.6} C = a_0\frac{\Delta t}{\Delta x} \end{equation} $$

The scheme in (8.5) is first order in time and second order in space (i.e. \( (O(\Delta t) + O(\Delta x^2)) \)), and explicit in time as can bee seen both from Figure 103 and (8.5).

We will try to solve model equation (8.1) with the scheme (8.5) and initial conditions illustrated in Fig (104) with the mathematical representation: $$ \begin{equation*} \begin{array}{c} u(x,0) = 1 \text{ for } x < 0.5\\ u(x,0) = 0 \text{ for } x > 0.5 \end{array} \end{equation*} $$

Solutions for three CFL-numbers: C=0.25, 0.5 and 1.0 are illustrated in Figure 105. Large oscillations are observed for all values of the CFL-number, even though they seem to be slightly reduced for smaller C-values,; thus we have indications of an unstable scheme. As a first approach observe that the coefficient for \( u^n_{j+1} \) in (8.5) always will be negative, and thus the criterion of positive coefficients (PC-criterion) may not be satisfied for any value of \( C \).

However, as we know that the PC-criterion may be too strict in some cases, we proceed with a von Neumann analysis by introducing the numerical amplification factor \( G^n \) for the error \( E^n_j \) in the numerical scheme to be analyzed $$ \begin{equation} \tag{8.7} u^n_j\to E^n_j=G^n\cdot e^{i\cdot \beta x_j} \end{equation} $$ Substitution of (8.7) into (8.5) yields: $$ \begin{equation*} G^{n+1}e^{i\cdot \beta \cdot x_j} = G^ne^{i \cdot \beta \cdot x_j}-\frac{C}{2}\left(G^ne^{i\cdot \beta x_{j+1}}- G^ne^{i\cdot \beta x_{j-1}}\right) \end{equation*} $$ which after division with \( G^ne^{i\cdot \beta \cdot x_j} \) and introduction of the simplified notation \( \delta = \beta \cdot h \) yields: $$ \begin{equation*} G = 1 - \frac{C}{2}\left(e^{i\cdot \beta h}-e^{-i \cdot \beta h}\right) = 1 - i \cdot C \sin(\delta) \end{equation*} $$ where the trigonometric relations: $$ \begin{align} \tag{8.8} &2\cos(x)=e^{ix}+e^{-ix}\\ &i\cdot 2\sin(x)=e^{ix}-e^{-ix} \tag{8.9}\\ &\cos(x)=1-2\sin^2(\frac{x}{2}) \tag{8.10} \end{align} $$

have been introduced for convenience. Finally, we get the following expression for the numerical amplification factor: $$ \begin{equation*} |G|=\sqrt{1+C^2\sin^2(\delta)} \geq 1 \text{ for all } C \text{ and } \delta \end{equation*} $$ and consequently the FTCS-scheme is unconditionally unstable for the advection equation and is thus not a viable scheme. Even a very small value of C will not suffice to damp the oscillations.

8.3 Upwind schemes

Upwind differences are also called upstream differences. Numerically, this term indicates that we use backward differences with respect to the direction from which information is coming. Upwind differences are used only for convection terms, never for diffusive terms. Figure 106 shows a graphical interpretation of upwind differences when applied to the advection equation . The resulting scheme is called the upwind scheme.

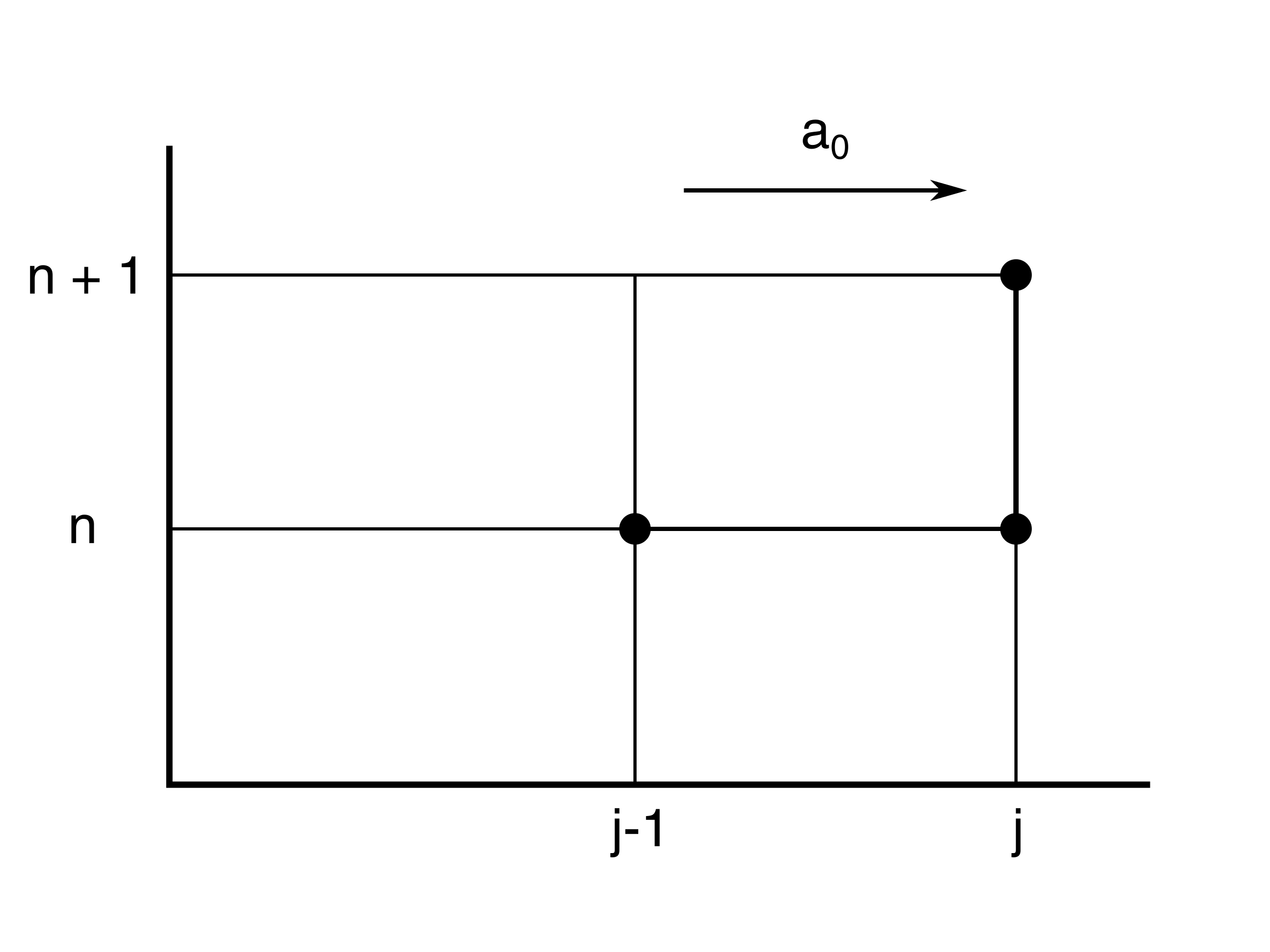
Upwind finite difference for the convective term: $$ \begin{equation} \frac{\partial u}{\partial x} = \frac{u_j^n-u_{j-1}^n}{\Delta x}+O(\Delta x) \tag{8.11} \end{equation} $$

Replacing (8.11) in (8.1) and using a forward difference for \( \frac{\partial u}{\partial t} \) and \( C = \frac{a_0 \Delta t}{\Delta x} \) yields: $$ \begin{equation} u_j^{n+1} = u_j^n - C \cdot (u_j^n - u_{j-1}^n) = (1-C)u_j^n + C \cdot u_{j-1}^n \tag{8.12} \end{equation} $$

(8.12) has an a truncation error of order \( O(\Delta t) + O(\Delta x) \)

If we set \( C=1 \) into (8.12), we get that \( u_j^{n+1}=u_{j-1}^n \), which in turn is the exact solution of the partial differential equation \( \frac{\partial u}{\partial t} + a_0 \frac{\partial u}{\partial x} = 0 \) ( see the section 5.2 First order partial differential equations). For \( C < 1 \) the wavefront of the numerical solution is smoothed, indicating that the scheme introduces a so called numerical viscosity for these values of \( C \). We will come back to the term numerical viscosity later on. Computational results shown in Figure 107 indicate that the scheme should be stable for \( C \leq 1 \). In fact, the PC criterion shows that the scheme should be stable for that range of \( C \). Let us use the von Neumann stability analysis to see if the stability range extends beyond that range. Insert (8.12) from (7.42) in the chapter 7 Diffusion problems: $$ \begin{equation*} G^{n+1}e^{i \cdot \beta \cdot x_j} = (1-C)\cdot G^ne^{i\cdot\beta\cdot x_j}+C\cdot G^ne^{i\cdot\beta\cdot x_{j-1}} \end{equation*} $$

dividing by \( G^ne^{i\cdot\beta\cdot x_j} \) gives: $$ \begin{equation*} G = (1-C) + C\cdot e^{-i\cdot\beta\cdot h} = 1-C + C\cdot (cos(\delta)-i\cdot \sin(\delta)) = 1+C\cdot (\cos(\delta)-1) -i\cdot C \cdot \sin(\delta) \end{equation*} $$ $$ \begin{equation} |G|= \sqrt{[1+C\cos(\delta-1)]^2 + C^2\sin^2(\delta)} = \sqrt{1-2C(1-\cos(\delta))\cdot(1-C)} \tag{8.13} \end{equation} $$

Enforcing the stability criterion \( |G|\leq1 \) results in the following: $$ \begin{equation*} 1-2C\cdot (1-\cos(\delta))\cdot(1-C) \leq 1 \Rightarrow C\cdot (1-\cos(\delta))\cdot(1-C) \geq 0 \end{equation*} $$

or $$ \begin{equation*} C\cdot \sin^2\left(\dfrac{\delta}{2}\right)(1-C) \geq 0 \end{equation*} $$

Stability interval: $$ \begin{equation} 0 < C\leq1 \tag{8.14} \end{equation} $$

(8.14) also applies when we set \( C=|a_0| \cdot \Delta t / \Delta x \). All stable explicit 2-level schemes for the advection equation have a restriction on the admissible Courant-number .

8.4 The modified differential equation

In the section 7.6 Truncation error, consistency and convergence we have seen how to determine the local truncation error and the consistency of numerical schemes. We will now see how to use a similar method to gain understanding on the stability of the resulting scheme. We will restrict the discussion to the linear advection equation

We recall the FTCS scheme from the section 8.2 Forward in time central in space discretization: $$ \begin{equation} \frac{u_j^{n+1}-u_j^n}{k}+a_0\frac{u_{j+1}^n-u_{j-1}^n}{2h}=0 \tag{8.15} \end{equation} $$

Inserting in (8.15) the Taylor expansions introduced in the section 7.6 Truncation error, consistency and convergence, such as (7.85), we obtain: $$ \begin{equation*} \begin{array}{l} \dfrac{1}{k}\left\{ \left[ u + ku_t + \frac{k^2}{2}u_{tt}+ \cdots \right]\Bigg|_j^n - u_j^n\right\} + \dfrac{a_0}{2h} \left[ u + hu_x + \frac{h^2}{2}u_{xx}+ \frac{h^3}{6}u_{xxx}+\cdots \right]\Bigg|_j^n\\\\ - \dfrac{a_0}{2h}\left[u - hu_x + \frac{h^2}{2}u_{xx}-\frac{h^3}{6}u_{xxx}+\cdots \right] \Bigg|_j^n = 0 \end{array} \end{equation*} $$

Reordering: $$ \begin{equation} \frac{\partial u}{\partial t} + a_0\frac{\partial u}{\partial x} = -\frac{k}{2}\frac{\partial^2u}{\partial t^2}-\frac{a_0 h^2}{6}\frac{\partial^3u}{\partial x^3}+\cdots \tag{8.16} \end{equation} $$

We now use the differential equation \( \frac{\partial u}{\partial t} + a_0\frac{\partial u}{\partial x}=0 \) to transform the term \( -\frac{k}{2}\frac{\partial^2u}{\partial t^2} \) in a spatial derivative.

The resulting differential equation is: $$ \begin{equation} \frac{\partial u}{\partial t} = -a_0\frac{\partial u}{\partial x} \tag{8.17} \end{equation} $$

Deriving with respect to \( t \): $$ \begin{equation*} \frac{\partial^2 u}{\partial t^2} = -a_0\frac{\partial^2 u}{\partial t \partial x} \end{equation*} $$

and then we derive (8.17) with respect to \( x \): $$ \begin{equation*} \frac{\partial^2 u}{\partial t \partial x} = -a_0\frac{\partial^2 u}{\partial x^2} \to -a_0\frac{\partial^2 u}{\partial t \partial x} = a_0^2\frac{\partial^2 u}{\partial x^2} \end{equation*} $$

so that we obtain: $$ \begin{equation} \frac{\partial^2 u}{\partial t^2} = a_0^2 \frac{\partial^2u}{\partial x^2} \tag{8.18} \end{equation} $$

Inserting (8.18) in (8.16): $$ \begin{equation*} \frac{\partial u}{\partial t}+ \ a_0 \frac{\partial u}{\partial x}= -\frac{ka_0^2}{2}\frac{\partial^2u}{\partial x^2} -\frac{a_0h^2}{6}\frac{\partial^3u}{\partial x^3}+ \cdots \end{equation*} $$

which, when introducing the Courant-number \( C=\frac{a_0 k}{h} \) gives: $$ \begin{equation} \frac{\partial u}{\partial t} +\ a_0 \frac{\partial u}{\partial x}= -\frac{Cha_0^2}{2}\frac{\partial^2u}{\partial x^2} -\frac{a_0h^2}{6}\frac{\partial^3u}{\partial x^3}+ \cdots \tag{8.19} \end{equation} $$

(8.19) clearly shows why the scheme in (8.15) is unstable. In computational fluid mechanics the term \( \nu_N = -\frac{C h a_0}{2} \) is often called numerical viscosity in analogy to the physical viscosity that accompanies the diffusive term of advection-diffusion equations like$\frac{\partial u}{\partial t} + a_0 {\partial u}{\partial x} = \nu \frac{\partial^2u}{\partial x^2}$ . When using the scheme given in (8.15), this results in solving the advection-diffusion equation with a negative viscosity coefficient , which is certainly unstable. (8.19) provides information on why oscillations in Figure 105 decrease for decreasing \( C \). Equation (8.19) is called the modified equation for a given numerical scheme, since it shows which is the differential problem that the scheme is actually solving and it therefore provides a deep insight in the behavior that the numerical solution will exhibit.

Now we will perform the same procedure as above but for the upwind scheme presented in the section 8.3 Upwind schemes. The scheme can be written as: $$ \begin{equation} \frac{u_j^{n+1}-u_j^n}{k}+a_0\frac{(u_j^n-u_{j-1}^n)}{h}=0 \tag{8.20} \end{equation} $$

After introducing Taylor expansions as before and reordering we get: $$ \begin{equation} \frac{\partial u}{\partial t} = a_0 \frac{\partial u}{\partial x}= -\frac{k}{2}\frac{\partial ^2 u}{\partial t^2}+\frac{a_0h}{2}\frac{\partial ^2 u}{\partial x^2}+\cdots \tag{8.21} \end{equation} $$

Since the differential equation is the same as for the FTCS scheme, we use the same procedure to replace time derivative terms with spatial derivative ones, yielding: $$ \begin{equation} \frac{\partial u}{\partial t} + a_0 \frac{\partial u}{\partial x} = \frac{a_0h}{2}(1-C)\frac{\partial^2 u}{\partial x^2}+\cdots \tag{8.22} \end{equation} $$

The coefficient \( \nu_N = \frac{a_0 h}{2}(1-C) \) is the so called numerical viscosity.

For \( C > 1 \) this term becomes negative and this in turn means that the scheme turns unstable. The necessary condition for stability is then \( C\leq1 \), in agreement with what seen before in terms of stability analysis. Note that the numerical viscosity increases with decreasing \( C \), meaning that sharp fronts will be smoothed more for lower Courant-numbers, as shown in Figure 107.

Remark: We have used the original differential equation for the derivation of both modified equations (8.19) and (8.22), i.e. \( \frac{\partial^2u}{\partial t^2} = a_0^2 \frac{\partial^2u}{\partial x^2} \). This procedure is called the Cauchy-Kowalewsky procedure. The problem is that the modified equation does not generally corresponds to the original equation, as expected. This means that instead of deriving the original equation, we have to derive (8.16) and (8.21). This procedure is called the Warming-Hyett procedure and must be generally adopted. For the above made computations, where we stop after one iteration of this procedure, both procedures are equivalent. For more complex differential equations the use of symbolic calculus programs such as Maple or Maxima becomes mandatory. The Maple-program below illustrate how to implement such procedure.

> restart:
> EQ:= (u(x,t+k)-u(x,t))/k + a*(u(x+h,t)-u(x-h,t))/(2*h):
> EQT:= mtaylor(EQ,[h,k]):
> MDE:=EQT:
> ELIM:=proc(i::integer,j::integer)
     local DE,uxt,UXT:
     global EQT,MDE:
     DE:=convert(diff(EQT,x$i,t$j-1,D): 
     uxt:=convert(diff(u(x,t),x$i,t$j),D):
     UXT:=solve(DE = 0,uxt):
     subs(uxt = UXT,MDE):
 end:
> MDE:=ELIM(0,2):
> MDE:=ELIM(1,1):
> MDE:=ELIM(0,3):
> MDE:=ELIM(1,2):
> MDE:=ELIM(2,1):
> # Substitute the Courant number C = a*k/h
> MDE:=expand(subs(k=C*h/a,MDE)):
> u2x:=convert(diff(u(x,t),x$2),D):
> u3x:=convert(diff(u(x,t),x$3),D):
> collect(MDE,[u2x,u3x]):
> RHSMDE:=-coeff(MDE,u2x)*convert(u2x,diff)
          -coeff(MDE,u3x)*convert(u3x,diff);

The resulting right-hand side of the modified equation delivered by the program is $$ \begin{equation*} \begin{array}{l} \text{RHSMDE:= } -\frac{1}{2}Cha\left( \frac{\partial^2}{\partial x^2}u(x,t) \right) - \left( \frac{1}{6}ah^2 + \frac{1}{3}C^2h^2a\right)\left( \frac{\partial^2}{\partial x^2}u(x,t) \right) \end{array} \end{equation*} $$

Note that in this case we have obtained the term \( \frac{1}{3}C^2h^2a \), which was missing in (8.19). The technique of the modified equation can be also applied to non-linear equations. Moreover, it can be shown that the method relates to von Neumann stability method. Hirsch [12] and Anderson [11] use the modified equation to study fundamental properties of finite difference schemes.

• «
• 1
• ...
• 63
• 64
• 65
• 66
• 67
• 68
• 69
• 70
• 71
• 72
• 73
• 74
• 75
• 76
• 77
• 78
• 79
• »