Numerical Methods for Engineers

3.2.1 Example: Large deflection of a cantilever

Figure 39: Large deflection of a beam subjected to a vertical load.

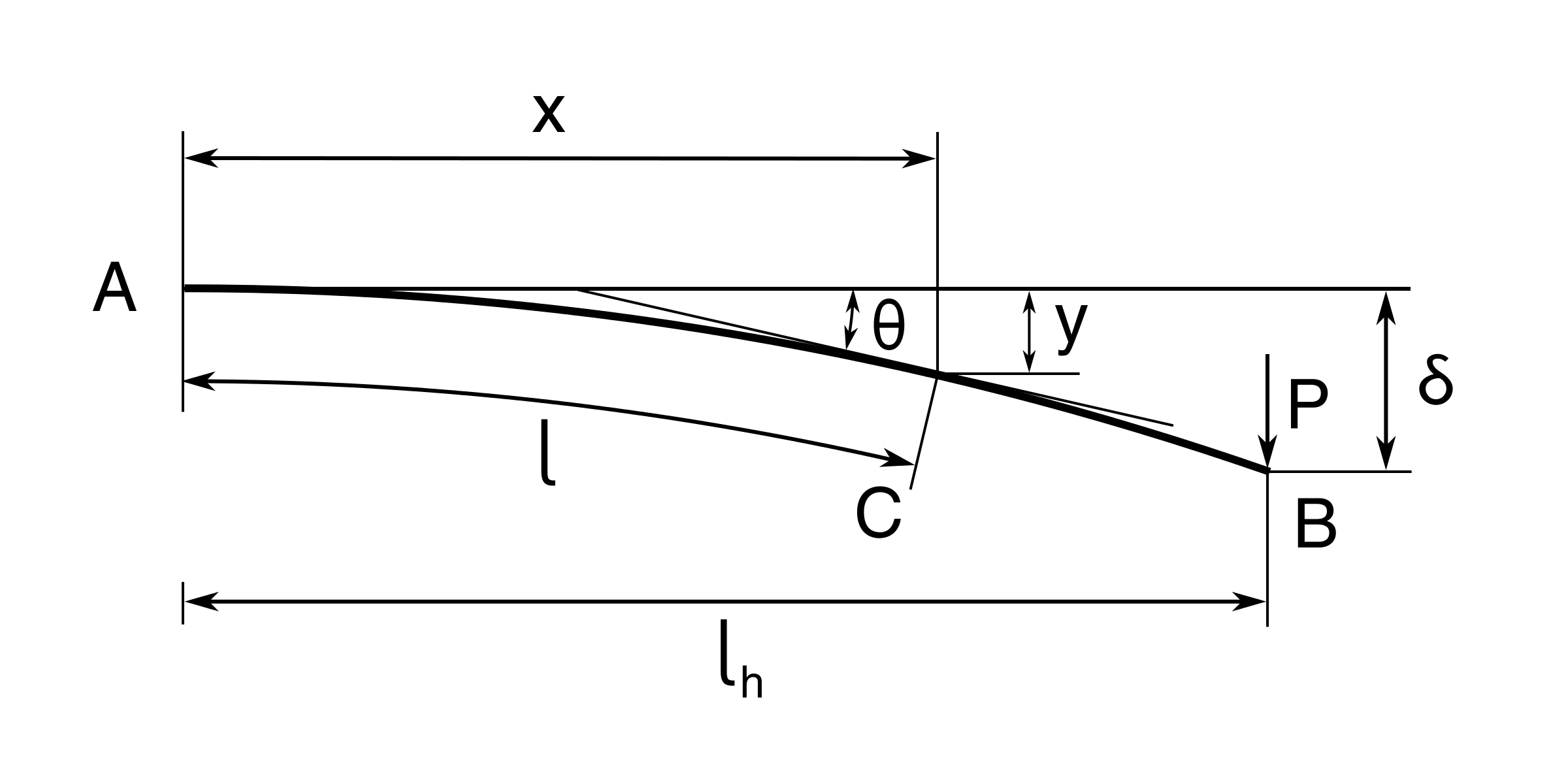
Consider a cantilever (see figure 39) which is anchored at one end $ A $ to a vertical support from which it is protruding. The cantilever is subjected to a structural load $ P $ at the other end $ B $. When subjected to a structural load, the cantilever carries the load to the support where it is forced against by a moment and shear stress [8]. In this example we will allow for large deflections and for that reason we introduce the arc length $ l $ and the angle of inclination $ \theta $ as variables.

All lengths are rendered dimensionless by division with the cantilever length $ L $. The arch length $ l $ ranges consequently from $ l=0 $ in $ A $ to $ l=1 $ in $ B $. Without further ado we present the differential equation for the elastic cantilever as: $$ \begin{equation} \kappa=\frac{d\theta}{L\cdot dl}=\frac{M}{EI} \tag{3.68} \end{equation} $$

where $ \kappa $ denotes the curvature, $ M $ the moment and $ EI $ flexural rigidity. The balance of moments in $ C $ may by computed as $ C $: $ M=P \cdot L(l_h-x) $ which by substitution in (3.68) results in: $$ \begin{equation} \frac{d\theta}{dl}=\frac{PL^2}{EI}(l_h-x) \tag{3.69} \end{equation} $$

From figure 39 we may deduce the following geometrical relations: $$ \begin{equation} \frac{dx}{dl}=\cos \theta,\ \frac{dy}{dl}=\sin \theta \tag{3.70} \end{equation} $$

Further, differentiation of (3.69) with respect to the arch length $ l $ and substitution of (3.70) yields: $$ \begin{equation} \frac{d^2\theta}{dl^2}+\frac{PL^2}{EI}\cos \theta =0 \tag{3.71} \end{equation} $$

For convenience we introduce the parameter $ \alpha $ which is defined as: $$ \begin{equation} \alpha^2=\frac{PL^2}{EI} \tag{3.72} \end{equation} $$

As a result we must solve the following differential equations: $$ \begin{equation} \frac{d^2\theta}{dl^2}+\alpha^2\cos \theta =0 \tag{3.73} \end{equation} $$ $$ \begin{equation} \frac{dy}{dl}=\sin \theta \tag{3.74} \end{equation} $$

with the following boundary conditions: $$ \begin{equation} y(0)=0,\ \theta (0)=0,\ \frac{d\theta}{dl}(1)=0 \tag{3.75} \end{equation} $$

The first two boundary conditions are due the anchoring in $ A $, whereas the latter is due to a vanishing moment in $ B $. The analytical solution of this problem may be found in appendix G, section G.3 in Numeriske Beregninger.

Numerical solution

First, we need to represent (3.73) and (3.74) as a system of first order differential equations. By introducing the conventions $ \theta=z_0,\ \theta'=z_1 $ and $ y=z_2 $ we get: $$ \begin{align} &z_0'=z_1 \nonumber \\ &z_1'=-\alpha^2\cos z_0 \tag{3.76} \\ &z_2'=\sin z_0 \nonumber \end{align} $$

with the boundary conditions $$ \begin{equation} z_0(0)=0,\ z_1(1)=0,\ z_2(0)=0 \tag{3.77} \end{equation} $$

We have to guess the initial value $ \theta'(0) $ such that the condition $ \frac{d\theta}{dl}(1)=0 $ is satisfied.

To do so, we let $ s=\theta'(0)=z_1(0) $ and $ \phi (s)=\theta'(1;s) - 0 = z_1(1) $. Consequently, we have to find $ s=s^* $ such that $ \phi (s^*)=0 $, which with z-variables takes the form: $ s=z_1(0) $.

With the introduction of these conventions the task at hand becomes to find $ s=s^* $ such that: $$ \begin{equation} \phi (s^*)=z_1(1;s^*)=0 \tag{3.78} \end{equation} $$

Additionally we find: $$ \begin{equation} l_h=\frac{s^*}{\alpha^2} \tag{3.79} \end{equation} $$

Due to the nonlinear nature of (3.76) the function (3.78) will be nonlinear too and we will use the secant method to find $ s^* $. To start the secant iterations we need two initial guesses $ s^0 $ and $ s^1 $. Suitable initial guesses may be found by first looking at $ \phi (s) $ graphically. The python-code phi_plot_beam_shoot.py produces Figure 40.

# src-ch2/phi_plot_beam_shoot.py;ODEschemes.py @ git@lrhgit/tkt4140/src/src-ch2/ODEschemes.py;

from ODEschemes import euler, heun, rk4
from numpy import cos, sin
import numpy as np
from matplotlib.pyplot import *

# change some default values to make plots more readable 
LNWDT=3; FNT=11
rcParams['lines.linewidth'] = LNWDT; rcParams['font.size'] = FNT



N=20
L = 1.0
y = np.linspace(0,L,N+1)

def f(z, t):
    """RHS for deflection of beam"""
    zout = np.zeros_like(z)
    zout[:] = [z[1],-alpha2*cos(z[0]),sin(z[0])]
    return zout 

solvers = [euler, heun, rk4] #list of solvers
solver=solvers[2] # select specific solver

alpha2 = 5.0 
beta=0.0 # Boundary value at y = L

N_guess = 30
s_guesses=np.linspace(1,5,N_guess)

z0=np.zeros(3)

phi = []
for s_guess in s_guesses:
    z0[1] = s_guess
    z = solver(f,z0,y)
    phi.append(z[-1,1] - beta)

legends=[] # empty list to append legends as plots are generated
plot(s_guesses,phi)

# Add the labels
legend(legends,loc='best',frameon=False) # Add the legends
title('alpha2 = ' + str(alpha2))
ylabel('phi')
xlabel('s')
grid(b=True, which='both')
show()

Figure 40: A plot of $ \phi(s) $ for $ \alpha^2 =5 $ for identification of zeros.

From visual inspection of Figure 40 we find that $ \phi $ as a zero at approximately $ s^*\approx3.05 $. Note, that the zeros depend on the values of $ \alpha $.

Given this approximation of the zero we may provide two initial guesses $ s^0=2.5 $ and $ s^1=5.0 $ which are 'close enough' for the secant method to converge. An example for how the solution may be found and presented is given in beam_deflect_shoot.py.

# src-ch2/beam_deflect_shoot.py;ODEschemes.py @ git@lrhgit/tkt4140/src/src-ch2/ODEschemes.py;

from ODEschemes import euler, heun, rk4
from numpy import cos, sin
import numpy as np
from matplotlib.pyplot import *

# change some default values to make plots more readable 
LNWDT=3; FNT=11
rcParams['lines.linewidth'] = LNWDT; rcParams['font.size'] = FNT



N=20
L = 1.0
y = np.linspace(0,L,N+1)

def dsfunction(phi0,phi1,s0,s1):
    if (abs(phi1-phi0)>0.0):   
        return    -phi1 *(s1 - s0)/float(phi1 - phi0)
    else:
        return 0.0


def f(z, t):
    """RHS for deflection of beam"""
    zout = np.zeros_like(z)
    zout[:] = [z[1],-alpha2*cos(z[0]),sin(z[0])]
    return zout 

alpha2 = 5.0 
beta=0.0 # Boundary value at y = L

solvers = [euler, heun, rk4] #list of solvers
solver=solvers[2] # select specific solver

# Guessed values
s=[2.5, 5.0]

z0=np.zeros(3)

z0[1] = s[0]
z = solver(f,z0,y)
phi0 = z[-1,1] - beta

nmax=10
eps = 1.0e-10
for n in range(nmax):
    z0[1] = s[1]
    z = solver(f,z0,y)
    phi1 = z[-1,1] - beta
    ds = dsfunction(phi0,phi1,s[0],s[1])
    s[0]  = s[1]
    s[1] +=  ds
    phi0 = phi1
    print('n = {}  s1 = {} and ds = {}'.format(n,s[1],ds))
    
    if (abs(ds)<=eps):
        print('Solution converged for eps = {} and s1 ={} and ds = {}. \n'.format(eps,s[1],ds))
        break

legends=[] # empty list to append legends as plots are generated

plot(y,z[:,0])
legends.append(r'$\theta$')

plot(y,z[:,1])
legends.append(r'$d\theta/dl$')

plot(y,z[:,2])
legends.append(r'$y$')



# Add the labels
legend(legends,loc='best',frameon=False) # Add the legends
ylabel(r'$\theta, d\theta/dl, y$')
xlabel('y/L')
#grid(b=True, which='both', axis='both',linestyle='-')
grid(b=True, which='both', color='0.65',linestyle='-')

show()

And the resulting output of solutions is illustrated in Figure 41

Figure 41: Solutions generated with a shooting method for large deflections of a cantilever subjected to a point load.