2.5 Differences
We will study some simple methods to solve initial value problems. Later we shall see that these methods also may be used to solve boundary value problems for ODEs.
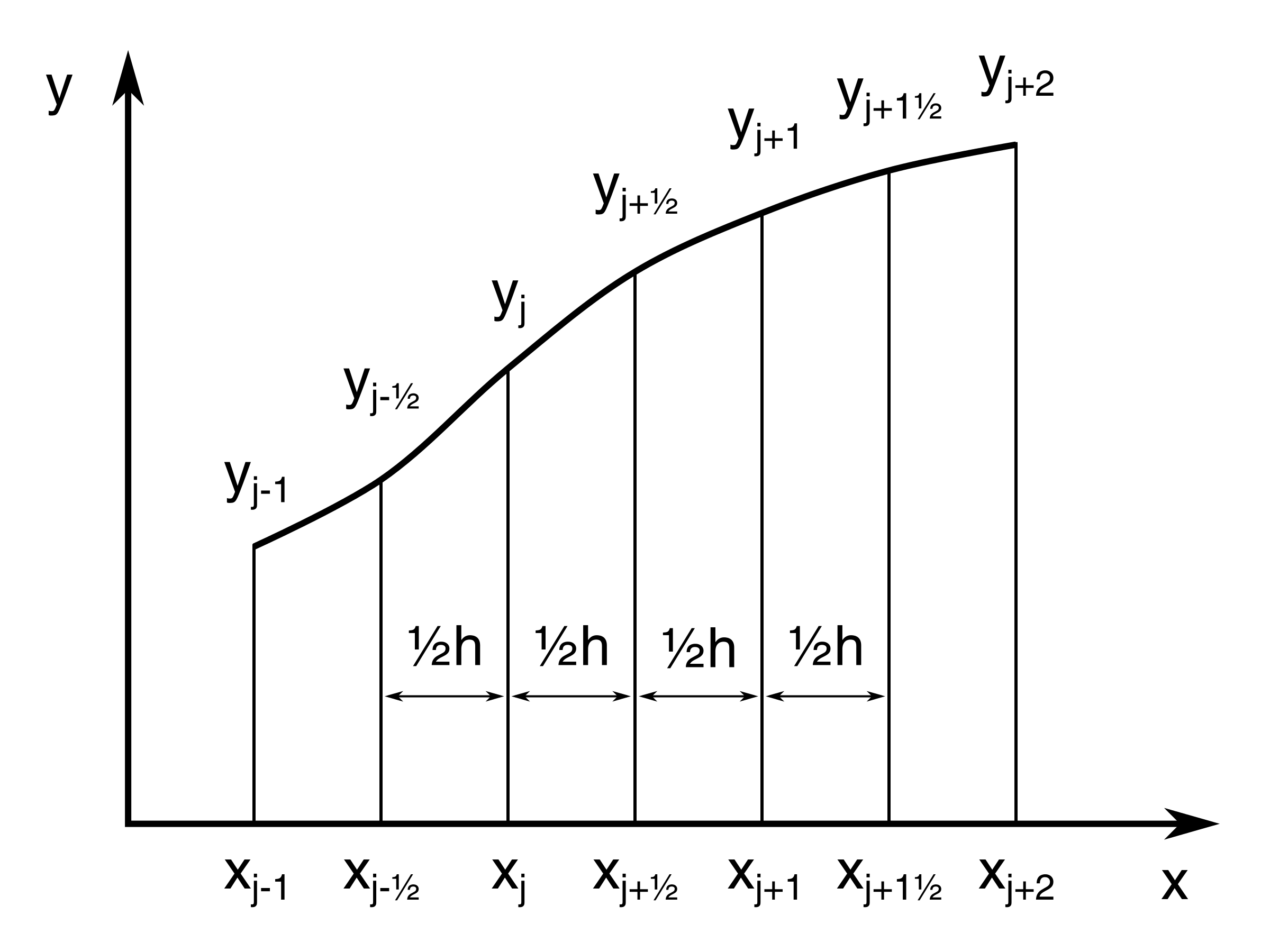
Figure 2: A generic function \( y(x) \) sampled at equidistant values of \( x \). .

For this purpose we need to introduce a suitable notation to enable us to formulate the methods in a convenient manner. In Figure 2) an arbitrary function \( y \) is illustrated as a continuous function of \( x \), i.e. \( y=y(x) \). Later \( y \) will be used to represent the solution of an ODE, which only may be represented and obtained for discrete values of \( x \). We represent these discrete, equidistant values of \( x \) by: $$ \begin{equation*} x_j=x_0+jh \end{equation*} $$ where \( h=\Delta x \) is assumed constant unless otherwise stated and \( j \) is an integer counter referring to the discrete values \( x_j \) for which the corresponding discrete value $$ \begin{equation*} y_j=y(x_j) \end{equation*} $$ may be found (see Figure 3).
Figure 3: Illustration of how to obtain difference equations.
Having introduced this notation we may the develop useful expressions and notations for forward differences, backward differences, and central differences, which will be used frequently later:
Forward differences: $$ \begin{equation*} \Delta y_j=y_{j+1}-y_j \end{equation*} $$
Backward differences: $$ \begin{equation} \tag{2.24} \nabla y_j=y_j-y_{j-1} \end{equation} $$
Central differences: $$ \begin{equation*} \delta y_{j+\frac{1}{2}}=y_{j+1}-y_j \end{equation*} $$
The linear difference operators \( \Delta \), \( \nabla \) and \( \delta \) are useful when we are deriving more complicated expressions. An example of usage is as follows, $$ \begin{equation*} \delta ^2y_j=\delta (\delta y_j)=\delta (y_{1+\frac{1}{2}}-y_{1-\frac{1}{2}}) =y_{j+1}-y_j-(y_j-y_{j-1})=y_{j+1}-2y_j+y_{j-1} \end{equation*} $$
However, for clarity we will mainly write out the formulas entirely rather than using operators.
We shall find difference formulas and need again:
The remainder \( R_n \) is given by $$ \begin{align} R_n&=\frac{1}{(n+1)!}y^{(n+1)}(\xi)\cdot (x-x_0)^{n+1} \tag{2.26}\\ &\text{where } \xi \in (x_0,x) \nonumber \end{align} $$
Now, Taylor's theorem (2.25) may be used to approximate the value of \( y(x_{j+1}) \), i.e. the forward value of \( y(x_{j}) \), by assuming that \( y(x_{j}) \) and it's derivatives are known: $$ \begin{align} \tag{2.27} y(x_{j+1}) \equiv &y(x_j+h)=y(x_j)+hy'(x_j) +\frac{h^2}{2}y''(x_j)+\\ &\dots+\frac{h^ny^{(n)}(x_j)}{n!}+R_n \nonumber \end{align} $$ where the remainder \( R_n=O(h^{n+1}),\ h\to 0 \).
From (2.27) we also get $$ \begin{equation} \tag{2.28} y(x_{j-1}) \equiv y(x_j-h)=y(x_j)-hy'(x_j)+\frac{h^2}{2}y''(x_j)+\dots+\frac{h^k(-1)^ky^{(k)}(x_j)}{k!}+\dots \end{equation} $$
In the following we will assume that \( h \) is positive. By solving (2.27) with respect to \( y' \) we may obtain a discrete forward difference approximation of \( y' \) at \( x_j \): $$ \begin{equation} \tag{2.29} y'(x_j)=\frac{y(x_{j+1})-y(x_j)}{h}+O(h) \end{equation} $$
By solving (2.28) with respect to \( y' \) we obtain a discrete approximation at \( x_i \): $$ \begin{equation} \tag{2.30} y'(x_j)=\frac{y(x_{j})-y(x_{j-1})}{h}+O(h) \end{equation} $$
By adding (2.28) and (2.27) together we get an approximation of the second derivative at the location \( x_j \): $$ \begin{equation} \tag{2.31} y''(x_j)=\frac{y(x_{j+1})-2y(x_{j})+y(x_{j-1})}{h^2}+O(h^2) \end{equation} $$
By subtraction of (2.28) from (2.27) we get a backward difference approximation of the first order derivative at the location \( x_j \): $$ \begin{equation} \tag{2.32} y'(x_j)=\frac{y(x_{j+1})-y(x_{j-1})}{2h}+O(h^2) \end{equation} $$
Notation:
We let \( y(x_j) \) always denote the function \( y(x) \) with \( x=x_j \). We use \( y_j \) both for the numerical and analytical value, the intended meaning is hopefully clear from the context.
Equations (2.29), (2.30), (2.31) and (2.32) then may be used to deduce the following difference expressions: $$ \begin{align} \tag{2.33} &y'_j=\frac{y_{j+1}-y_j}{h}\ ;\ \text{truncation error}\ O(h)\\ \tag{2.34} &y'_j=\frac{y_{j}-y_{j-1}}{h}\ ;\ \text{truncation error}\ O(h)\\ \tag{2.35} &y''_j=\frac{y_{j+1}-2y_j+y_{j-1}}{h^2}\ ;\ \text{truncation error}\ O(h^2)\\ \tag{2.36} &y'_j=\frac{y_{j+1}-y_{j-1}}{2h}\ ;\ \text{truncation error}\ O(h^2) \end{align} $$
In summary, equation (2.33) is a forward difference, (2.34) is a backward difference while (2.35) and (2.36) are central differences.
Figure 4: Illustration of how the discrete values may be used to estimate various orders of derivatives at location \( x_i \).
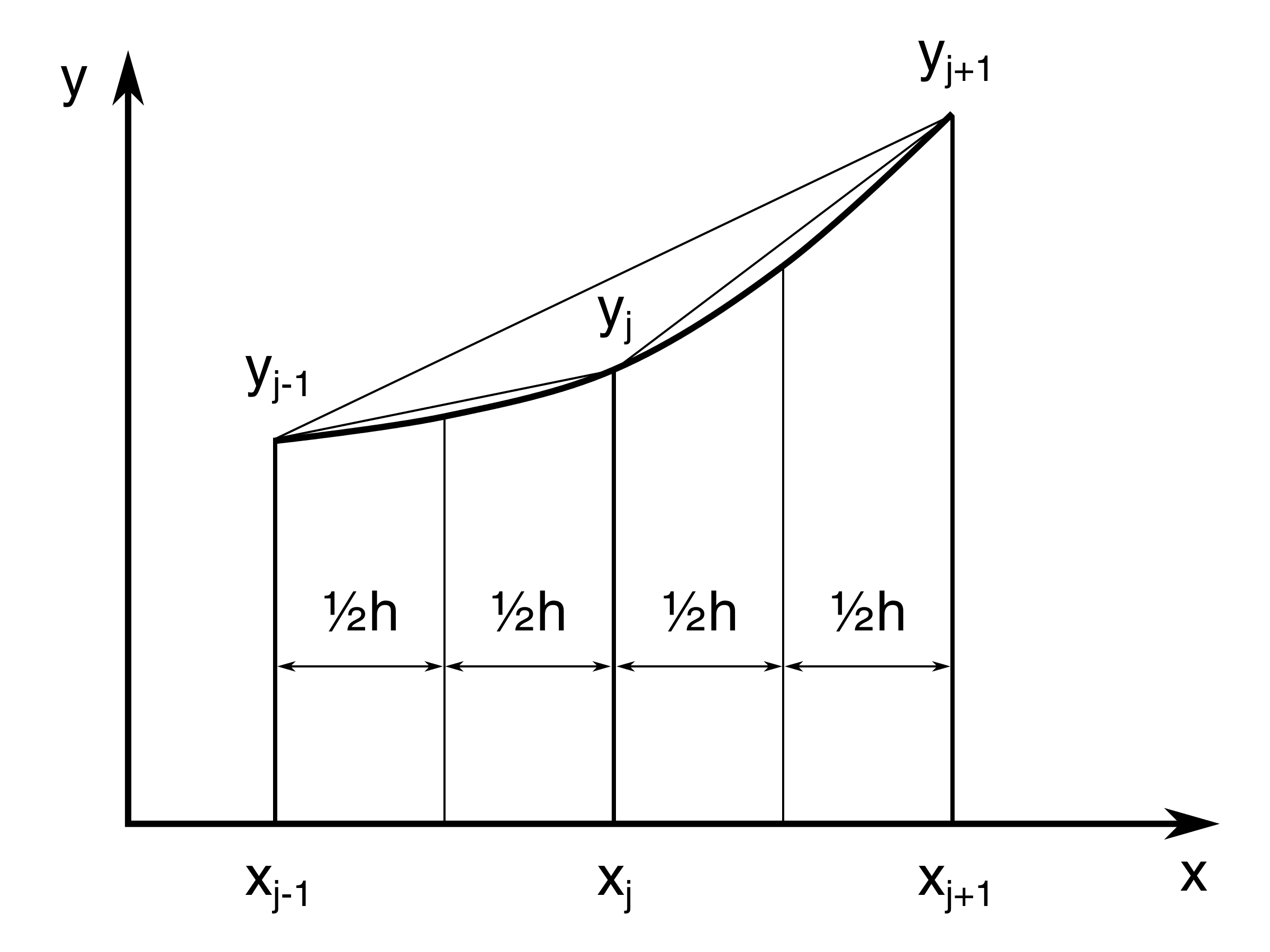
The expressions in (2.33), (2.34), (2.35) and (2.36) may also conveniently be established from Figure 4.
Whereas, (2.33) follows directly from the definition of the derivative, whereas the second order derivative (2.35) may be obtained as a derivative of the derivative by: $$ \begin{equation*} y''_j(x_j)=\left(\frac{y_{j+1}-y_j}{h}-\frac{y_{j}-y_{j-1}}{h}\right)\cdot \frac{1}{h} = \frac{y_{j+1}-2y_j+y_{j-1}}{h^2} \end{equation*} $$
and an improved expression for the derivative (2.36) may be obtained by averaging the forward and the backward derivatives: $$ \begin{equation*} y'_j=\left(\frac{y_{j+1}-y_j}{h} + \frac{y_{j}-y_{j-1}}{h}\right)\cdot \frac{1}{2}=\frac{y_{j+1}-y_{j-1}}{2h} \end{equation*} $$
To find the truncation error we proceed in a systematical manner by: $$ \begin{equation} \tag{2.37} y'(x_j)=a\cdot y(x_{j-1})+b\cdot y(x_j)+c\cdot y(x_{j+1})+O(h^m) \end{equation} $$
where we shall determine the constants \( a \), \( b \) and \( c \) together with the error term. For simplicity we use the notation \( y_j\equiv y(x_j),\ y'_j \equiv y'(x_j) \) and so on. From the Taylor series expansion in (2.27) and (2.28) we get $$ \begin{align} &a\cdot y_{j-1}+b\cdot y_j +c\cdot y_{j+1} = \nonumber \\ &a\cdot\left[y_j-hy'_j+\frac{h^2}{2}y''_j-\frac{h^3}{6}y'''_j(\xi)\right]+b\cdot y_j + \tag{2.38}\\ &c\cdot \left[y_j+hy'_j+\frac{h^2}{2}y''_j+\frac{h^3}{6}y'''_j(\xi)\right] \nonumber \end{align} $$
By collecting terms in equation (2.38) we get: $$ \begin{align} a\cdot y_{j-1}+b\cdot y_j +c\cdot y_{j+1} = \nonumber \\ (a+b+c) \, y_j+(c-a) \, h \, y'_j+ \tag{2.39} \\ (a+c) \, \frac{h^2}{2}y''_j + (c-a) \, \frac{h^3}{6} \, y'''(\xi) \nonumber \end{align} $$
From equation(2.39) we may then find \( a \), \( b \) and \( c \) such that \( y'_j \) gets as high accuracy as possible by : $$ \begin{align} a+b+c=0 \nonumber \\ (c-a)\cdot h=1 \tag{2.40}\\ \nonumber a+c=0 \end{align} $$ The solution to (2.40) is $$ \begin{equation*} a=-\frac{1}{2h},\ b=0 \text{ and } c=\frac{1}{2h} \end{equation*} $$ which when inserted in (2.37) gives $$ \begin{equation} \tag{2.41} y'_j=\frac{y_{j+1}-y_{j-1}}{2h}-\frac{h^2}{6}y'''(\xi) \end{equation} $$
By comparison of (2.41) with (2.37) we see that the error term is \( O(h^m)=-\frac{h^2}{6}y'''(\xi) \), which means that \( m=2 \). As expected, (2.41) is identical to (2.32).
Let's use this method to find a forward difference expression for \( y'(x_j) \) with accuracy of \( O(h^2) \). Second order accuracy requires at least three unknown coefficients. Thus, $$ \begin{equation} \tag{2.42} y'(x_j)=a\cdot y_j + b\cdot y_{j+1} + c\cdot y_{j+2} + O(h^m) \end{equation} $$ The procedure goes as in the previous example as follows, $$ \begin{align*} a&\cdot y_{j}+b\cdot y_{j+1} +c\cdot y_{j+2} =\\ a&\cdot y_j+b\cdot\left[y_j+hy'_j+\frac{h^2}{2}y''_j+\frac{h^3}{6}y'''(\xi)\right]+\\ c&\cdot \left[y_j+2hy'_j+2h^2y''_j+\frac{8h^3}{6}y'''_j(\xi)\right]\\ =&(a+b+c)\cdot y_j+(b+2c)\cdot hy'_j \\ +& h^2\left(\frac{b}{2}+2c\right)\cdot y''_j+\frac{h^3}{6}(b+8c)\cdot y'''(\xi) \end{align*} $$ We determine \( a \), \( b \) and \( c \) such that \( y'_j \) becomes as accurate as possible. Then we get, $$ \begin{align} a+b+c=0 \nonumber\\ (b+2c)\cdot h=1 \tag{2.43}\\ \frac{b}{2}+2c=0\nonumber \end{align} $$ The solution of (2.43) is $$ \begin{equation*} a=-\frac{3}{2h},\ b=\frac{2}{h},\ c=-\frac{1}{2h}\ \end{equation*} $$ which inserted in (2.42) gives $$ \begin{equation} \tag{2.44} y'_j=\frac{-3y_j+4y_{j+1}-y_{j+2}}{2h}+\frac{h^2}{3}y'''(\xi) \end{equation} $$ The error term \( O(h^m)=\frac{h^2}{3}y'''(\xi) \) shows that \( m=2 \).
Here follows some difference formulas derived with the procedure above:
2.5.1 Example: Discretization of a diffusion term
This diffusion term \( \frac{d}{dx} \left ( p(x) \frac{d}{dx} u(x)\right ) \) often appears in difference equations, and it may be beneficial to treat the term as it is instead of first execute the differentiation. Below we will illustrate how the diffusion term may be discretized with the three various difference approaches: forward, backward and central differences.
Central differences: We use central differences (recall Figure 3) as follows, $$ \begin{align*} \frac{d}{dx}\left (p(x)\cdot \frac{d}{dx}u(x)\right )\bigg|_i \approx& \frac{[p(x)\cdot u'(x)]|_{i+\frac{1}{2}}-[p(x)\cdot u'(x)]|_{i-\frac{1}{2}}}{h}\\ =& \frac{p(x_{i+\frac{1}{2}})\cdot u'(x_{i+\frac{1}{2}})-p(x_{i-\frac{1}{2}})\cdot u'(x_{i-\frac{1}{2}})}{h} \end{align*} $$ Using central differences again, we get $$ \begin{equation*} u'(x_{i+\frac{1}{2}}) \approx \frac{u_{i+1}-u_i}{h},\ u'(x_{i-\frac{1}{2}}) \approx \frac{u_{i}-u_{i-1}}{h},\ \end{equation*} $$ which inserted in the previous equation gives the final expression $$ \begin{equation} \tag{2.45} \frac{d}{dx}\left (p(x)\cdot \frac{d}{dx}u(x)\right )\bigg|_i \approx \frac{p_{i-\frac{1}{2}}\cdot {u_{i-1}-(p_{i+\frac{1}{2}}+p_{i-\frac{1}{2}})\cdot u_i+p_{i+\frac{1}{2}}\cdot u_{i+1}}}{h^2} + \text{error term} \end{equation} $$ where $$ \begin{equation*} \text{error term} =-\frac{h^2}{24}\cdot \frac{d}{dx} \bigg(p(x)\cdot u'''(x)+[p(x)\cdot u'(x)]''\bigg) + O(h^3) \end{equation*} $$ If \( p(x_{1+\frac{1}{2}}) \) and \( p(x_{1-\frac{1}{2}}) \) cannot be found directly, we use $$ \begin{equation} \tag{2.46} p(x_{1+\frac{1}{2}})\approx \frac{1}{2}(p_{i+1}+p_i),\ p(x_{1-\frac{1}{2}}) \approx \frac{1}{2}(p_i+p_{i-1}) \end{equation} $$ Note that for \( p(x)=1=\text{constant} \) we get the usual expression $$ \begin{equation*} \frac{d^2u}{dx^2}\bigg|_i=\frac{u_{i+1}-2u_i+u_{i-1}}{h^2}+O(h^2) \end{equation*} $$ Forward differences: We start with $$ \begin{align*} \frac{d}{dx}\left (p(x)\cdot \frac{du}{dx}\right )\bigg|_i &\approx \frac{p(x_{i+\frac{1}{2}})\cdot u'(x_{i+\frac{1}{2}})-p(x_i)\cdot u'(x_i)}{\frac{h}{2}}\\ &\approx \frac{p(x_{i+\frac{1}{2}})\cdot\left( \frac{u_{i+1}-u_i}{h}\right) -p(x_i)\cdot u'(x_i)}{\frac{h}{2}} \end{align*} $$ which gives $$ \begin{equation} \tag{2.47} \frac{d}{dx}\left (p(x)\cdot \frac{du}{dx}\right )\bigg|_i = \frac{2\cdot [p(x_{i+\frac{1}{2}})\cdot {(u_{i+1}-u_i)-h\cdot p(x_i)\cdot u'(x_i)]}}{h^2} +\text{error term} \end{equation} $$ where $$ \begin{equation} \tag{2.48} \text{error term} =- \frac{h}{12}[3p''(x_i)\cdot u'(x_i)+6p'(x_i)\cdot u''(x_i)+4p(x_i)\cdot u'''(x_i)]+O(h^2) \end{equation} $$ We have kept the term \( u'(x_i) \) since (2.47) usually is used at the boundary, and \( u'(x_i) \) may be prescribed there. For \( p(x)=1=\text{constant} \) we get the expression $$ \begin{equation} \tag{2.49} u''_i = \frac{2\cdot [u_{i+1}-u_i-h\cdot u'(x_i)]}{h^2}-\frac{h}{3}u'''(x_i)+O(h^2) \end{equation} $$
Backward Differences: We start with $$ \begin{align*} \frac{d}{dx}\left (p(x)\frac{du}{dx}\right )\bigg|_i \approx& \frac{p(x_i)\cdot u'(x_i)-p(x_i)\cdot u'(x_{i-\frac{1}{2}})\cdot u'(x_{i-\frac{1}{2}})}{\frac{h}{2}}\\ \approx& \frac{p(x_i)\cdot u'(x_i)-p(x_{i-\frac{1}{2}})\left(\frac{u_i-u_{i-1}}{h}\right)}{\frac{h}{2}} \end{align*} $$ which gives $$ \begin{equation} \tag{2.50} \frac{d}{dx}\left (p(x)\frac{du}{dx}\right )\bigg|_i = \frac{2\cdot [h\cdot p(x_i)u'(x_i)-p(x_{i-\frac{1}{2}})\cdot (u_i-u_{i-1})]}{h^2}+\text{error term} \end{equation} $$ where $$ \begin{equation} \tag{2.51} \text{error term}=\frac{h}{12}[3p''(x_i)\cdot u'(x_i)+6p'(x_i)\cdot u''(x_i)+4p(x_i)\cdot u'''(x_i)]+O(h^2) \end{equation} $$ This is the same error term as in (2.48) except from the sign. Also here we have kept the term \( u'(x_i) \) since (2.51) usually is used at the boundary where \( u'(x_i) \) may be prescribed. For \( p(x)=1=\text{constant} \) we get the expression $$ \begin{equation} u''_i = \frac{2\cdot [h\cdot u'(x_i)-(u_i-u_{i-1})]}{h^2}+\frac{h}{3}u'''(x_i)+O(h^2) \tag{2.52} \end{equation} $$