15
6 Elliptic partial differential equations
6.1 Introduction
Important and frequently occurring practical problems are governed by elliptic PDEs, including steady-state temperature distribution in solids.
- Laplace:
- Poisson:
- Helmholtz:
The 2D versions of the famous equations above are special cases of the a generic elliptic PDE may be represented by: $$ \begin{equation} \frac{\partial}{\partial x}\left(a\frac{\partial u}{\partial x}\right)+\frac{\partial}{\partial y}\left(b\frac{\partial u}{\partial y}\right) +c\cdot u = q \tag{6.4} \end{equation} $$
where \( a \), \( b \), \( c \) and \( q \) may be functions of \( x \) and \( y \) and \( a \) and \( b \) have the same sign.
- Transient heat conduction is governed by:
From the classification approach in the chapter 5.3 Second order partial differenatial equations (see also Classification of linear 2nd order PDEs) we see that (6.1) to (6.3) are elliptic, meaning no real characteristics. Therefore, elliptic PDEs must be treated as boundary value problems (see 5.4 Boundary conditions for 2nd order PDEs) for a discussion about the conditions for a well posed problem).
For the solution of a generic elliptic PDE like (6.4), in a domain in two-dimensions bounded by the boundary curve C (73), we reiterate the most common boundary value conditions from 5.4 Boundary conditions for 2nd order PDEs:
- Dirichlet-condition: \( u(x,y)=G_1(x,y) \) on the boundary cure C
- Neumann-condition: \( \dfrac{\partial u}{\partial n}=G_2(x,y) \) on C
- Robin-condition: \( a\cdot u(x,y)+b\cdot \dfrac{\partial u(x,y)}{\partial n}= G_3(x,y) \) on C
Figure 73: A solution domain in two-dimensions bounded by a boundary curve C.
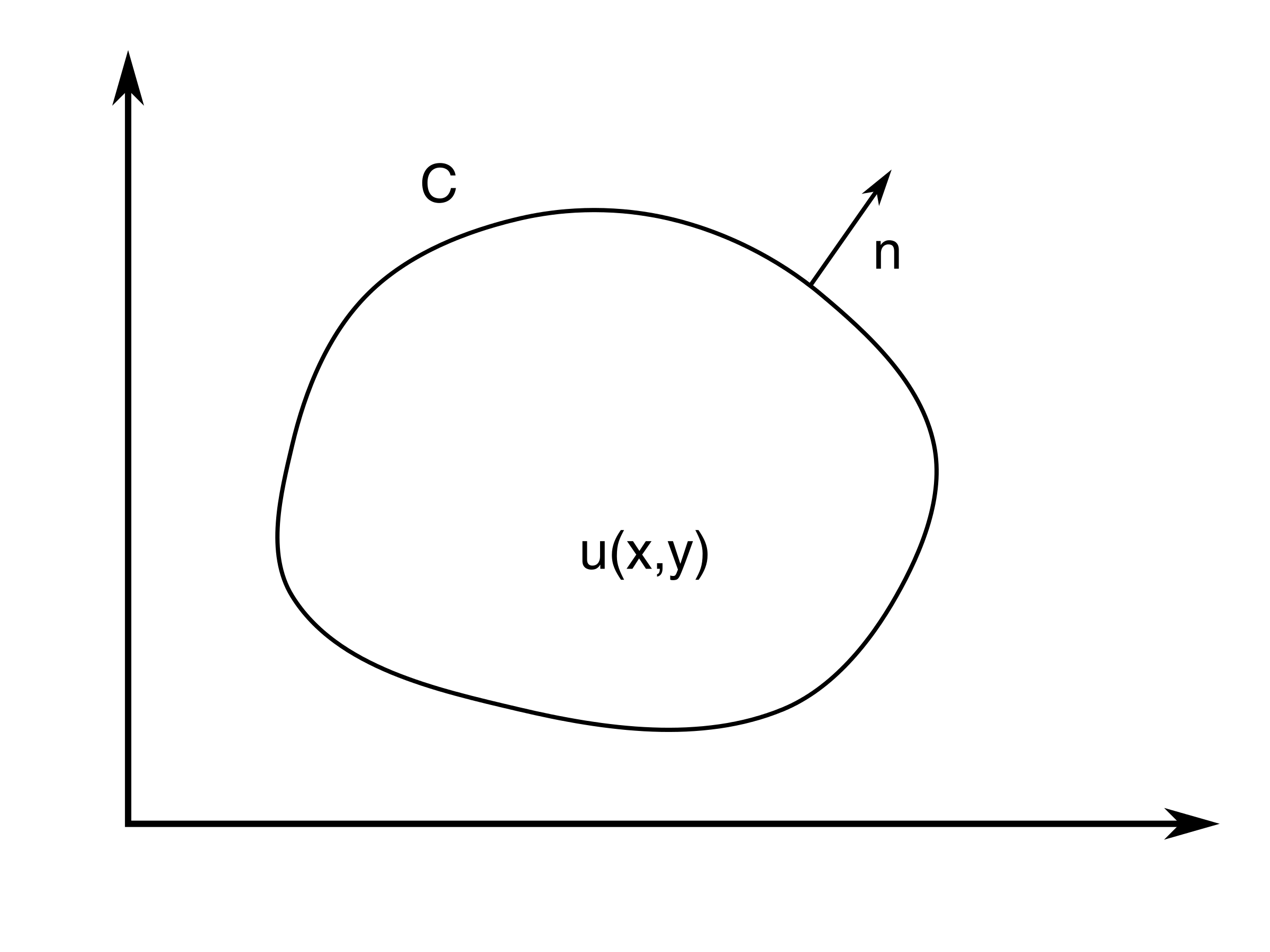
For the Neuman-problem, at least one value of \( u(x,y) \) must be specified on \( C \) for the solution to be unique. Additionally, the contour integral of \( G_2(x,y) \) on \( C \) must vanish.
Several physical problems may be modeled by the Poisson equation (6.2)
- The stress equation for torsion of an elastic rod
- The displacement of an membrane under constant pressure.
- Stokes flow (low Reynolds number flow)
- Numerous analytical solutions (also in polar coordinates) may be found in [10] section 3-3.