3.5 Exercises
Exercise 5: Stokes first problem for a non-Newtonian fluid
Figure 51: Stokes first problem for a non-Newtonian fluid: schematic representation of the velocity profile.
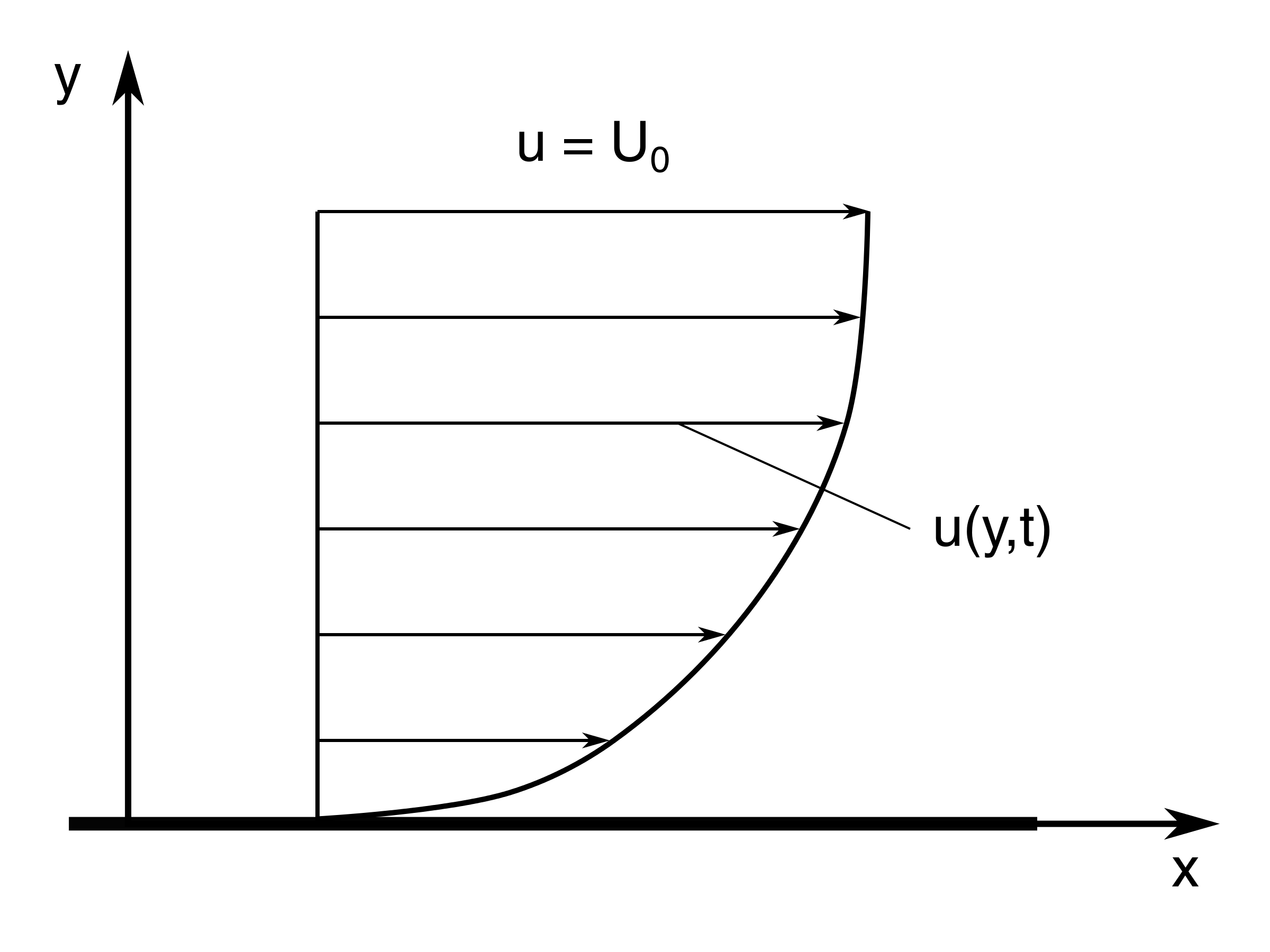
A non-Newtonian fluid flows in the plane with constant velocity \( U_0 \), paralell with the \( x \)-axis. At time \( t=0 \) we insert a thin plate into the flow, paralell to the \( x \)-axis. See Figure 51 (The plate must be concidered as infinitesimal thin, with infinite extent in th \( x \)-directions.) We are interested in finding the velocity field \( u(y,t) \) which developes because of the adherence between the fluid and the plate. The equation of motion for the problem may be stated as: $$ \begin{align} \rho \frac{\partial u}{\partial t} = \frac{\partial \tau_{xy}}{\partial y} \tag{3.152} \end{align} $$
The relation between the shear stress \( \tau_{xy} \) and the velocitygradient \( \frac{\partial u}{\partial y} \) is given by: $$ \begin{align} \tau_{xy} = K \cdot \left| \frac{\partial u}{\partial y} \right|^{\frac{1}{2}} \frac{\partial u}{\partial y} \tag{3.153} \end{align} $$
where \( K \) is a positive constant.
We introduce the following transformation which reduces the system to an ordinary differential equation: $$ \begin{align} \eta = C \cdot \frac{y}{t^{\frac{2}{5}}}, \quad f(\eta) = \frac{u}{U_0} \tag{3.154} \end{align} $$
where \( C \) is a positive constant, \( y \geq 0 \) and \( t \geq 0 \). By inserting equation (3.153) into equation (3.152) and using (3.154), we get: $$ \begin{align} f''(\eta) + 2 \, \eta \sqrt{f'(\eta)} = 0 \tag{3.155} \end{align} $$
With boundaryconditions: $$ \begin{align} f(0) = 0, f(\delta) = 1 \tag{3.156} \end{align} $$
where \( \delta \) is the boundary-layer thickness.
Pen and paper:
The following problems should be done using pen and paper:
a) We are first gonna solve equation (3.155) as an initial-value problem. In this problem we thus set \( f'(0)=1.25 \). Calculate \( f \), and \( f' \) for \( \eta=0.6 \) using Euler's method. Use \( \Delta \eta = 0.2 \)
b) Write Eq (3.155) as a system of equations. Explain how you could solve the problem using shooting technique, when \( f(0)=0 \), \( f(\delta)=1 \), and \( \delta \) is considered known.
c) During the solution of the system above we find that \( f'(\delta)=0 \). This information makes it possible to determine \( \delta \) as a part of the solution of the system in b). Explain how.
d) Solve equation (3.155) when \( f_1(0)=f'(0) \) is given. Show that the boundary condition \( f(\delta)=1 \) give \( f_1(0)= \frac{225}{128}=1.25311 \dots \)
Programming:
Write a python program that solves the problem defined in b. Use the information about \( \delta \) obtained in c.
Pen and paper:
a) Solutions: \( f(0.6)=0.732 \), \( f'(0.6)=0.988 \).
c) Perform the differentiation \( \frac{d}{d \eta} \left[ \sqrt{f'(\eta)}\right] \), and integrate equation (3.155) once. Solution: \( \delta=\sqrt{2 \sqrt{f'(0)}} \)
Programming:
You may use the template script below:
# src-ch2/stokes.py;ODEschemes.py @ git@lrhgit/tkt4140/src/src-ch2/ODEschemes.py;
#import matplotlib; matplotlib.use('Qt4Agg')
import matplotlib.pylab as plt
#plt.get_current_fig_manager().window.raise_()
import numpy as np
from ODEschemes import euler, heun, rk4
from math import sqrt
from scipy.interpolate import splev, splrep
#### set default plot values: ####
LNWDT=2; FNT=15
plt.rcParams['lines.linewidth'] = LNWDT; plt.rcParams['font.size'] = FNT
#### a: ####
def func(f, eta):
f0 = f[0]
f1 = f[1]
if f1<0:
# f1 should not be negative
f1=0
df0 = ?
df1 = ?
dF = np.array([df0, df1])
return dF
N = 5
Eta = np.linspace(0, 1, N + 1)
d_eta = Eta[1] - Eta[0]
f_0 = ?
df_0 = ?
F_0 = [f_0, df_0]
F = euler(func, F_0, Eta)
print "f(0.6) = {0}, f'(0.6) = {1}".format(F[N*3/5, 0], F[N*3/5, 1])
#### b/c: ####
N = 100 # using more gridpoints
d_eta = Eta[1] - Eta[0]
f_0 = 0
s0, s1 = 1., 1.1
delta = ?
Eta = np.linspace(0, delta, N + 1)
F_0 = [?, ?]
F = euler(func, F_0, Eta)
phi0 = ?
# Solve using shooting technique:
for n in range(4):
F_0 = [?, ?]
delta = ?
Eta = np.linspace(0, delta, N + 1)
F = euler(func, F_0, Eta)
phi1 = ?
s = ?
s1, s0 = s, s1
print "n = {0}, s = {1}, ds = {2}, delta = {3} ".format(n, s0, s1 - s0, delta)
# Transform to time-space variables:
C = 1.
U0 = 1
dt = 0.05
t0, tend = dt, 2.
dy = 0.01
y0, yend = 0, 2.
time = np.arange(dt, tend + dt, dt)
Y = np.arange(y0, yend + dy, dy)
Usolutions = np.zeros((len(time), len(Y)))
f = F[:, 0]*U0
tck = splrep(Eta, f) # create interpolation splines
for n, t in enumerate(time):
Eta_n = C*Y/(t**(2./5))
Eta_n = np.where(Eta_n>delta, delta, Eta_n) # if eta>delta set eta to delta
Usolutions[n, :] = splev(Eta_n, tck)
from Visualization import myAnimation
myAnimation(Y, Usolutions, time)
You also need this file in order to run simulation:
# src-ch2/Visualization.py
import matplotlib.pylab as plt
import numpy as np
from matplotlib import animation
def myAnimation(Y, Usolutions, time):
fig = plt.figure()
ax = plt.axes(xlim=(0, 1.1), ylim=(0, Y[-1]))
lines=[] # list for plot lines for solvers and analytical solutions
legends=[] # list for legends for solvers and analytical solutions
line, = ax.plot([], [])
time_text = ax.text(0.1, 0.95, '', transform=ax.transAxes)
dt = time[1]-time[0]
plt.xlabel('u')
plt.ylabel('y')
# initialization function: plot the background of each frame
def init():
time_text.set_text('')
line.set_data([], [])
return lines,
# animation function. This is called sequentially
def animate(i):
time = i*dt
time_text.set_text('time = %.4f' % time)
U = Usolutions[i, :]
line.set_data(U, Y)
return lines,
# call the animator. blit=True means only re-draw the parts that have changed.
anim = animation.FuncAnimation(fig, animate, frames=len(time), init_func=init, blit=False)
# Writer = animation.writers['ffmpeg']
# writer = Writer(fps=15, metadata=dict(artist='Me'), bitrate=1800)
# anim.save('../mov/stokes.mov', writer=writer)
plt.show()
Exercise 6: The Falkner-Skan equation
Blasius equation is a special case of a more general equation called the Falkner-Skan equation. The Falkner-Skan Transformation (1930) allows to write the original equation in a similarity form given by: $$ \begin{equation} f'''+ff''+\beta\cdot[1-(f')^2]=0. \tag{3.157} \end{equation} $$
It can be shown that the velocity \( U(x) \) is defined as: $$ \begin{equation} U(x)=U_0x^m,\ m= \text{constant}. \tag{3.158} \end{equation} $$
(3.157) is sometimes called the wedge flow equation because parameter \( \beta \) has the geometric meaning as shown in Figure 52:
Figure 52: Schematic representation of the Falkner-Skan equation reference frame and problem setup.
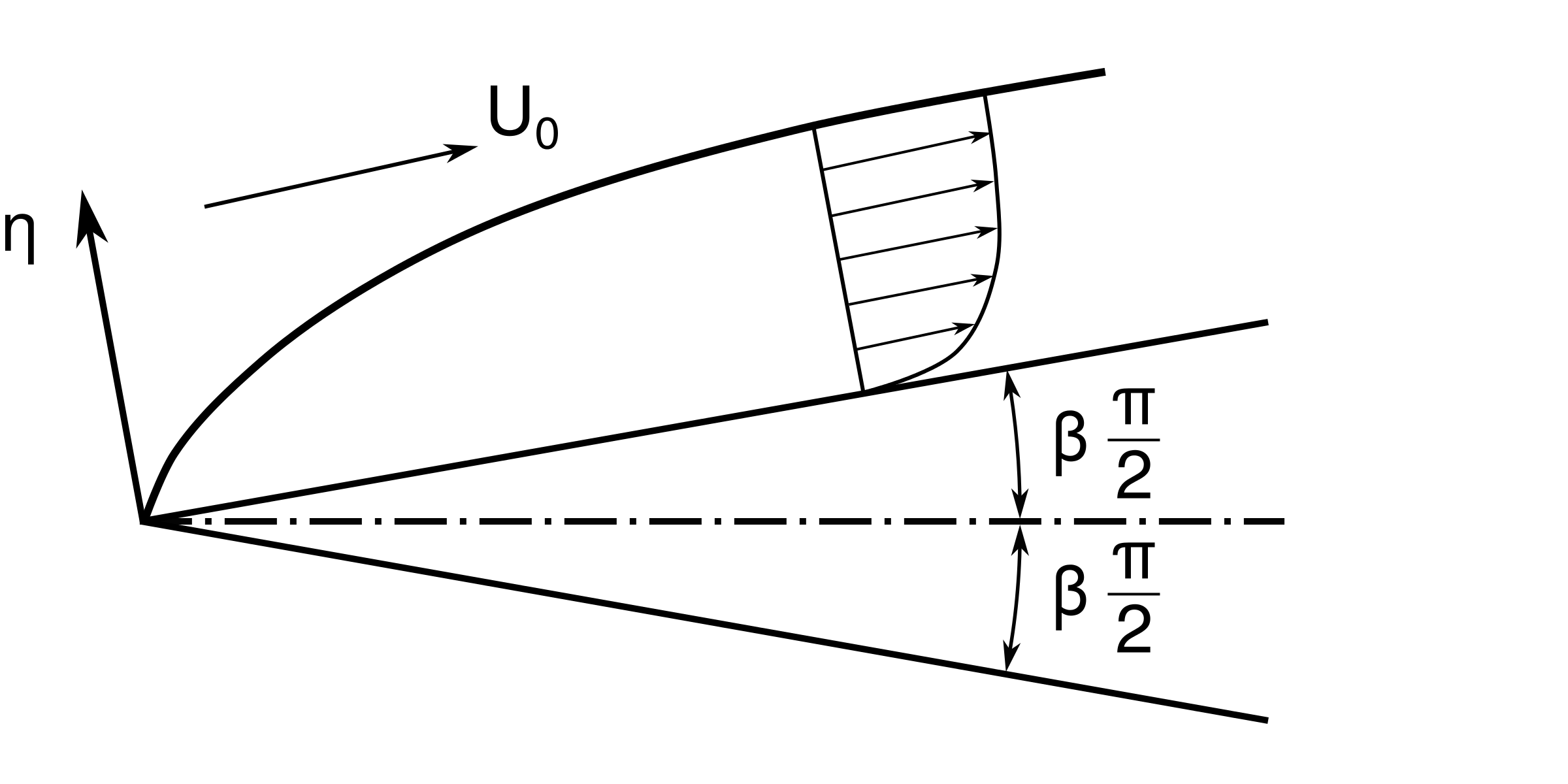
We see that half the wedge angle is \( \beta\cdot \frac{\pi}{2} \). For \( \beta=0 \), we get a flat plate and (3.157) becomes Blasius equation.
A detailed derivation can be found in Appendix C.3 in the Numeriske Beregninger. Here we reproduce some of the derivations for the sake of completeness.
Connection between \( m \) and \( \beta \): \( \beta=\frac{2m}{m+1} \) and \( m=\frac{\beta}{2-\beta} \). We see that \( \beta=0 \) results in \( U(x)=U_0 \).
Falkner-Skan transformation is given by: $$ \begin{equation} \eta=\sqrt{ \frac{U}{(2-\beta)\nu x} }\cdot y,\ f(\eta)=\frac{\psi}{\sqrt{(2-\beta)U\nu x}}, \tag{3.159} \end{equation} $$
where \( \psi \) is a potential function such that $$ \begin{equation*} u = \frac{\partial \psi}{\partial y}, \,\, v = \frac{\partial \psi}{\partial x} \end{equation*} $$
If we choose the same boundary conditions as in the example (3.3.3 Example: The Blasius equation), we get: $$ \begin{equation} f'''+ff''+\beta\cdot [1-(f')^2]=0, \tag{3.160} \end{equation} $$
with boundary conditions: $$ \begin{equation} \tag{3.161} \left.\begin{matrix} &f(0)=f'(0)=0, \\ &f'(\eta_\infty)=1. \end{matrix}\right.\ \end{equation} $$