7.5 Some numerical schemes for parabolic equations
7.5.1 Richardson scheme (1910)
The FTCS scheme is 1st order accurate in time and 2nd order accurate in space. We would like to have a scheme that is also 2nd order accurate in time. This can be achieved by using central finite differences for \( \frac{\partial u}{\partial t} \): $$ \begin{equation*} \frac{\partial u }{\partial t}\bigg |^n_j\approx \frac{u^{n+1}_j-u_j^{n-1}}{2\Delta t} \end{equation*} $$
which results in: $$ \begin{equation} \tag{7.57} u^{n+1}_j=u^{n-1}_j+2D\left( u^n_{j-1} -2u^n_{j}+u^n_{j+1} \right) \end{equation} $$
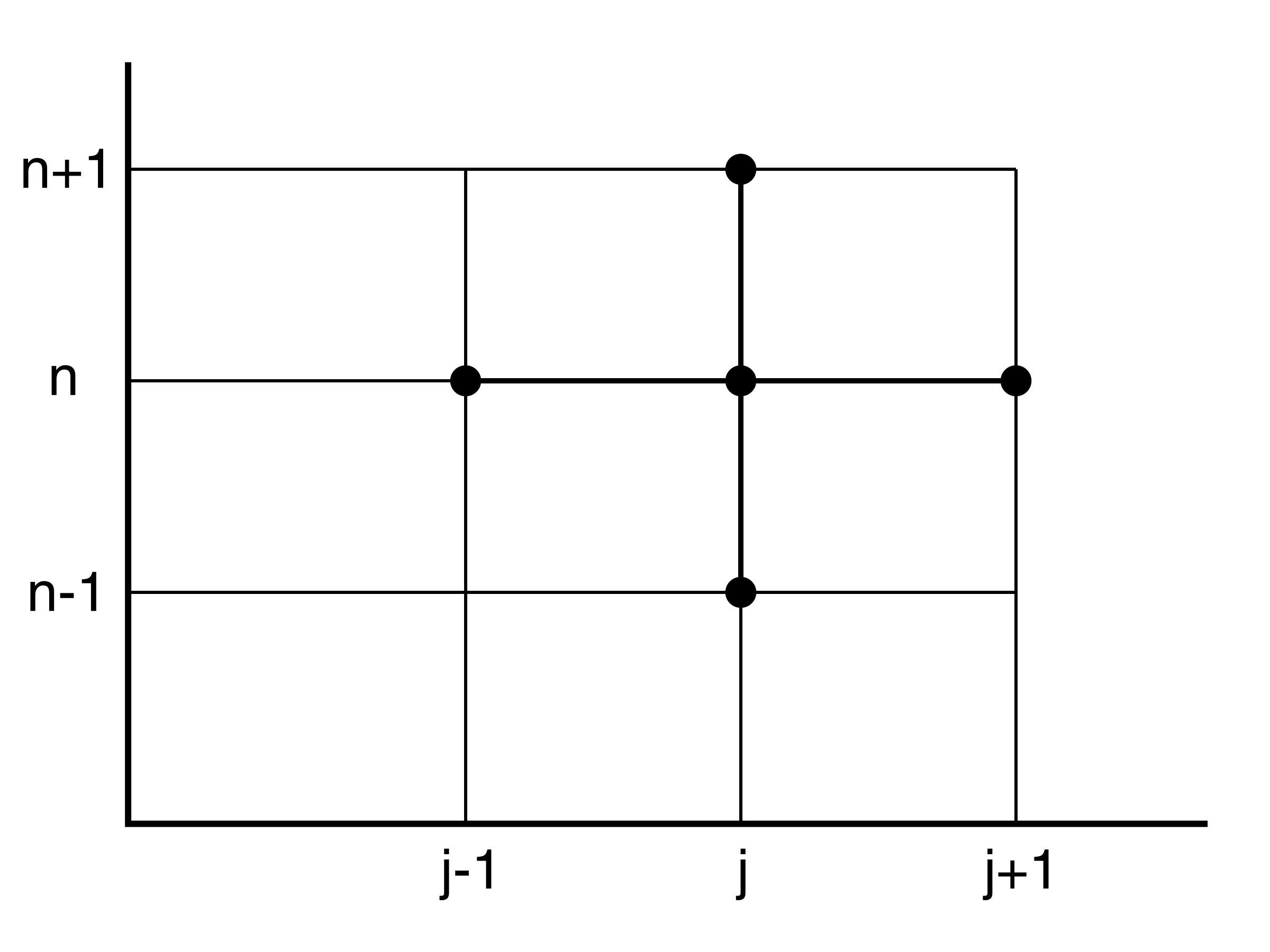
This is an explicit, 3-level scheme called Richardson scheme; see Figure 92.
Figure 92: 3-level stencil of the Richardson scheme (7.57).
Stability analysis
Let us first try with the criterion of positive coefficients introduced in (7.21). This condition can not be fulfilled for the coefficient in front of \( u^n_j \) for \( D > 0 \). Next, we try to gain insight on the stability of the scheme by using von Neumann's method. (7.42) inserted in (7.57) gives: $$ \begin{equation*} G^{n+1}e^{i\cdot \beta y_j} = G^{n-1}e^{i\cdot \beta y_{j}}+2D[G^ne^{i\cdot \beta y_{j-1}}-2G^ne^{i\cdot \beta y_j}+G^ne^{i\cdot \beta y_{j+1}}] \end{equation*} $$
Dividing with \( G^{n-1}e^{i\beta y_j} \) where \( y_j=j\cdot h: \) $$ \begin{equation*} \begin{array}{ll} G^2 & = 1+2DG\cdot \left(e^{-i\delta}+e^{i\delta}-2\right)=1+4DG\cdot(\cos(\delta)-1)\\ & = 1-8GD\cdot\sin^2\left(\frac{\delta}{2}\right) \end{array} \end{equation*} $$ where we have used (7.49) and (7.50). We have obtained a 2nd order equation because we are dealing with a 3-level scheme: $$ \begin{equation*} \begin{array}{l} G^2+2bG-1=0 \text{ med løsning}\\ G_{1,2}=-b\pm \sqrt{b^2+1},\ b=4D\sin^2\left(\frac{\delta}{2}\right)\geq0 \end{array} \end{equation*} $$
\( |G|=1 \) for \( b =0 \). For all other values of \( b \) we have that \( |G_2|>1 \). The scheme is therefore unstable for all actual values of \( D \). Such schemes are said to be unconditionally unstable. This example also shows that stability and accuracy can be rather independent concepts depending on how they are defined.
Use of derivation
We can also use derivation here: $$ \begin{equation*} \begin{array}{l} G^2=1+4DG\cdot (\cos(\delta)-1),\\ 2G\frac{dG}{d\delta}=4D\left[ (\cos(\delta)-1)\frac{dG}{d\delta}-G\sin(\delta) \right], \end{array} \end{equation*} $$ that with \( \frac{dG}{d\delta}=0 \) gives max-min for \( \delta=0 \), \( \delta=\pm \pi \), as for the FTCS scheme. For \( \delta = 0 \) we have \( G_{1,2}=\pm 1 \), while \( \delta = \pm \pi \), resulting in $$ \begin{equation*} G_{1,2}=-4D\pm \sqrt{1+(4D)^2} \end{equation*} $$
with instability for \( |G_2|>1 \) as before.