3.4 Shooting method for linear ODEs with two unknown initial conditions
In the follwing we will extend the shoothing methods we we derived in (3.1 Shooting methods for boundary value problems with linear ODEs) to problems with two initial conditions.
For such problemsn we must guess to initial values \( r \) and \( s \) with the corresponding boundary value error functions \( \phi \) og \( \psi \), respectively.
Figure 48: The boundary value error functions for boundary value problems with two unknown initial conditions.

As the ODE to be solved is linear, we know that the resulting boundary value error functions also will be linear. As \( \phi \) and \( \psi \) will be functions of the two initial guesses \( r \) and \( s \), the will express two planes which may be represented: $$ \begin{equation} \tag{3.130} \left.\begin{matrix} &\phi=A\cdot s+B\cdot r +C \\ &\psi=D\cdot s+E\cdot r+F \end{matrix}\right.\ \end{equation} $$
where \( A,B,C,\cdots,F \) are constants to be determined. The correct values \( r^* \) og \( s^* \) satisfy \( \phi(r^*,s^*)=0 \) and \( \psi(r^*,s^*)=0 \). (See Figure 48.)
Consequently we have six constants which may be found from the equations; three equations for \( \phi \): $$ \begin{align} &\phi^0=A\cdot s^0+B\cdot r^0+C \nonumber \\ &\phi^1=A\cdot s^1+B\cdot r^1+C \tag{3.131} \\ &\phi^{(2)}=A\cdot s^{(2)}+B\cdot r^{(2)}+C \nonumber \end{align} $$
and three equations for \( \psi \): $$ \begin{align} &\psi^0=D\cdot s^0+E\cdot r^0+F \nonumber \\ &\psi^1=D\cdot s^1+E\cdot r^1+F \tag{3.132} \\ &\psi^{(2)}=D\cdot s^{(2)}+E\cdot r^{(2)}+F \nonumber \end{align} $$
where \( s^0,\ s^1,\ s^{(2)},\ r^0,\ r^1 \) og \( r^{(2)} \) are initial guesses for the unknown initial values. For convenience we choose the following pairs of initial guesses: $$ \begin{align} s^0=0, & \qquad r^0=0 \nonumber \\ s^1=0, & \qquad r^1=1 \tag{3.133} \\ s^{(2)}=1, & \qquad r^{(2)}=0 \nonumber \end{align} $$
which results in the following expressions for the constants: $$ \begin{equation} \left.\begin{matrix} A=\phi^{(2)}-\phi^0, & B=\phi^1-\phi^0, & C=\phi^0, \\ D=\psi^{(2)}-\psi^0, & E=\psi^1-\psi^0, & F=\psi^0 \end{matrix}\right.\ \tag{3.134} \end{equation} $$
The correct values \( r^* \) og \( s^* \) which satisfies \( \phi(r^*,\ s^*)=0 \) and \( \psi(r^*,\ s^*)=0 \), i.e. \( A\cdot s^*+B\cdot r^*+C=D\cdot s^*+E\cdot r^*+C=0 \) may be expressed by the coefficients: $$ \begin{equation} s^*=\frac{E\cdot C-B\cdot F}{D\cdot B-A\cdot E},\qquad r^*=\frac{A\cdot F-D\cdot C}{D\cdot B-A\cdot E} \tag{3.135} \end{equation} $$
which after substitution of \( A,B,C,\dots,F \) results in: $$ \begin{align} s^* & =\frac{\psi^1\cdot\phi^0-\phi^1\cdot\psi^0}{(\psi^{(2)}-\psi^0)\cdot(\phi^1-\phi^0)-(\phi^{(2)}-\phi^0)\cdot(\psi^1-\psi^0)} \nonumber \\ \tag{3.136} \\ r^* & =\frac{\phi^{(2)}\cdot\psi^0-\psi^{(2)}\cdot\phi^0}{(\psi^{(2)}-\psi^0)\cdot(\phi^1-\phi^0)-(\phi^{(2)}-\phi^0)\cdot(\psi^1-\psi^0)} \nonumber \end{align} $$
The shooting method solution procedure for a linear ODE boundary value problem with two initial guesses then becomes:
We will illustrate the usage of this procedure in example (3.4.1 Example: Liquid in a cylindrical container).
3.4.1 Example: Liquid in a cylindrical container
In this example we consider a cylindrical container filled with a liquid to the height \( H \) for two different geometries, namely constant container wall thickness and with a container with at wall thickness which varies linearly (See Figure 49). We will look at the two geometries separately below.
3.4.1.1 Constant wall thickness
We denote radial displacement with \( W \). In the zoomed in part of Figure 49, \( V \) denotes shear force per unit length while \( M \) denotes moment per unit length.
Figure 49: A cylindrical container with a liquid of heigth \( H \). The arrows denote positive direction.
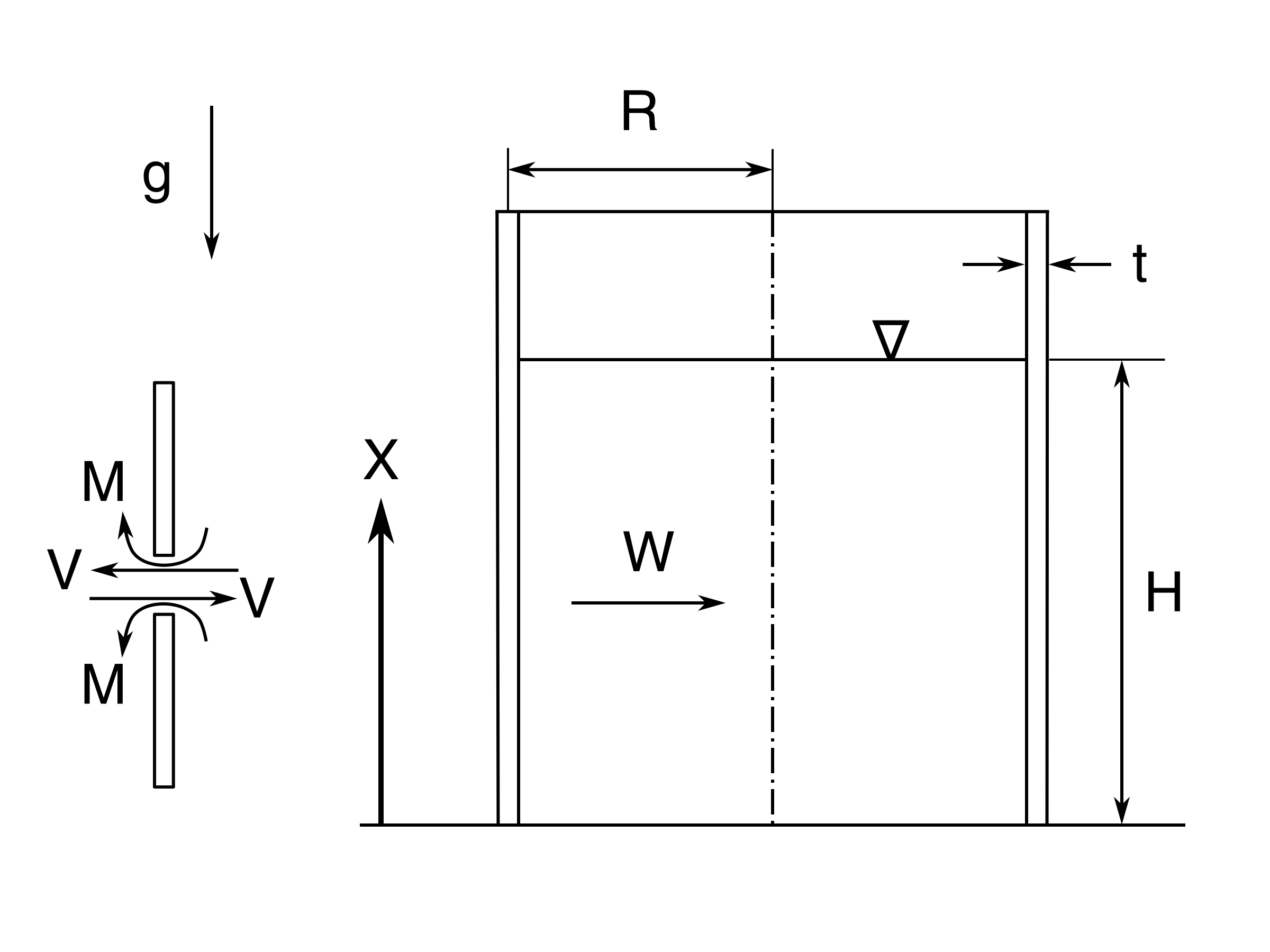
The differential equation for the displacement \( W \) is given by: $$ \begin{equation} \frac{d^4W}{dX^4}+B\cdot W=-\gamma \frac{H-X}{D} \tag{3.137} \end{equation} $$
where: $$ B=\dfrac{12(1-\nu^2)}{R^2t^2},\qquad D=\dfrac{Et^3}{12(1-\nu^2)},\qquad \gamma=\rho g $$
and \( \nu \) is Poisson's ratio, \( E \) the E-modulus and \( \rho \) the density of the fluid. For convenience we introduce dimensionless variables: $$ \begin{equation} x=\frac{X}{H} \qquad \text{and} \qquad w=\frac{E}{\gamma Ht}\, \left(\frac{t}{R}\right)^2 \, W \tag{3.138} \end{equation} $$
which after substitution in equation (3.137) results in the following dimensionless, fourth order ODE: $$ \begin{equation} \frac{d^4w}{dx^4}+4 \, \beta^4 \, w=-4 \, \beta^4 \, (1-x) \qquad \text{where} \qquad \beta^4=\frac{3(1-\nu^2)H^4}{R^2t^2} \tag{3.139} \end{equation} $$
Boundary conditions
To solve the ODE in equation (3.139) we need to supply some boundary conditions at both ends. At \( x= 0 \): $$ \begin{equation*} W=0,\ \qquad \text{and} \qquad \frac{dW}{dX}=0\ \text{(fixed beam)} \end{equation*} $$
At the other end, for \( X=H \) both the moment and the shear force must be zero, which mathematically corresponds to: $$ \begin{equation*} M=-D \frac{d^2W}{dX^2}=0,\ V=-D \frac{d^3W}{dX^3}=0 \end{equation*} $$
The dimensionless expression for the moment is \( m(x)=-\dfrac{d^2w}{dx^2} \), while the dimemsionless shear force has the expression: \( v(x)=-\dfrac{d^3w}{dx^3} \).
In dimensionless variables the boundary conditions takes the form: $$ \begin{align} w=0, \qquad \frac{dw}{dx}=0 \qquad \text{for} \quad x=0 \tag{3.140}\\ \frac{d^2w}{dx^2}=0, \qquad \frac{d^3w}{dx^3}=0 \qquad \text{for} \quad x=1 \tag{3.141} \end{align} $$
For our example we select a container with the following dimensions \( R=8.5m \), \( H=7.95m \), \( t=0.35m \), \( \gamma=9810N/m^3 \) (water), \( \nu=0.2 \), and the E-modulus \( E=2\cdot 10^4\text{MPa} \). For these values the nondimensional parameter \( \beta=6.0044 \).
Numerical solution with the shooting method for two unknown initial values
First we need to reformulate the fourth order ODE in (3.139) as a system of first order ODEs by following the procedure outlined in 2.4 Reduction of Higher order Equations.
By using the following auxilliary variables \( w=y_0,\ w'=y_0'=y_1,\ w''=y_1'=y_2,\ w'''=y_2'=y_3 \) we may write (3.137) as a system of four, first order ODEs: $$ \begin{align} y_0'& = y_1 \nonumber \\ y_1'& = y_2 \nonumber\\ y_2'& = y_3 \tag{3.142} \\ y_3'& =- 4\beta^4(y_0 + 1 -x) \nonumber \end{align} $$
with the following boundary conditions: $$ \begin{equation} y_0(0)=0,\ y_1(0)=0,\ y_2(1)=0,\ y_3(1)=0 \tag{3.143} \end{equation} $$
We intend to solve the boundary value problem defined by equations (3.142) and (3.143) with a shooting method approach, i.e. we will use and intital value solver and guess the unknown initital values. The intention with the shooting method is to find the unknown initial values \( s=w''(0)=y_2(0) \) and \( r=w'''(0)=y_3(0) \) such that the boundary values \( y_2(1)=0 \) and \( y_3(1)=0 \).
We introduce the boundary value error function as \( \phi(r,s)=y_2(1;r,s) \) and \( \psi(r,s)=y_3(1;r,s) \) and the correct values for our intitial guesses \( r^* \) og \( s^* \) are found when \( \phi(r^*,s^*)=0 \).
To find the correct initial guesses \( s=w''(0)=y_2(0) \) and \( r=w'''(0) \) we do the following:
- Solve (3.142) three times, always with \( y_0(0) \) and \( y_1(0)=0 \). The values of \( r \) and \( s \) for each solution is taken from (3.133).
- Compute the correct values for \( r^* \) and \( s^* \) from (3.136).
# src-ch2/tank1.py;ODEschemes.py @ git@lrhgit/tkt4140/src/src-ch2/ODEschemes.py;
from ODEschemes import euler, heun, rk4
from numpy import cos, sin
import numpy as np
from matplotlib.pyplot import *
# change some default values to make plots more readable
LNWDT=3; FNT=11
rcParams['lines.linewidth'] = LNWDT; rcParams['font.size'] = FNT
font = {'size' : 16}; rc('font', **font)
def tank1(y, x):
"""Differential equation for the displacement w in a cylindrical tank with constant wall-thickness
Args:
y(array): an array containg w and its derivatives up to third order.
x(array): independent variable
Returns:
dydx(array): RHS of the system of first order differential equations
"""
dydx = np.zeros_like(y)
dydx[0] = y[1]
dydx[1] = y[2]
dydx[2] = y[3]
dydx[3] = -4*beta4*(y[0]+1-x)
return dydx
# === main program ===
R = 8.5 # Radius [m]
H = 7.95 # height [m]
t = 0.35 # thickness [m]
ny = 0.2 # poissons number
beta = H*(3*(1 - ny**2)/(R*t)**2)**0.25 # angle
beta4 = beta**4
N = 100
X = 1.0
x = np.linspace(0,X,N + 1)
solverList = [euler, heun, rk4]
solver = solverList[2]
#shoot:
s = np.array([0, 0, 1])
r = np.array([0, 1, 0])
phi = np.zeros(3)
psi = np.zeros(3)
# evaluate the boundary value error functions for the initial guesses in s and r
for k in range(3):
y0 = np.array([0, 0, s[k], r[k]])
y = solver(tank1, y0, x)
phi[k] = y[-1, 2]
psi[k]=y[-1, 3]
# calculate correct r and s
denominator = (psi[2] - psi[0])*(phi[1] - phi[0]) - (phi[2] - phi[0])*(psi[1] - psi[0])
rstar = (phi[2]*psi[0] - psi[2]*phi[0])/denominator
sstar = (psi[1]*phi[0] - phi[1]*psi[0])/denominator
print('rstar', rstar, 'sstar', sstar)
# compute the correct solution with the correct initial guesses
y0 = np.array([0, 0, sstar, rstar])
y = solver(tank1, y0, x)
legendList=[]
plot(x,-y[:,3]/beta**2)
plot(x,-y[:,2]/beta)
legendList.append(r'$v(x)/\beta^2$ ')
legendList.append(r'$m(x)/\beta$ ')
# Add the labels
legend(legendList,loc='best',frameon=False)
ylabel('v, m')
xlabel('x')
grid(b=True, which='both', color='0.65',linestyle='-')
#savefig('../figs/tank1.pdf')
show()
Note that the ODE in equation (3.139) may be classified as singular as the highest order derivative is multiplied with a potentially very small number \( \varepsilon=\frac{1}{4\beta^4} \), when rearranged. We observe that \( \varepsilon \to 0 \) as \( \beta\to\infty \) and that the nature of equation (3.139) will go from an ODE to an algebraic equation. The analytical solution may be shown to have terms of the kind \( e^{\beta x}\sin\beta x \) og \( e^{\beta x}\cos\beta x \) (see equation (D.1.6) and (D.1.8), part D.1, appendix D in Numeriske Beregninger.
3.4.1.2 Varying wall thickness
In the following we will modify the example above of liquid in a cylindrical container by allowing for a wall thickness which varies linearly from \( t_0 \) at the bottom to \( t_1 \) at the top.
Figure 50: A cylindrical container with a varying wall thickenss containing a liquid of heigth \( H \).
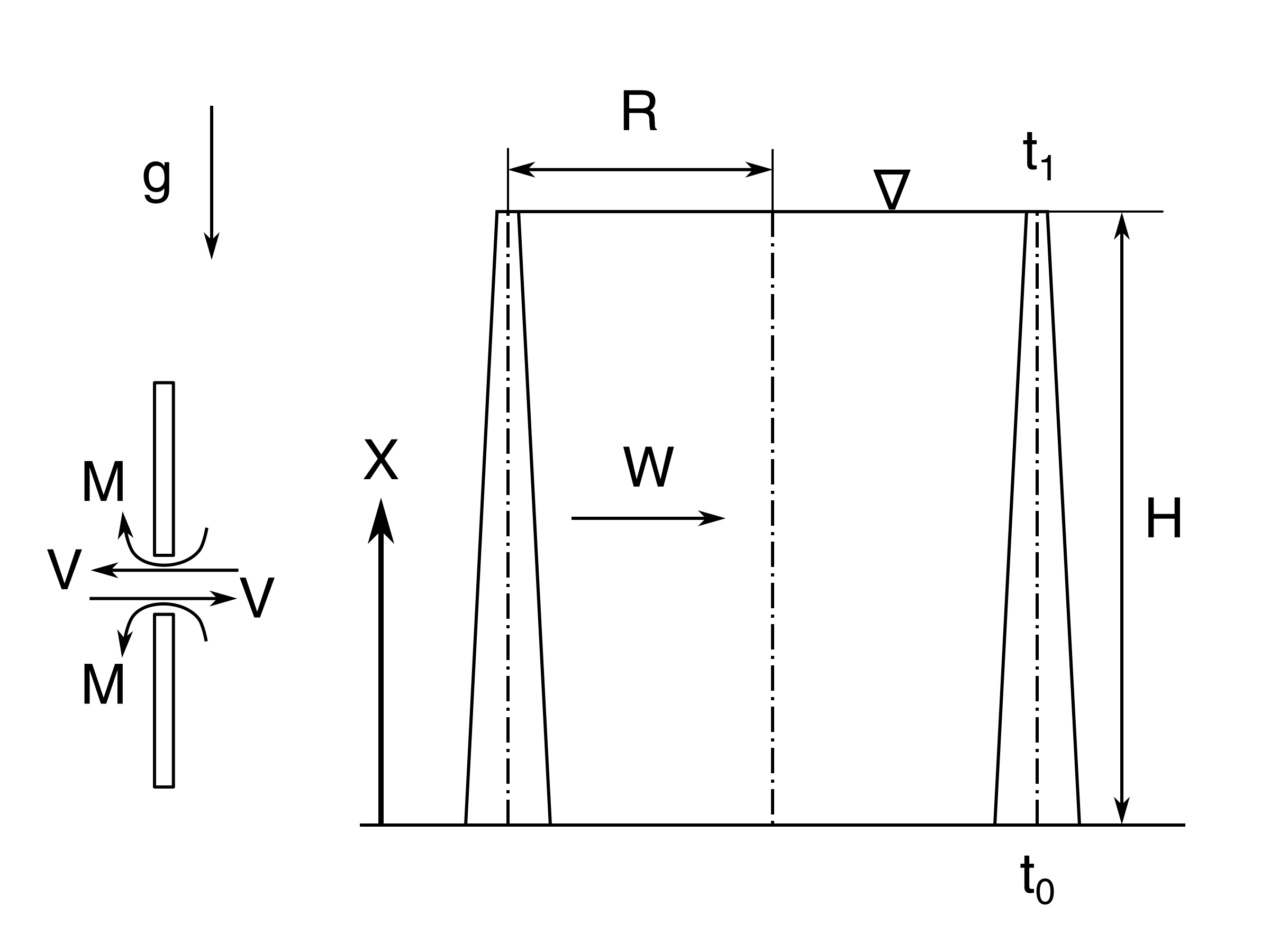
Based on \( t_0 \) and \( t_1 \), we introduce \( \alpha=\dfrac{t_0-t_1}{t_0} \) the steepness of the wall thickness, which allows for the thickness \( t \) to be represented as: $$ \begin{equation} t=\left(1-\alpha \frac{X}{H}\right)\cdot t_0,\ 0\leq X\leq H \tag{3.144} \end{equation} $$
The differential equaiton for the displacement \( W \) for this situation is given by: $$ \begin{equation} \frac{d^2}{dX^2}\left(D \frac{d^2W}{dX^2}\right)+E \frac{tW}{R^2}=-\gamma(H-X) \tag{3.145} \end{equation} $$
where \( D=\dfrac{Et^3}{12(1-\nu^2)},\ \gamma=\rho g \), with the same meaning as in the previous part of the example.
Dimensionless form $$ \begin{equation} x=\frac{X}{H},\quad w=\frac{E}{\gamma Ht_0}\left(\frac{t_0}{R}\right)^2 \; W,\quad \beta^4=\frac{3(1-\nu^2)}{R^2t_0^2} \; H^4 \tag{3.146} \end{equation} $$
By substitution of (3.146) in (3.145) we get the following nondimensional ODE: $$ \begin{equation} \frac{d^2}{dx^2}\left[ (1-\alpha x)^3\frac{d^2w}{dx^2}\right] +4\beta^4(1-\alpha x)\cdot w=-4\beta^4(1-x) \tag{3.147} \end{equation} $$
which may be differentiated to yield: $$ \begin{equation} \frac{d^4w(x)}{dx^4}-\frac{6\alpha}{(1-\alpha x)}\frac{d^5w(x)}{dx^5}+\frac{6\alpha^2}{(1-\alpha x)^2}\frac{d^2w(x)}{dx^2}+\frac{4\beta^4}{(1-\alpha x)^2}w(x)=-\frac{4\beta^4(1-x)}{(1-\alpha x)^5} \tag{3.148} \end{equation} $$
This problem has also an analytical, but more complicated, solution (see appendix D, part D.2 in Numeriske Beregninger) expressed by means of Kelvin functions, a particular kind of Bessel functions. However, the numerical solution remains the same as for the case with the constant wall thickness.
We choose physical parameters as for the previous example: $$ \begin{equation} \tag{3.149} \left.\begin{matrix} &R=8.5m,\ H=7.95m,\ t_0=0.35m ,\ t_1=0.1m \\ &\gamma=9810N/m^3\text{(vann)},\ \nu=0.2,\ E=2\cdot 10^4\text{MPa} \end{matrix}\right.\ \end{equation} $$
and \( \alpha=\frac{t_0-t_1}{t_0}=\frac{5}{7} \) and as previously we get \( \beta=6.0044 \).
Numerical solution
We proceed as before with \( w=y_0,\ w'=y_0'=y_1,\ w''=y_1'=y_2,\ w'''=y_2'=y_3,\ z=1-\alpha x \) and write (3.144) as a system of four first order ODEs: $$ \begin{align} y_0'& = y_1 \nonumber \\ y_1'& = y_2 \nonumber\\ y_2'& = y_3 \tag{3.150} \\ y_3'&=\frac{6\alpha}{z} \, y_3-\frac{6\alpha^2}{z^2} \, y_2-\frac{4\beta^4}{z^2} \, y_0-\frac{4\beta^4(1-x)}{z^3} \nonumber \end{align} $$
with the following boundary conditions: $$ \begin{equation} y_0(0)=0,\ y_1(0)=0,\ y_2(1)=0,\ y_3(1)=0 \tag{3.151} \end{equation} $$
Only the last equation in the system of ODEs (3.150) differs from the previous part of the example 3.4.1.1 Constant wall thickness).
The procedure will be as for 3.4.1.1 Constant wall thickness, except for the we now are introduced the additional parameter \( \alpha \).
# src-ch2/tank2.py;ODEschemes.py @ git@lrhgit/tkt4140/src/src-ch2/ODEschemes.py;
from ODEschemes import euler, heun, rk4
from numpy import cos, sin
import numpy as np
from matplotlib.pyplot import *
# change some default values to make plots more readable
LNWDT=3; FNT=11
rcParams['lines.linewidth'] = LNWDT; rcParams['font.size'] = FNT
font = {'size' : 16}; rc('font', **font)
def tank2(y, x):
"""Differential equation for the displacement w in a cylindrical tank with linearly varying wall-thickness
Args:
y(array): an array containg w and its derivatives up to third order.
x(array): independent variable
Returns:
dydx(array): RHS of the system of first order differential equations
"""
z = 1-alpha*x
dydx = np.zeros_like(y)
dydx[0] = y[1]
dydx[1] = y[2]
dydx[2] = y[3]
temp = (6*alpha/z)*y[3]- (6*alpha**2/z**2)*y[2]
dydx[3] = temp - 4*beta4*y[0]/z**2 - 4*beta4*(1-x)/z**3
return dydx
R = 8.5 # radius [m]
H = 7.95 # height [m]
t0 = 0.35 # thickness [m]
t1 = 0.1 # thickness [m]
ny = 0.2 # poissons number
beta = H*(3*(1-ny**2)/(R*t0)**2)**0.25
beta4 = beta**4
alpha = (t0-t1)/t0
N = 100
print("beta: ", beta, "alpha", alpha)
X = 1.0
x = np.linspace(0,X,N + 1)
solverList = [euler, heun, rk4] #list of solvers
solver = solverList[2] # select specific solver
# shoot:
s = np.array([0, 0, 1])
r = np.array([0, 1, 0])
phi = np.zeros(3)
psi = np.zeros(3)
for k in range(3):
y0 = np.array([0,0,s[k],r[k]])
y = solver(tank2,y0,x)
phi[k] = y[-1, 2]
psi[k]=y[-1, 3]
# calculate correct r and s
denominator = (psi[2] - psi[0])*(phi[1] - phi[0]) - (phi[2] - phi[0])*(psi[1] - psi[0])
rstar = (phi[2]*psi[0] - psi[2]*phi[0])/denominator
sstar = (psi[1]*phi[0] - phi[1]*psi[0])/denominator
print('rstar', rstar, 'sstar', sstar)
# compute the correct solution with the correct initial guesses
y0 = np.array([0, 0, sstar, rstar])
y = solver(tank2,y0,x)
legends=[] # empty list to append legends as plots are generated
plot(x,-y[:,3]/beta**2)
plot(x,-y[:,2]/beta)
legends.append(r'$v(x)/\beta^2$')
legends.append(r'$m(x)/\beta$')
# Add the labels
legend(legends,loc='best',frameon=False) # Add the legends
ylabel('v, m')
xlabel('x')
grid(b=True, which='both', color='0.65',linestyle='-')
show()