Example 2.2: Heat Equation in 2-D

We consider the linear heat equation in two spatial dimensions

$u_t = \Delta u = u_{xx} + u_{yy}, \qquad u(x,y,0)=u_0(x,y)$

The natural splitting method for this equation is to solve it dimension by dimension, that is, use the splitting

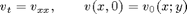
$v_t = v_{xx}, \qquad v(x,0) = v_0(x;y)$

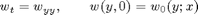
$w_t = w_{yy}, \qquad w(y,0) = w_0(y;x)$

To compute the solution of each of the 1-D problems, we will use a spectral method.

Initial setup

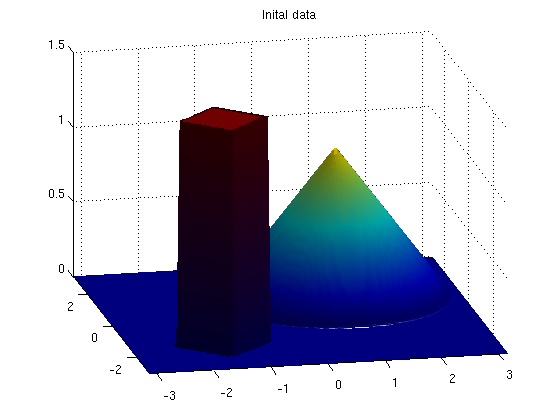
N     = 128;  % Number of grid points. NB, N must be even!
T     = 0.25; % Final time
dt    = T/6;  % Time step in splitting
x     = linspace(-pi,pi,N); y=x;
[X,Y] = meshgrid(x,y);
r1    = sqrt((X-1).^2+(Y-1).^2);
r2    = abs(X+1.5)+abs(Y+1.5);
u0    = max(0.0,1-0.5*r1) + 1.5*(r2<0.8);

surf(x,y,u0), axis([-pi pi -pi pi 0 1.5]),
shading interp; light, view(-12,24), title('Inital data')

Solving the equation by splitting

Nt=ceil(T/dt); dt=T/Nt;
u=zeros(length(x),length(y),Nt+1);
u(:,:,1)=u0;
for i=1:Nt,
	u1         = heat(u(:,:,i),dt,1);   % Diffusing in the x-direction
	u(:,:,i+1) = heat(u1,dt,2);         % Diffusing in the y-direction
end;

Plot final solution

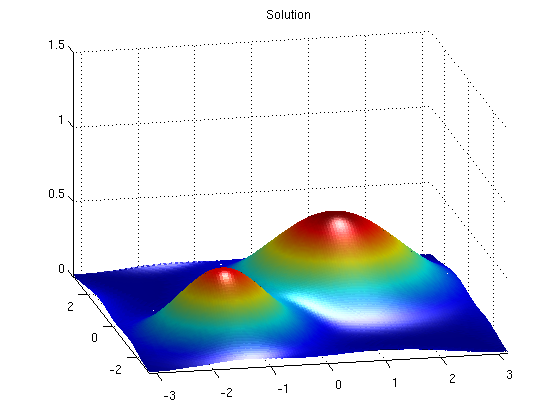
surf(x,y,u(:,:,Nt+1)); axis([-pi pi -pi pi 0 1.5])
shading interp; light, view(-12,24), title('Solution')