Rotation Demonstration: Discontinous Data

A demonstration of how the timestep affects the error of the splitting method for a rotation. Similar results can be expected in general, although nonlinear sharpening may give smaller errors.

The equation we solve is

$u_t - y u_x + x u_y = 0, \qquad u(x,y,0)=u_0(x,y)$

where the initial function u0 is discontinuous. To solve the equation, we will use Godunov splitting and front tracking to approximate the 1-D solution operators.

Initial setup

T     = 4*pi;
xmin  = -1.5; xmax=1.5;
N     = 128;
h     = (xmax-xmin)/N;
x     = xmin+h*(0:N);
y     = 0.5*(x(1:end-1)+x(2:end));
[X,Y] = meshgrid(y,y);
u0    = adiscontnuous_function(X,Y);
surfl(X,Y,u0); shading interp, view(-15,60), colormap(gray), axis tight

Error versus CFL number

First we study the pointwise and the L1 error for CFL numbers 2.^(0:5)

colormap(jet)
for i=1:6
	nu=2^(i-1);
	err= abs( rotrack(u0,y,y,nu,T) - u0);
   subplot(2,3,i), pcolor(y,y,err), axis equal image, shading interp;
   set(colorbar('West'),'XColor',[1 1 1],'YColor',[1 1 1]);
   caxis([0 2]), title(['CFL = ', num2str(nu)]);
   set(gca,'XTick',[],'YTick',[])
   xlabel(['L1 error: ', num2str(h*h*sum(abs(err(:))))]);
	drawnow;
end;

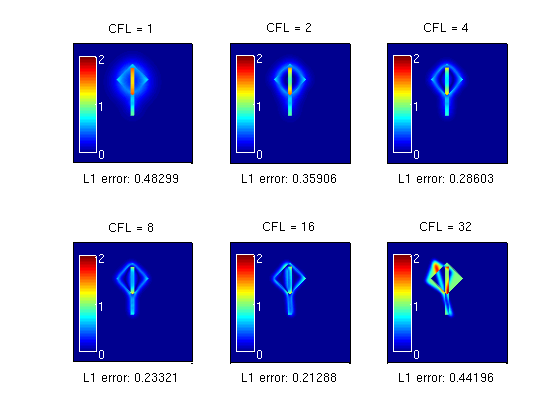
The error is determined by two error mechanisms that work in opposite directions. The splitting error increases with increasing splitting steps, whereas the smoothing error caused by the projection operator increases with decreasing splitting steps. The total splitting error is therefore a convex function of the time step, and in the figure above, the minimum error is observed for CFL number 16.

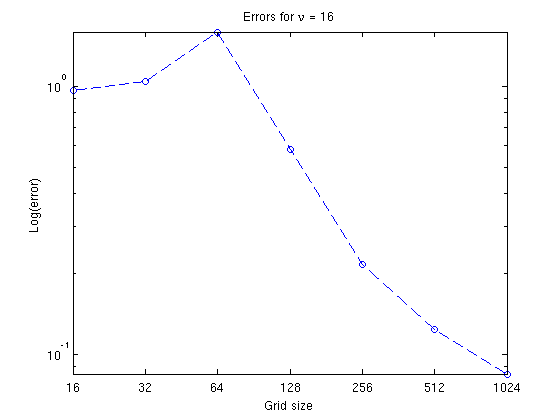
Testing convergence

We choose the best CFL number vu=16, and check for convergence rate. To this end, we use only one lap (it takes too long otherwise).

T    = 2*pi;
Lerr = zeros(1,7);
wbar = waitbar(0,'Convergence study');
for i=1:7,
	N    = 2^(i+3);
	h    = (xmax-xmin)/N; x=xmin+h*(1:N);
	[X,Y]=meshgrid(x,x);
	u0   = adiscontnuous_function(X,Y);
	err  = abs(rotrack(u0,x,x,nu,T) - u0);
	Lerr(i)=sum(err(:)) / sum(abs(u0(:)));
	waitbar(i/7,wbar);
end;
close(wbar);
clf, semilogy(1:7,Lerr,'o--');
set(gca,'XTick',1:7,'XTickLabel',2.^((1:7)+3))
xlabel('Grid size'); ylabel('Log(error)'); axis tight
title('Errors for \nu = 16');