Example 4.2: Splitting Step in a Viscous Splitting

We consider the viscous Burgers' equation

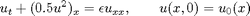
$u_t + (u^2)_x/2 = \epsilon u_{xx}, \qquad u(x,0)=u_0(x)$

Here \epsilon is a scaling parameter that gives the relative balance between advective and viscous forces. We consider the smooth initial data

$u_0(x) = -sin(\pi x), \quad x\in[-1,1]$

Approximate solutions will be constructed using a standard viscous splitting, in which the hyperbolic and the parabolic terms are solved for separately. To maximise computational efficiency, it is desirable to use as large splitting stpes as possible, especially when using a conditionally stable method for the hyperbolic equation.

Initial setup

xmin=-1.5; xmax=1.5; T=1.0;
epsilon=0.01;

Reference solution

To compute a reference solution, we a fine grid and set the number of splitting steps to be twice the number of grid points. This will effectively amount to an unsplit method.

N  = 2047;
h  = (xmax-xmin)/N;
x  = xmin+(0:N)*h; nstep=2*N;
u0 = -(abs(x)<=1.0).*sin(pi*x);
u  = diffBurg('iden',u0,epsilon,h,1,nstep,'neumann');
uref=u(:,nstep+1); xref=x;

Operator splitting solutions

We will compare two solutions computed on a grid with 75 grid points using one and sixteen splitting steps, respectively.

N  = 74;
h  = (xmax-xmin)/N;
x  = xmin+(0:N)*h;
u0 = -(abs(x)<=1.0).*sin(pi*x);

nstep = 1;
u  = diffBurg('iden',u0,epsilon,h,1,nstep,'neumann');
u1 = u(:,nstep+1);

nstep = 16;
u   = diffBurg('iden',u0,epsilon,h,1,nstep,'neumann');
u16 = u(:,nstep+1);

plot(xref,uref,x,u16,'-o',x,u1,'-*')
legend('reference', '1 step', '16 steps')

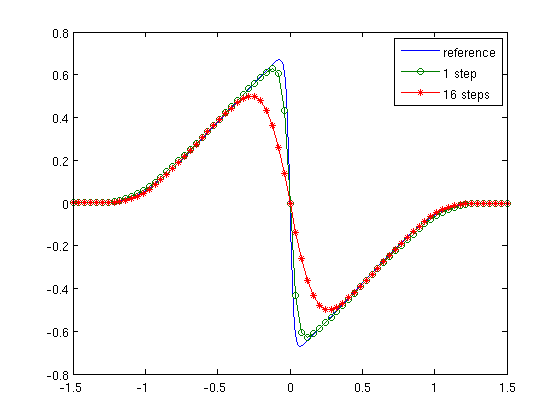
From the plot, we see that there is a significant difference between the two operator splitting solutions. The width of the physical shock layer is of the order O(\epsilon), whereas the width of the shock layer in an operator splitting approximation will typically be of the order O(\sqrt(k \epsilon) ), where k is the length of the splitting step. For the given choice of \epsilon, we have that 1/sqrt(\epsilon)=10, which indicates that we need of the order ten splitting steps to correctly resolve the shock layer. This is confirmed by the figure.