Example A.2: Burgers' Equation
In this example we will study Burgers' equation
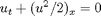
which is the archetypical example of a nonlinear equation, possessing a convex flux that may cause discontinuous shock waves to form even for smooth initial data. We assume Neumann boundary conditions and use a single shock as initial data.
For this particular setup, we know the exact solution
T = 1.2; NN = 512; hh=1/NN; xx=hh*(1:NN); uexact = 1.0*(xx<(0.1+0.5*T));
We then solve the equation numerically using two first-order methods (Lax-Friedrichs and the upwind method) and two second-order methods (Lax-Wendroff and MacCormack)
N = 32; h=1.2/N; x=h*(1:N);
u0 = 1.0*(x<0.1);
method = {'LxF', 'upwind', 'LxW', 'McC'};
name = {'Lax-Friedrichs', 'Upwind', 'Lax-Wendroff', 'MacCormack'};
for i=1:4
u=finvol('burgers',u0,T,h,1,'neumann',method{i},.9);
subplot(2,2,i);
plot(xx,uexact,'-',x,u,'o','MarkerSize',4); axis([0 1 -0.2 1.3]);
title(name{i});
end
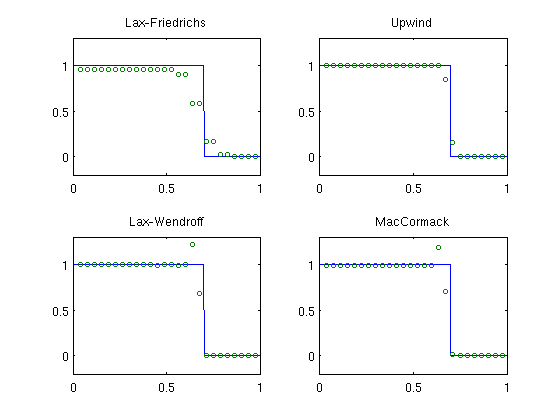
Comparing the two first-order schemes, we see that the upwind scheme resolves the discontinuity quite sharply, whereas the Lax–Friedrichs smears it out over several grid cells. Both second-order schemes resolve the discontinuity sharply, but produce spurious oscillations upstream.