Basic ultrasound

Basically, discrete objects with high reflexivity wil cause attenuation shadows, as shown below. However, the shadows are both due to the absorbtion in dense tissue, and of the reflection at the border zones, if they have a high reflexivity coefficient.

Shadowing and colouring

Behind organs with low density (reflexivity) on the other hand, the tissue appears brighter (colouring). This is simply lack of attenuation - acoustic enhancement.

Shadows

In echocardiography, the shadows may even be useful, as a clue to a high reflexivity of structures, meaning they are usually calcified (thick, dense stuctures may seem very bright in the usual scanner setting but will usually not cast a shadow if not calcified.:

Gain

Time gain compensation (TGC)

Compress and reject:

Angle dependency in distance and motion measurement

The angle dependency of Doppler measurements, is well known. However, M-mode measurements are just as angle dependent:

Thus, a skewed cross sectional M.mode will overestimate both wall thicknesses and chamber diameters.

The angle distortion is eliminated, however, by using ratios. Fractional shortening and wall thickening are ratios of diastolic values and systolic changes, where the overestimation is present in both diastole and systole (unless the angle changes during systole, of course), and the ratios will remain unchanged.Thus wall thickening and fractional shortening can be estimated even if the line is skewed.

However measuring absolute dimensions or motion by M-mode, will lead to an over estimation by M-mode just as in measuring distances:

Again measuring displacement relative to end diastolic wall length, will give correct values, as both wall length and displacement will have the same ratio despite the angulation error, if measured along the same straight line. Thus, global strain in not affected to the same degree.

Out of plane motion

The most common out of plane motion, is the movement of the base towards the apex, which is the longitudinal shortening of the ventricle. This is evident from the long axis view, but not the short axis:


Normal long axis image. The motion of the base of the ventricle towards the apex is evident in the long axis view.	Looking at the short axis view from the base, this is not evident, but comparing with the image on the left, this mus mean that during systole, an entirely new part of the ventricle moves into the imaging plane.

This, of course affects M-mode measurements as well:


As can be seen, the base of the heart moves through the M-mode line during the heart cycle.	This means that measurements in fact are taken from different part of the ventricle in end diastolie and end systole. It seems to indicate that systolic measurements are done in a part of the ventricle with narrower lumen and thicker wall, thus may over estimating both fractional shortening and wall thickening.

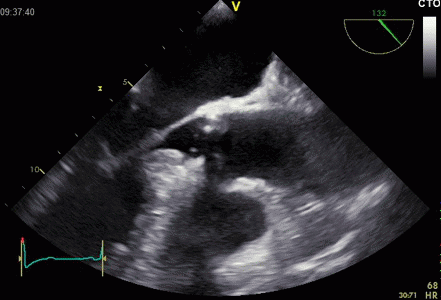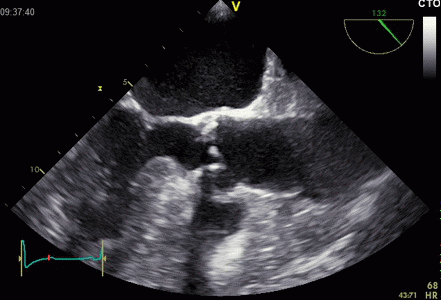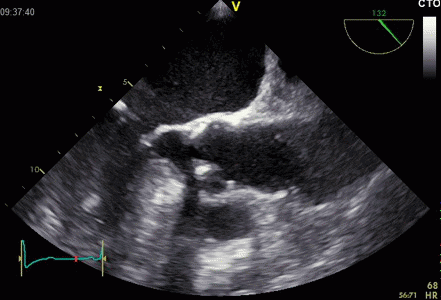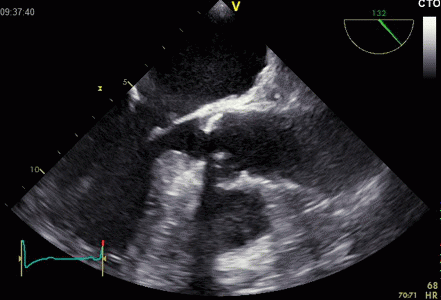
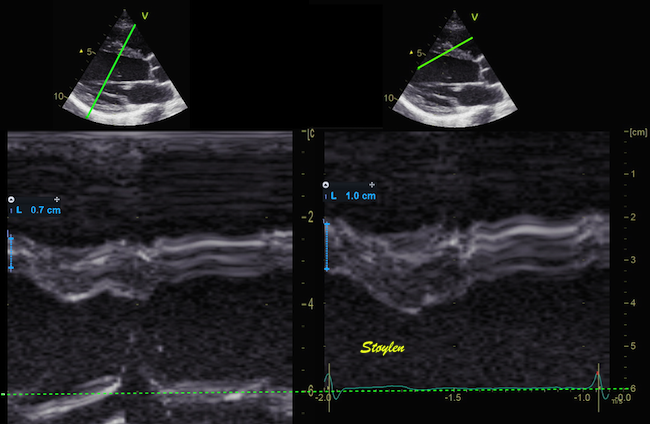
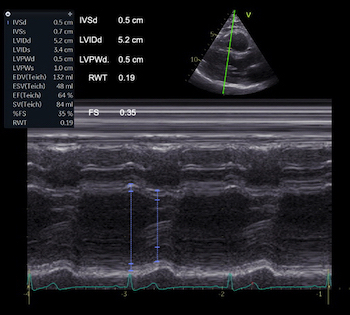
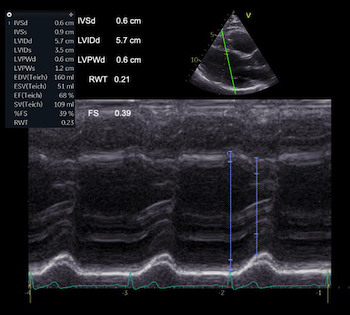
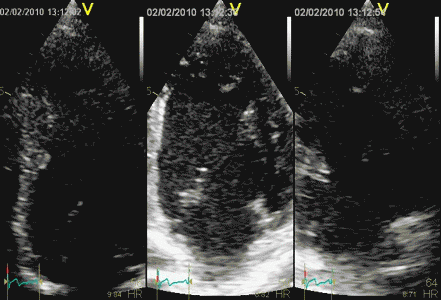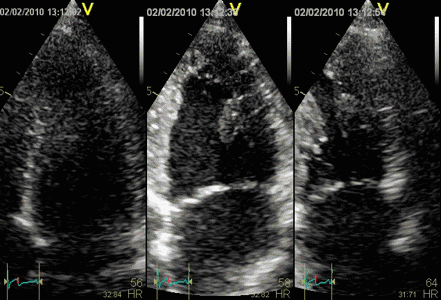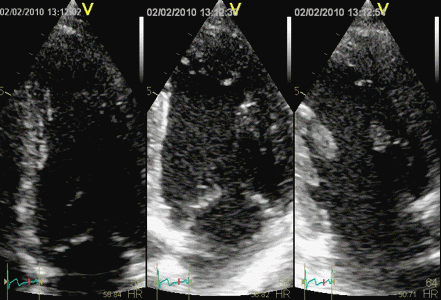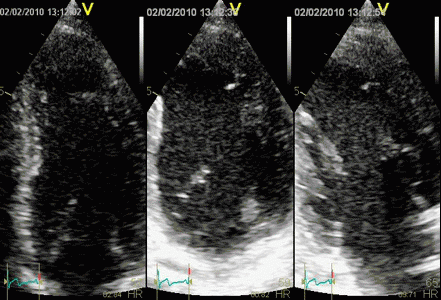
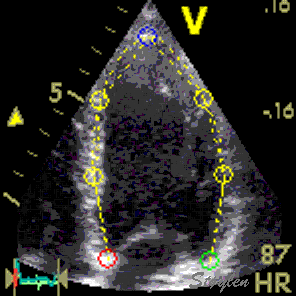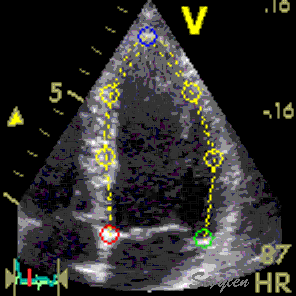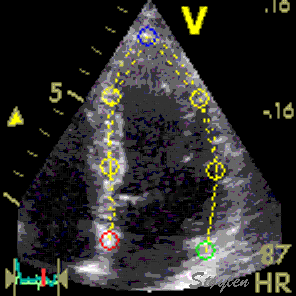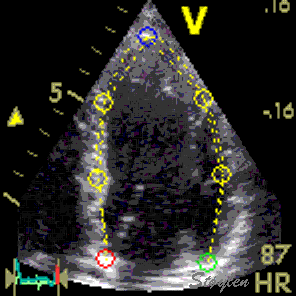
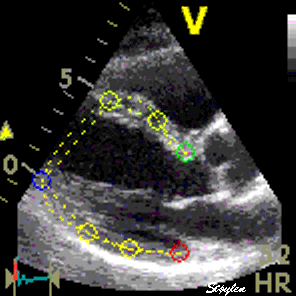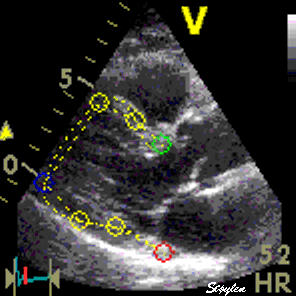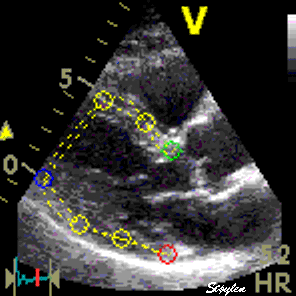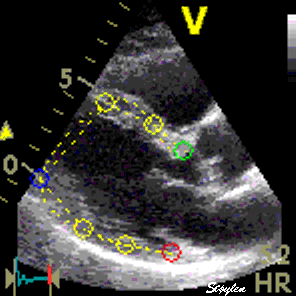
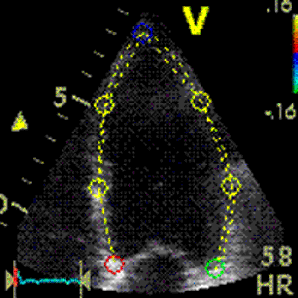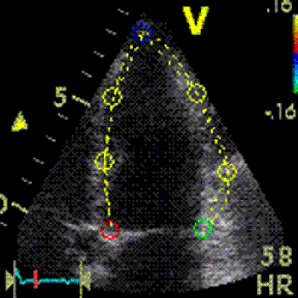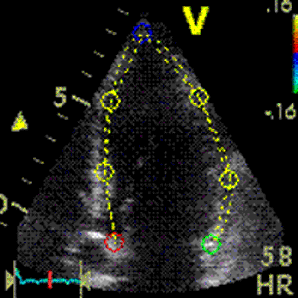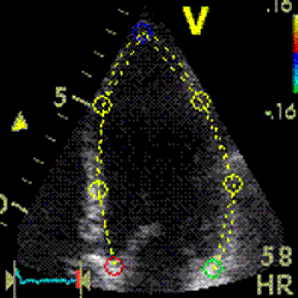
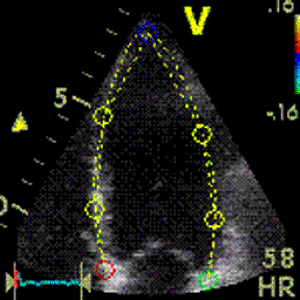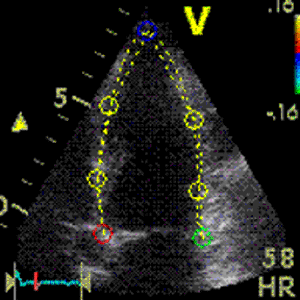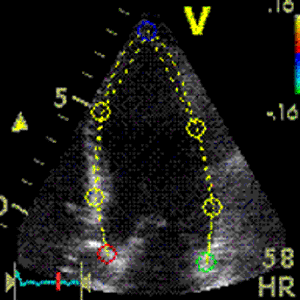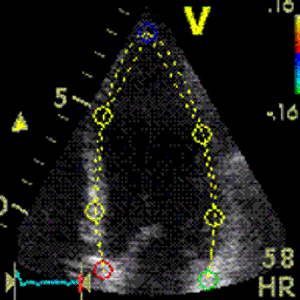
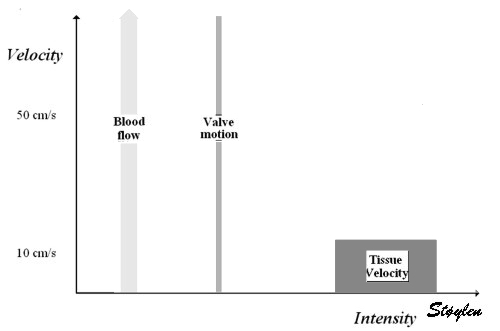
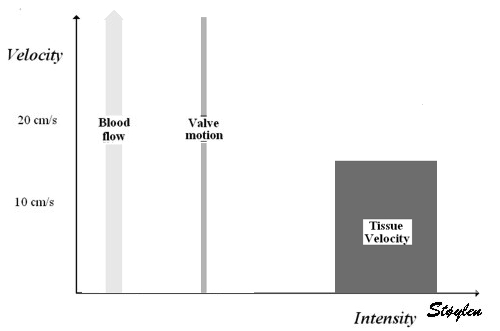
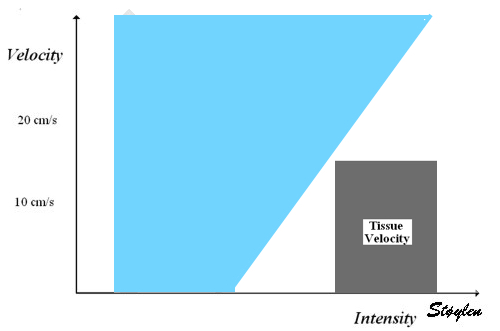
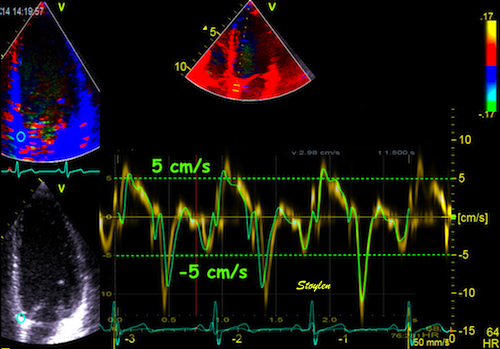
Interestingly, the M-mode values of HUNT3 showed a substantial higher wall thickening in the PW than in the septum, while the 2D measurements in HUNT 4 did not reproduce this finding. This effect is probably due to the specific vulnerability of M-mode to the effects of the long axis shortening, making the M-mode cress different parts of the LV in systole and diastole. The configuration of the posterior wall in then base may thus induce a statistical bias towards over estimation of wall thickness as shown below.

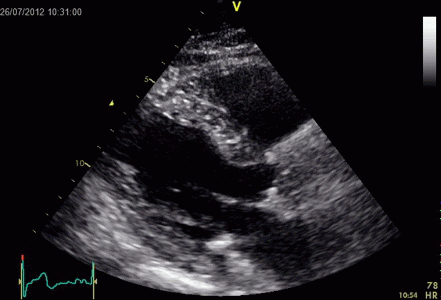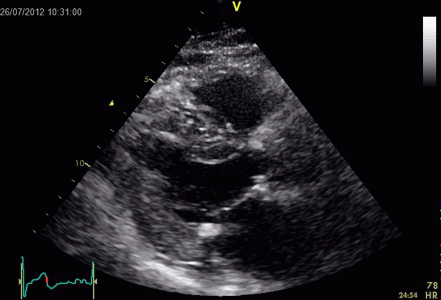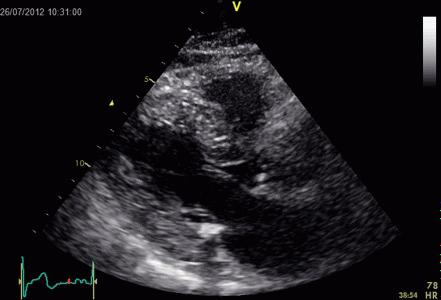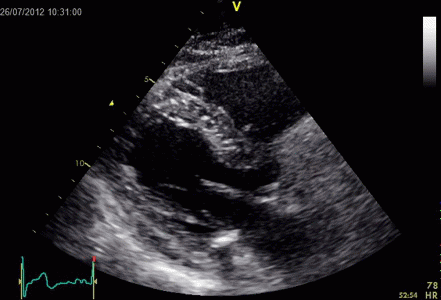
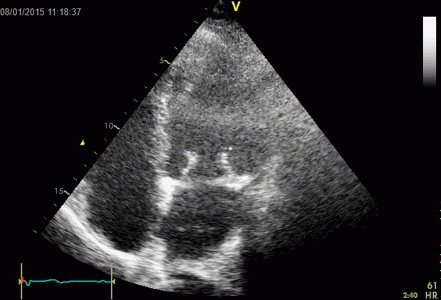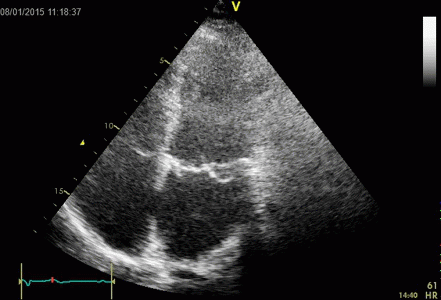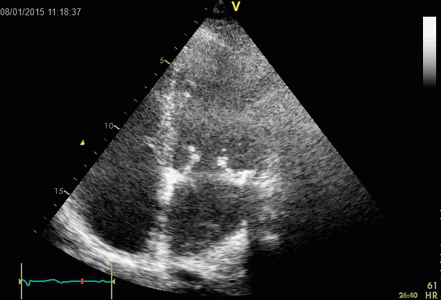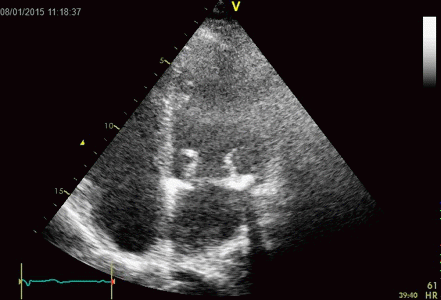
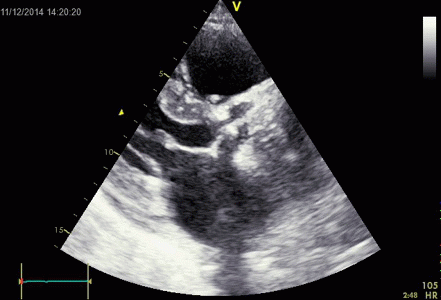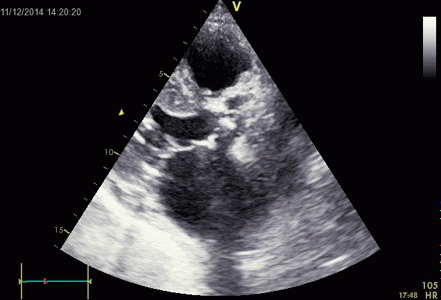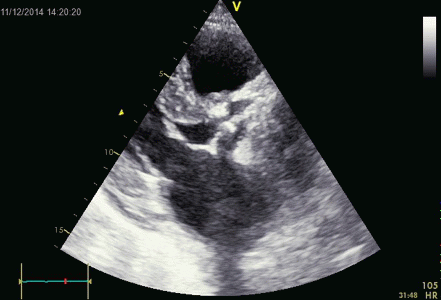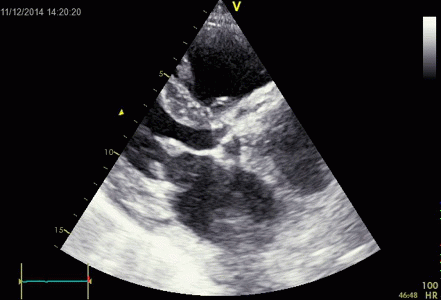
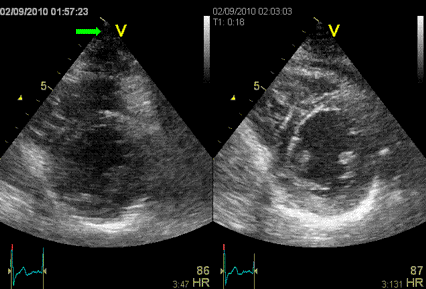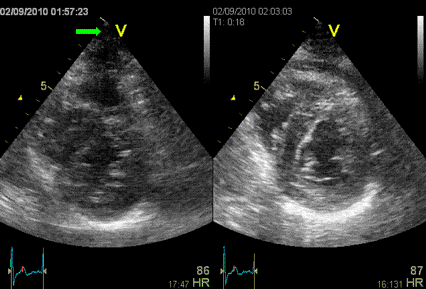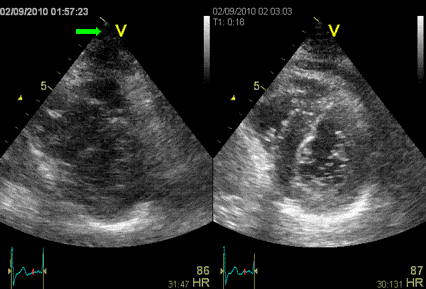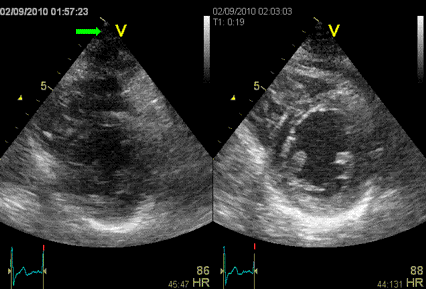
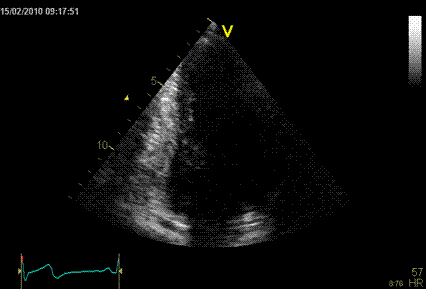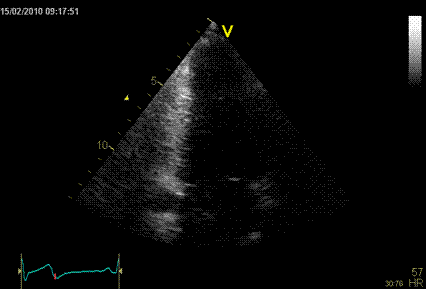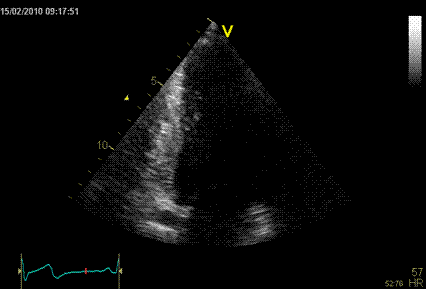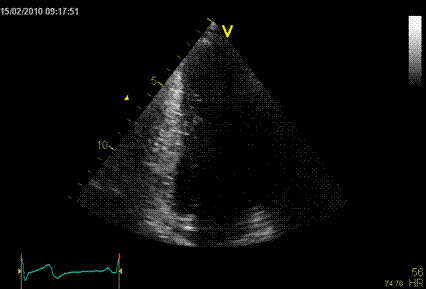
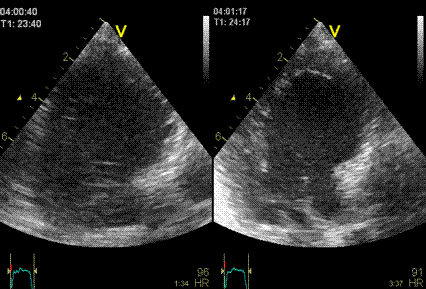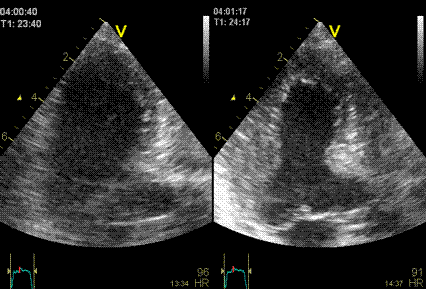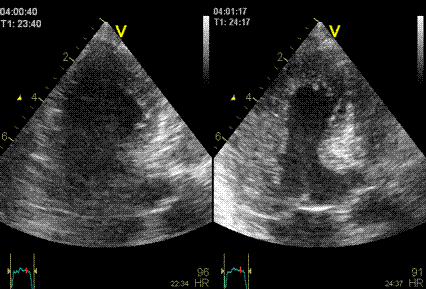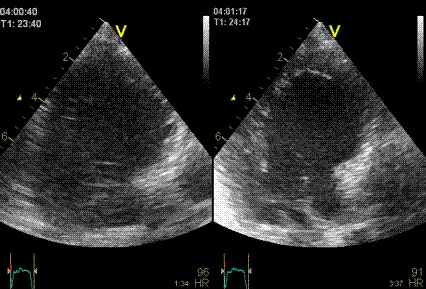
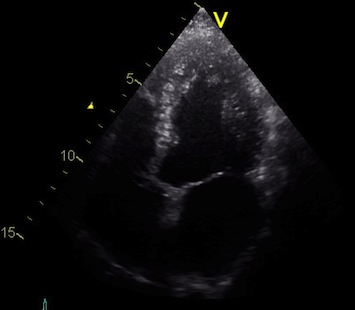
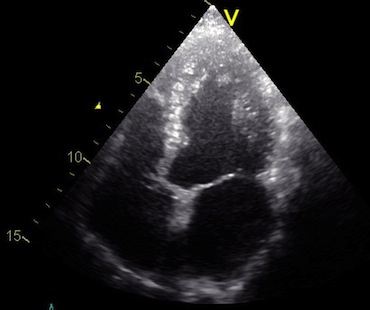
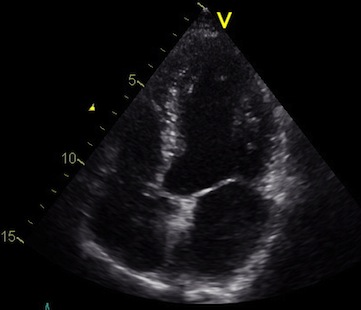
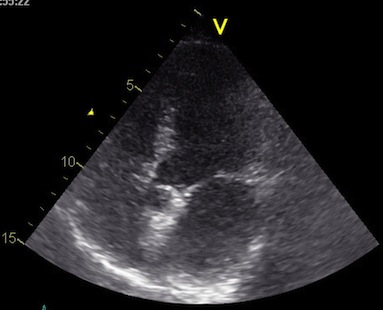
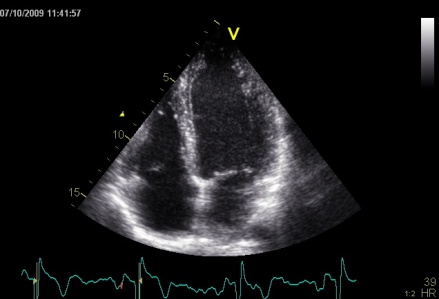
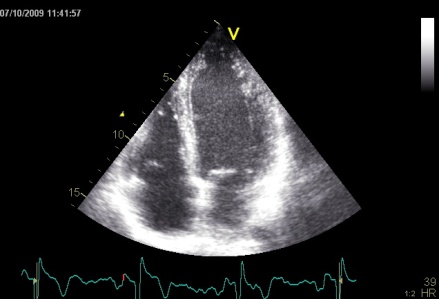
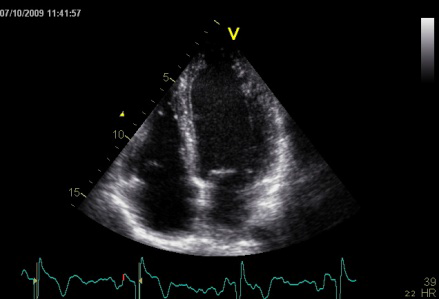
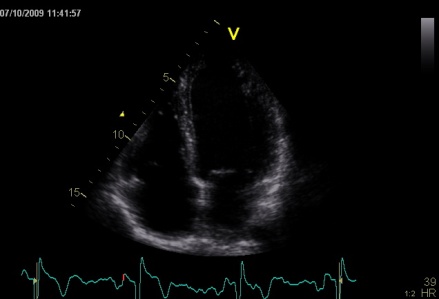
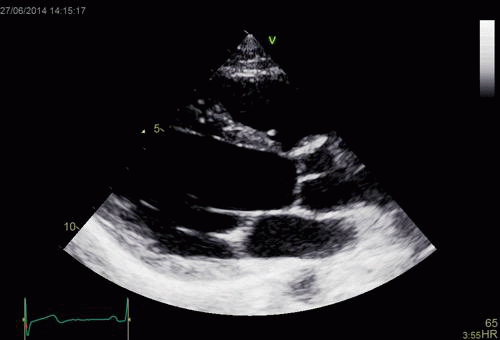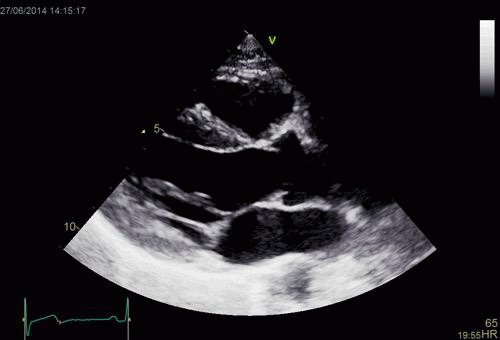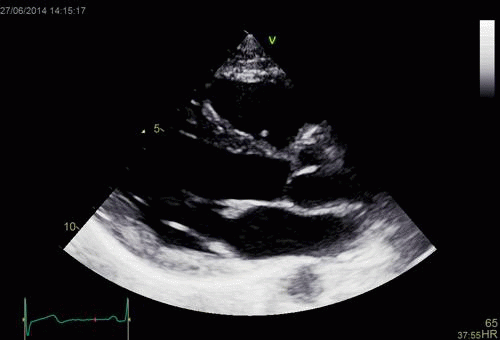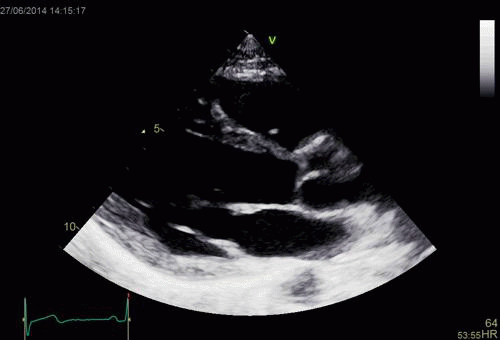
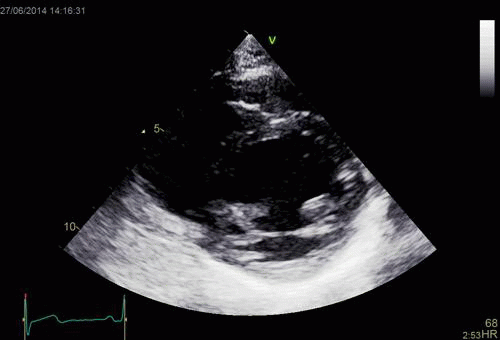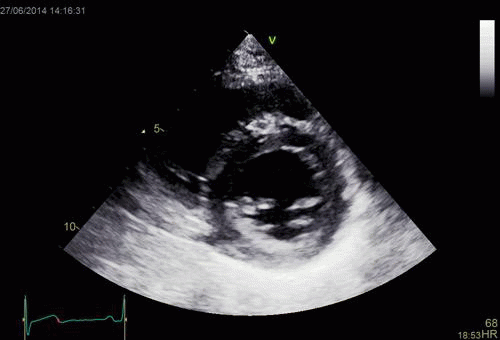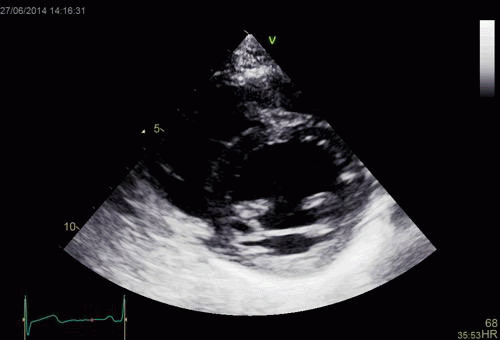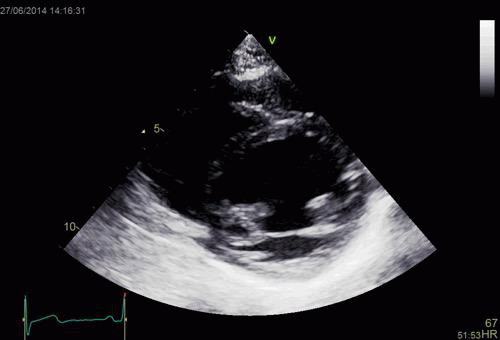
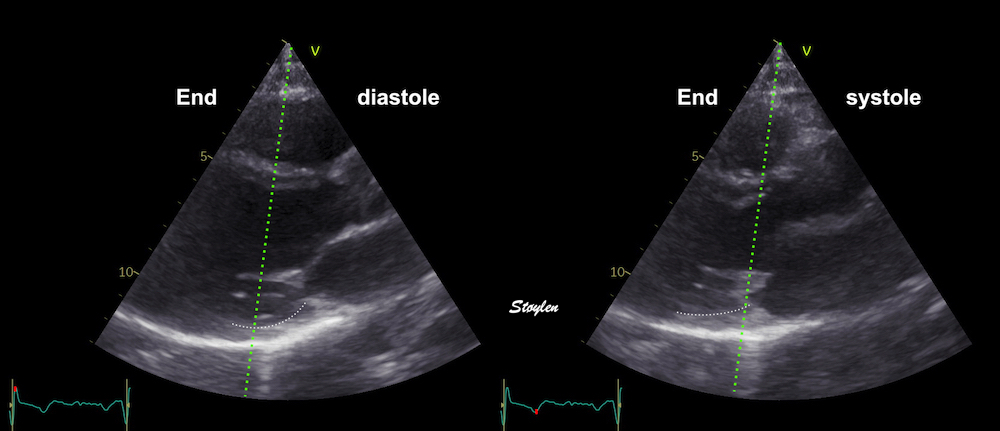
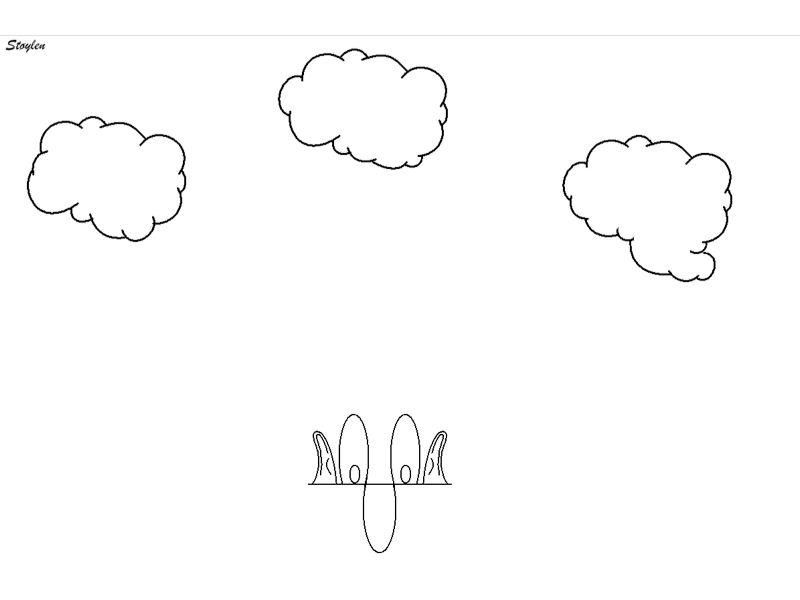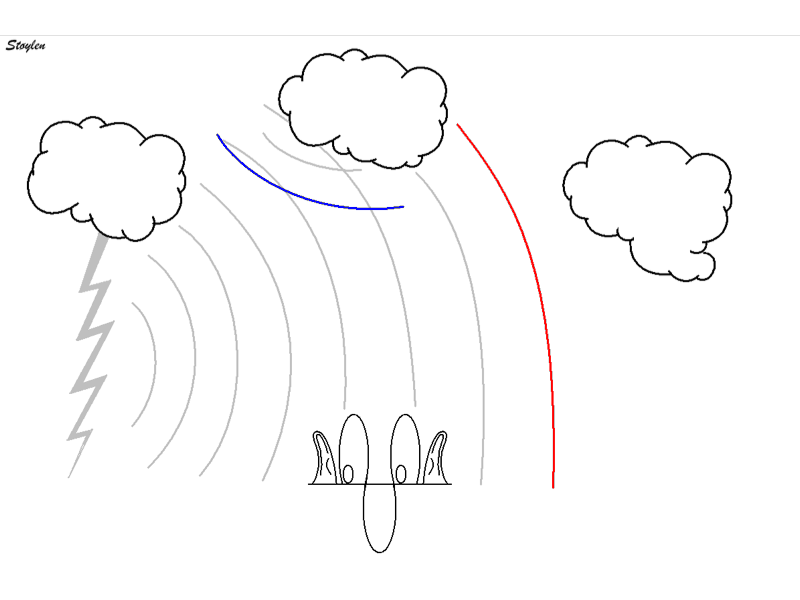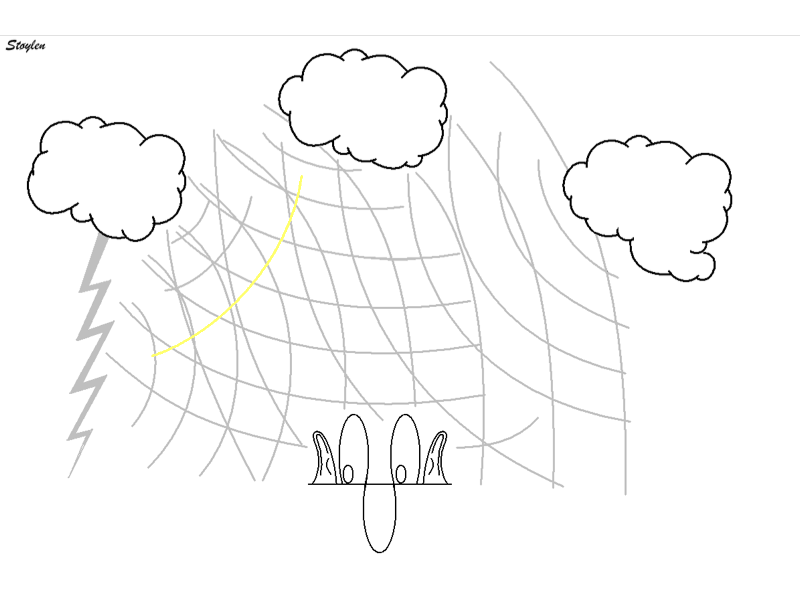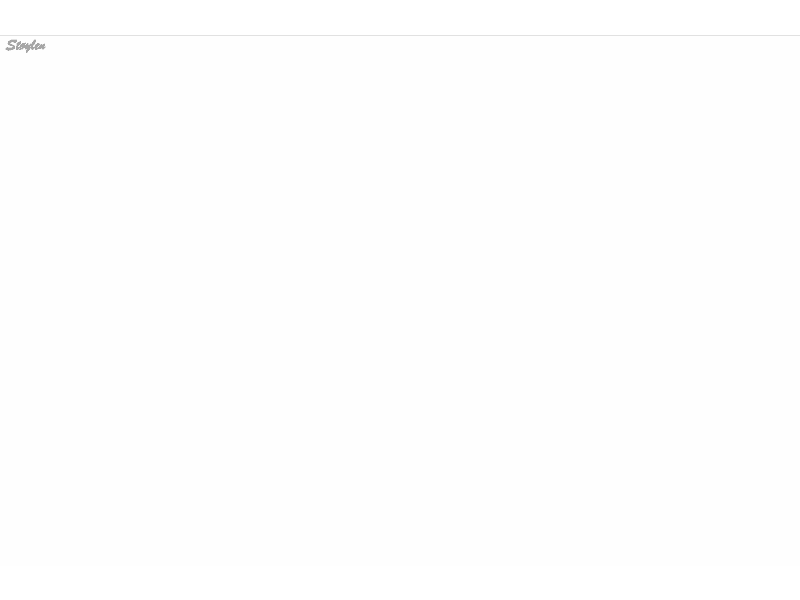
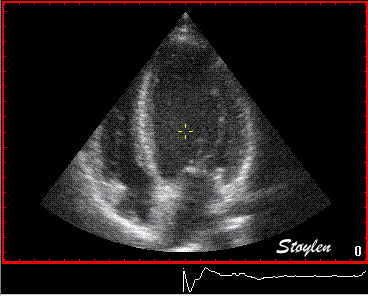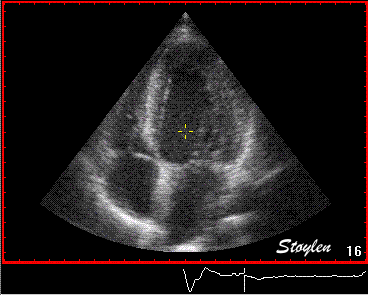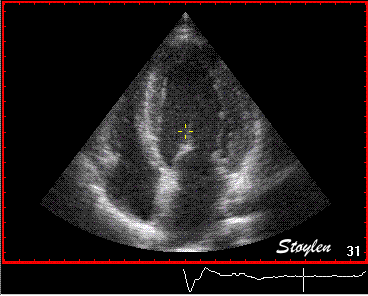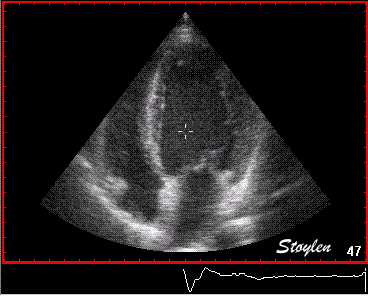
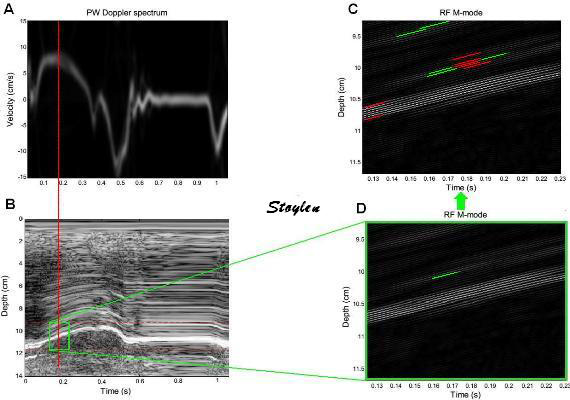
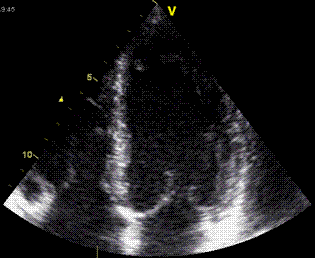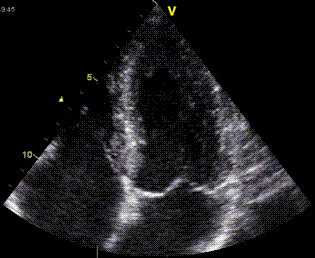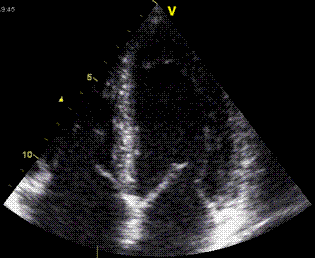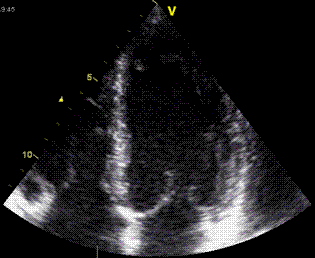
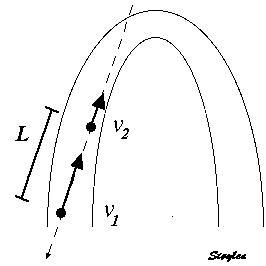
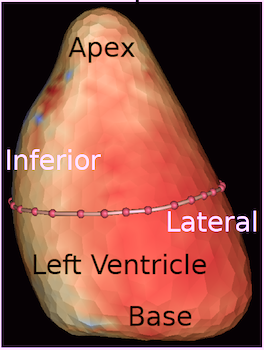
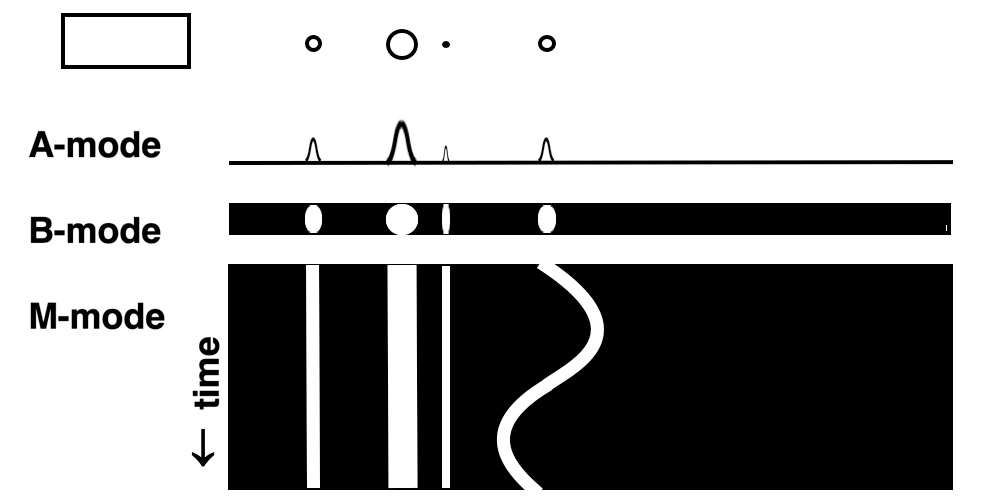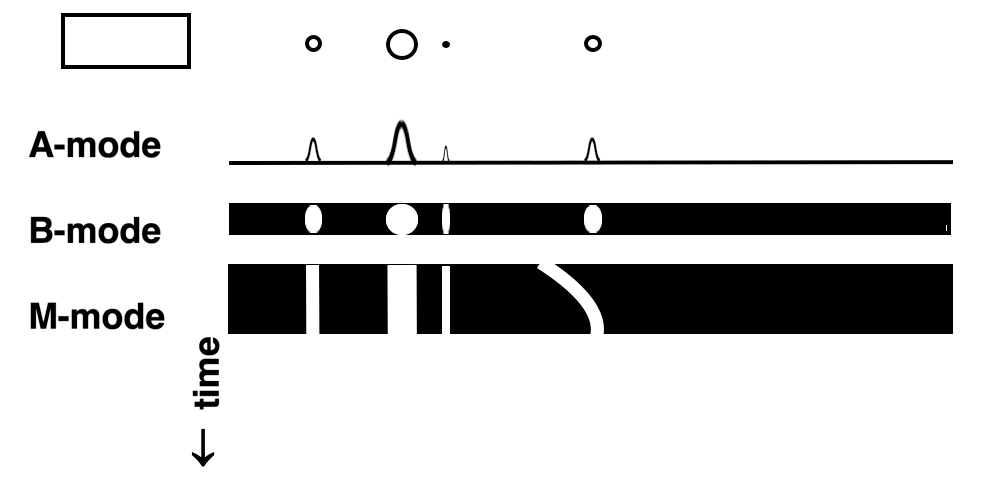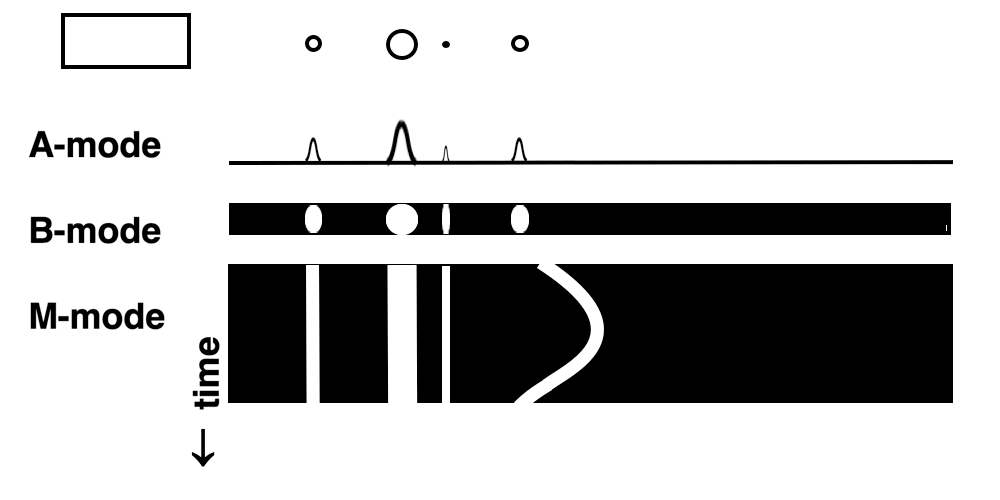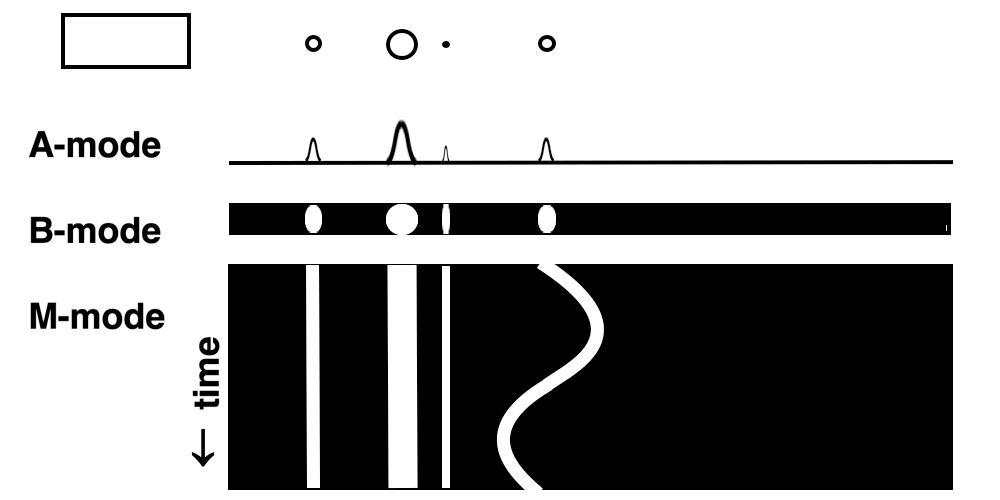
Images from different parts of the heart cycle, showing that the line crosses different parts of the LV in end diastole and end systole. As the end systolic frame has moved the base of the heart further towards the apex, and the posterior wall thickens towards the mitral annulus, the motion induces an apperent over estimation of end systolic thickness, which will be reflected in the M-mode measurements:

The apparent higher thickening of the posterior LV, may thus be due to the increased thickness of the posterior wall moving into the M-mode line due to the longitudinal motion of the basal parts of the heart.

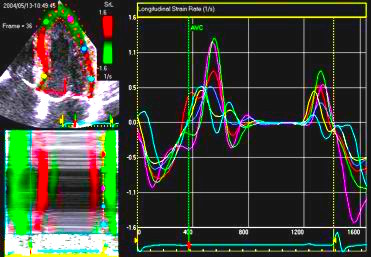
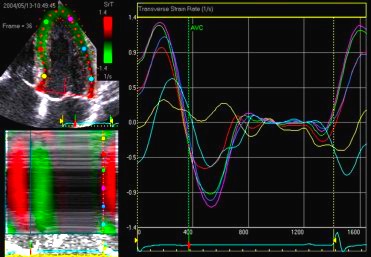
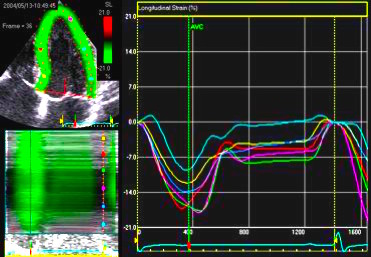
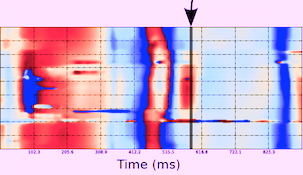
Comparing with longitudinal deformation of the two walls, we found in HUNT3 that MAPSE was about 14% higher in the posterior wall than the anteroseptum, but the posterior wall was also around 10% longer than the anteroseptum (156). Thus, the relative shortening (longitudinal wall strain) in HUNT 3 was 16.6% in the anteroseptum, vs 16.5% by segmental strain, and 14.7% vs 15.5% (relative difference 5%) by normalised MAPSE.

Thus, as longitudinal shortening and transverse thickening are interrelated as shown above, similar relative longitudinal shortenings between the walls, also indicates similar wall thickenings. Thus, the physiology weighs in favor of HUNT4 in this case, while the longitudinal and transmural deformation data in HUNT3 are somewhat inconsistent.

Beamforming

Again, modern technology now allows a much more complex processing technology allows using input data in a way that also improves the beamforming characteristics in processing, as they are used for the generation of a picture. Thus the simple principles of beamforming outlined here are an over simplification compared to the most advanced high end scanners.

It is important to realise that the last couple of years has seen tremendous improvements in both hardware (allowing a much higher data input to the scanner as well as processing technology), and software (allowing more data processing at higher speed). It even allow using input data in a way that also improves the beamforming characteristics in processing, as they are used for the generation of a picture. Thus the simple principles of beamforming and focussing outlined here are an over simplification compared to the most advanced high end scanners.

However, they will still serve to give an idea. And simpler equipment still conform more closely to the basic principles described here.

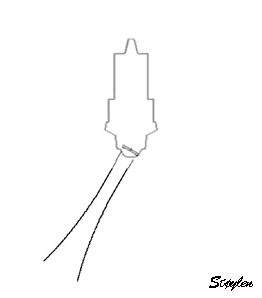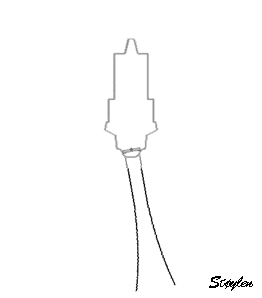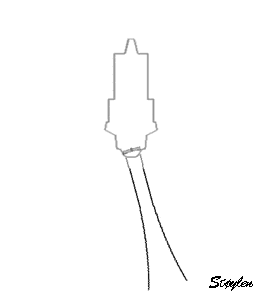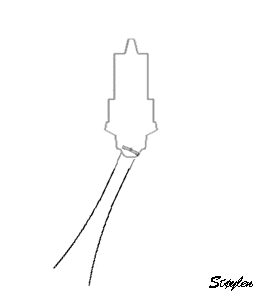
A. Mechanical transducer. The sector is formed by rotating a single transducer or array of transducers mechanically, firing one pulse in each direction and then waiting for the return pulse before rotating the transducer one step. In this beam there is electronic focusing as well, by an annular array.

B. Electronic transducer in a phased array. By stimulating the transducers in a rapid sequence , the ultrasound will be sent out in an interference pattern. According to Huygens principle, the wavefront will behave as a single beam, thus the beam is formed by all transducers in the array, and the direction is determined by the time sequence of the pulses sent to the array. Thus, the beam can be electronically steeredand will then sweep stepwise over the sector in the same way as the mechanical transducer in A, sending a beam in one direction at a time.

Beam focusing:


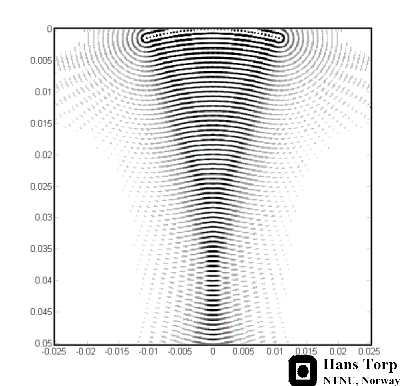
Dynamic focusing. The same principle of phase steering can be applied to make a concave wavefront, resulting in focusing of the beam with its narrowest part a distance from the probe. Combining the steering in B and C will result in a focussed beam that sweeps across the sector, as in the moving image above.	Resulting Ultrasound beam as shown by a computer simulation, focusing due to the concave wavefront created by the dynamic focusing. The wavelength is exaggerated for illustration purposes. Image Courtesy of Hans Torp.

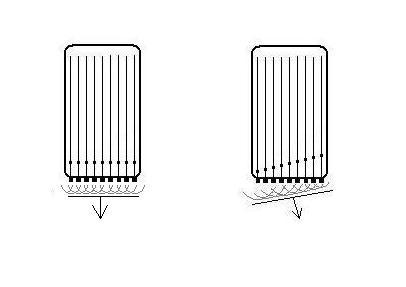
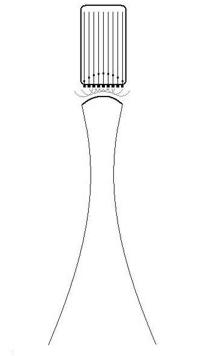
Focusing is illustrated above. In a mechanical probe, there may be several transducers, arranged in a circular array, focusing the beam in a manner analogous to that shown in fig. 7c. In a circular array, however, the focusing can be done in all directions transverse to the beam direction, i.e. in the imaging plane and transverse to the plane, while a linear array can only focus in one direction, in the imaging plane.

Annular focusing in all directions both in plane and transverse to the plane.

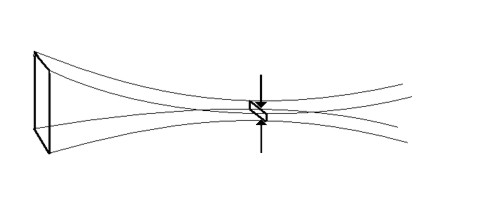
Linear focusing in the imaging plane only.

A matrix array, can focus in both directions at the same plane.

The focusing increases the concentration of the energy at the depths where the beam is focussed, so the energy in each part of the tissue has to be calculated according to both wavelength, transmission and focusing to ensure that the absorbed energy stays within safe limits.

Modern high end scanners has beams that are more focussed along the whole length, allowing narrower and more lines in the image, i.e. higher line density, and at the same time allows higher frame rate due to among other things MLA related image forming.

Unfocussed (planar) beams

In order to increase aperture size, the beams should be less focussed. In completely unfocussed beams, the wavefront is more or less flat, and the beam has more or less parallel edges.

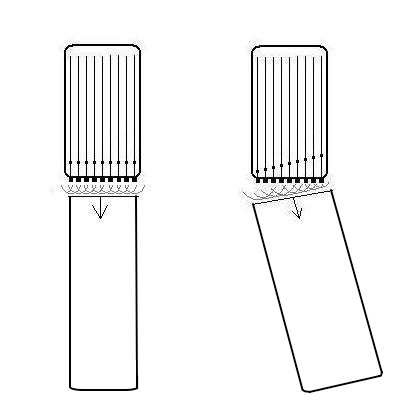
The advantage of this is:

Transmit beams can be broad, but still have a good resolution for multiple parallel receive beams (MLA). This will increase frame rate, as there can be only one broad transmit beam, instead of multiple scan lines. The high frame rate allows multiple measures within a short time frame.
MLA will not result in angle artefacts
Depth penetration is better, as the beams do not diverge by depth (below the focal point).

The main disadvantage is that with planar waves, the energy is too low for second harmonic imaging, Thus, it cannot be used for B-mode imaging, neither in 2D nor 3D. However, it can be used for tissue Doppler, where harmonic imaging is unfeasible anyway, because of the Nykvist limit.

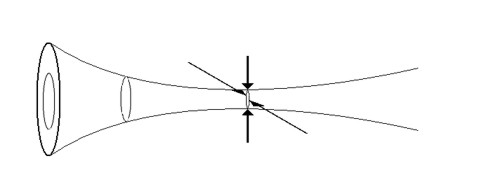
Lateral resolution

The apparent width of the scatterer in the image is more or less given by the lateral resolution of the beam. (The thickness in the axial direction is determined by the depth resolution, i.e. the pulse length as discussed above). In addition, two echoes within one beam, will only be separated by the difference in depth.


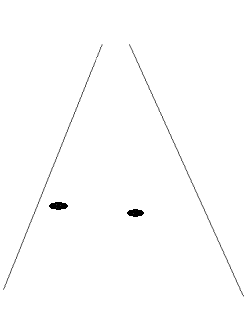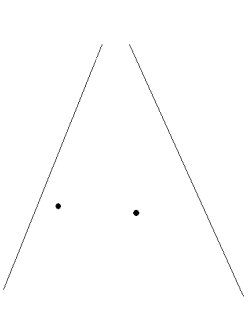
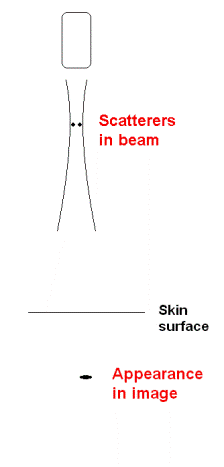
The lateral resolution of a beam is dependent on the focal depth, the wavelength and probe diameter (aperture) of the ultrasound probe. A near shadow will reduce the effective aperture, and thus the lateral resilution as illustrated here. (Reproduced from Hans Torp by permission)	Two points in a sector that is to be scanned.	The ultrasound scan will smear the points out according to the lateral resolution in each beam.


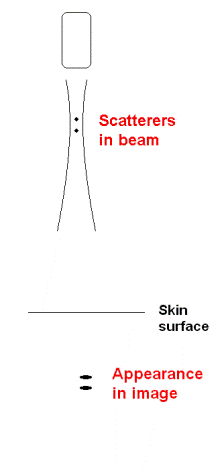
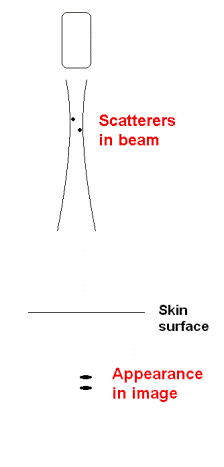
Thus a small scatterer will appear to be "smeared out", and the apparent size in the image is determined by the beam width and pulse length. As the pulse length is less than the beam width, the object will be "smeared out" most in the lateral direction.	Two scatterers at the same depth, separated laterally by less than the beam width, will appear as one.	Two scatterers at different depths will appear separate if separated by more than the pulse length.	But, if separated both laterally and in depth, they will appear as being in the same line, if lateral separation is within the beam.

Artefacts

Reverberations:

Reverberations is defined as the sound remaing in a particular space after the original sound pulse has passed.
Thus, a single echo is a reverberation (first order), and multiple echoes will be higher order reverberations as illustrated below.

the phenomenon that a sound pulse bounce back between different structures before being reflected back to the observer. , while in ultrasound iomages the term is usually restricted to artefacts caused by the echo bouncing more times (higher order reverberations) , creating false images

The phenomenon of thunder is a typical reverberation effect:

Reverberations: Simplified animation of thunder. The sound of lightning is a short, sharp crack. The wavefront of that sound (red) reaches the listener first, but the wavefront is then reflected from different cloud surfaces with different distance to the listener as secondary echoes, ( primary reverberations; blue and green), an also tertiary echo (Secondary reverberation; yellow) and even higher orders. Thus, the crack is "smeared out" to a long lasting rumble.

In ultrasound imaging, actually the primary echoes are first order reverberations. However, in ultrasound images the term is usually restricted to artefacts caused by the echo bouncing more times (higher order reverberations) , creating false images as the partial delay due to multiple reflections will be interpreted as images at greater and different depths. One of the most typical phenomenons are the stationary reverberations caused by the bouncing of the pulse between a structure close to the surface, and the probe surface:

Stationary reverberations are caused by stationary structures, usually in the chest wall, causing the ultrasound to bounce back and forth between the skin and the structure, increasing the time before the echo returns and giving rise to a false image of an apparent stationary structure deeper down.



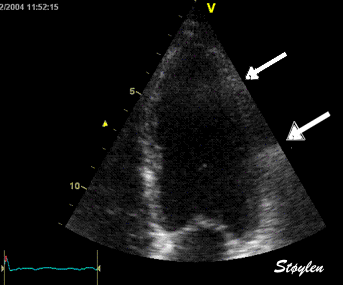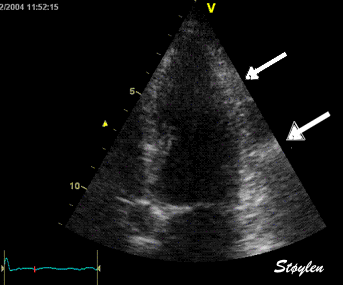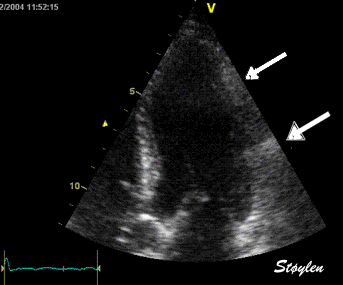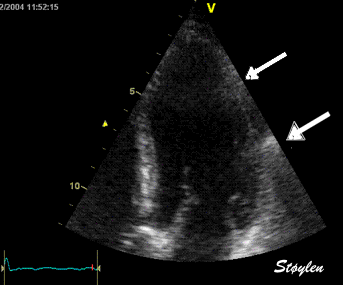
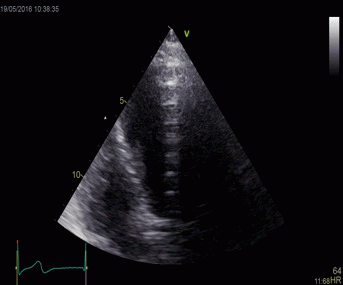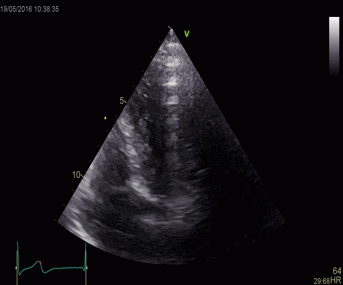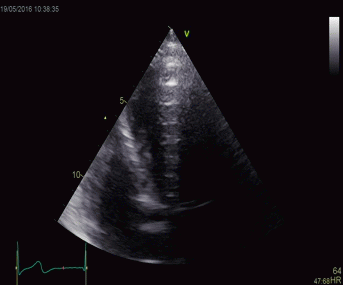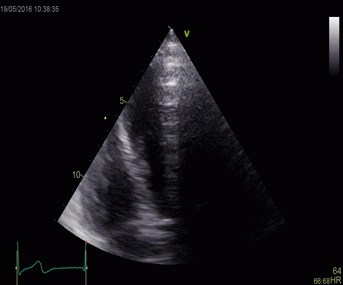
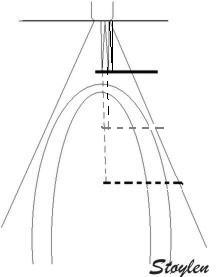
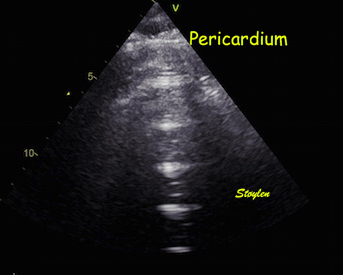
Top, a common reverberation in the lateral wall, seen as a stationary echo (arrows). Below, the principle shown diagrammatically, a reflector causing the ultrasound pulse to bounce, for each bounce back, the echo is interpreted as a structure at a depth corresponding to multiples of the original depth.	This is even more evident in this image, showing multiple, stationary reverberations from the apex. All the reverberations have the same distance. In the blow up below, the reverberation space can be seen to be a echolucent space in front of the apical pericardium, and the distance between the reverberations equals the original distance between the probe and the pericardium.

Reverberations needs not necessarily be totally stationary, if the reflecting surface that gives rise to the echo moves, the reverberations will move as well.

Reverberations in colour Doppler

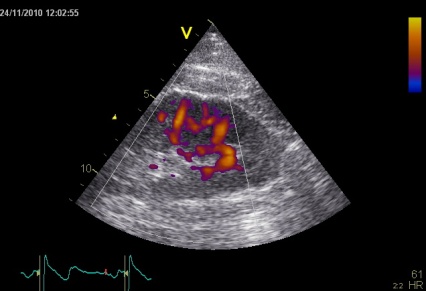
Reverberations may also occur in colour Doppler:


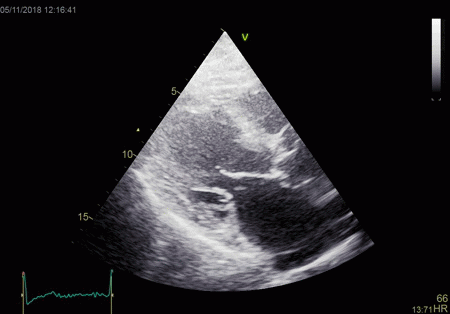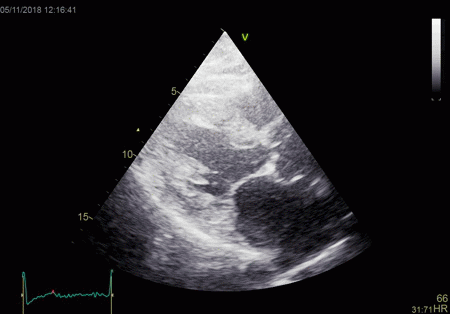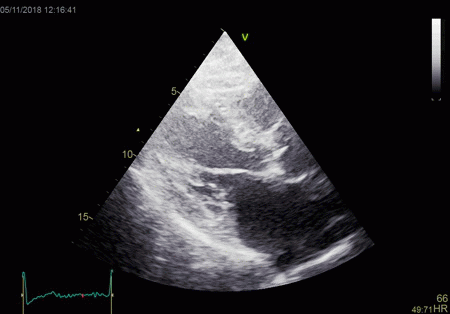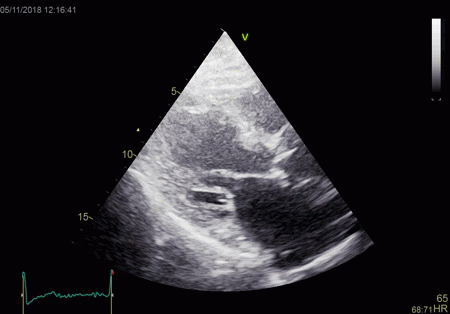
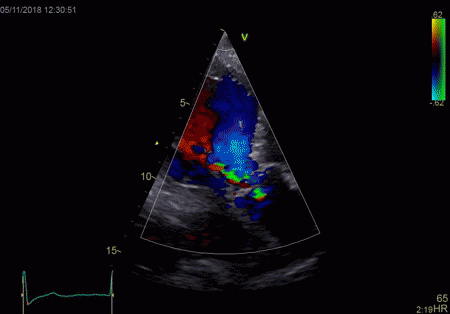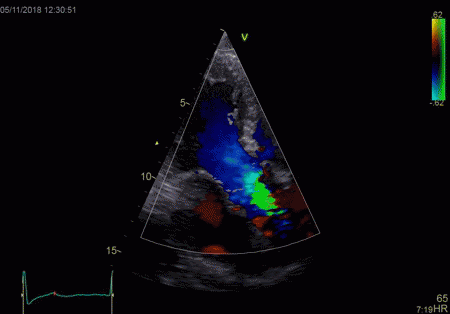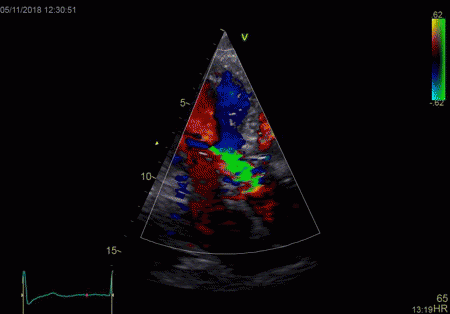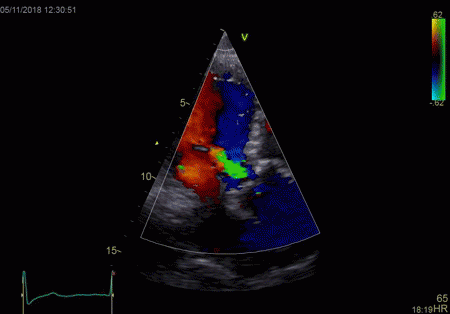
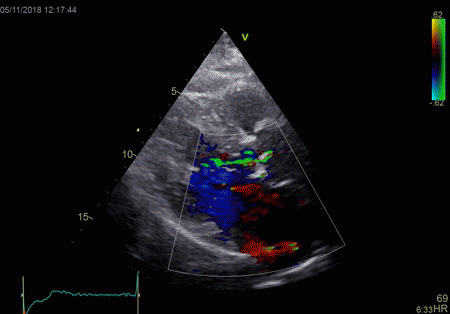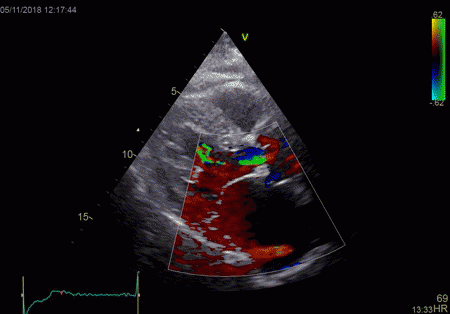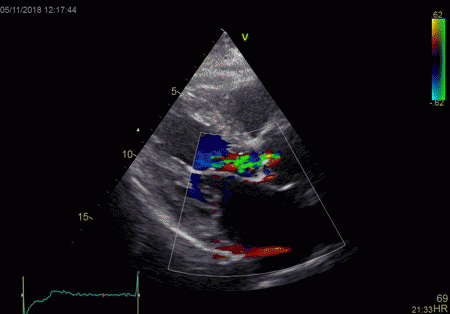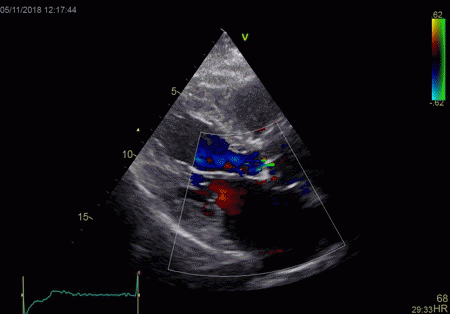
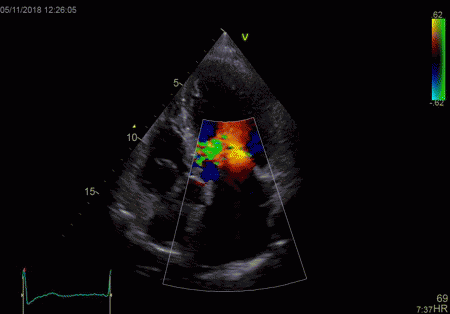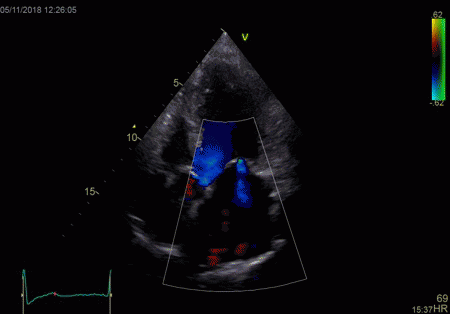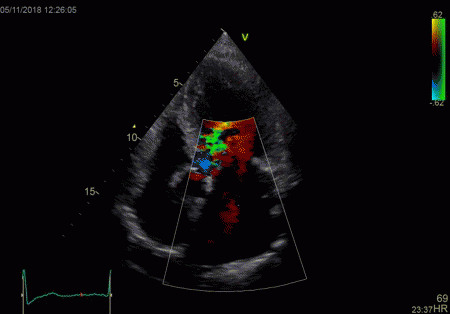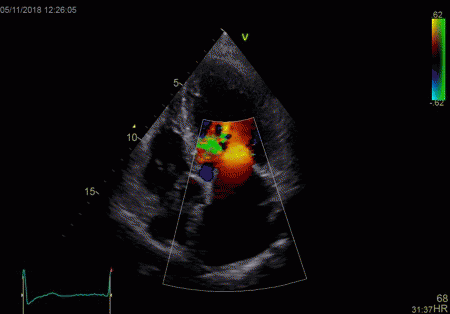
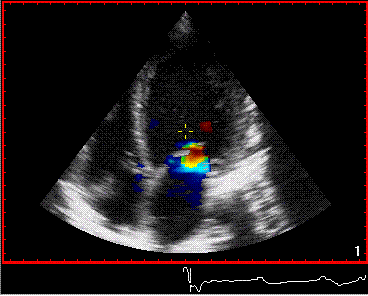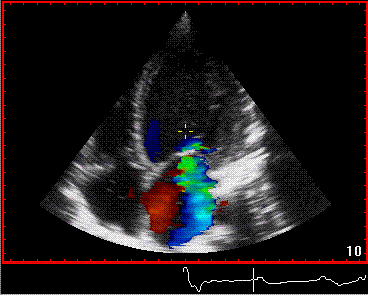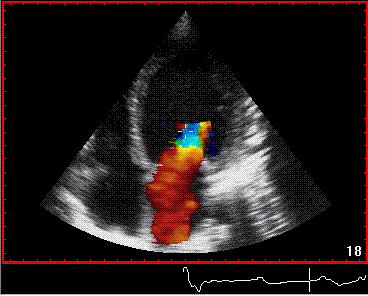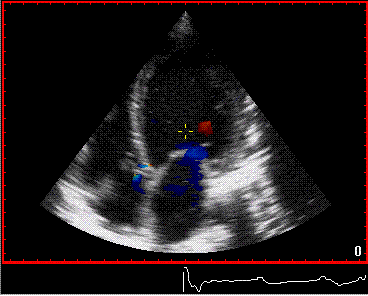
The red jet shown in the atrium, is a reverberation originating from the aortic regurgitation jet.	From the B-mode acquisition, there can be seen a slight, possibly clutter line as well, buty in this case the reverberation signal is predominantly in the Doppler signal.

To document that this is not a pathological jet, the apical long axis and four-chamber views do not show such a jet in the same location.


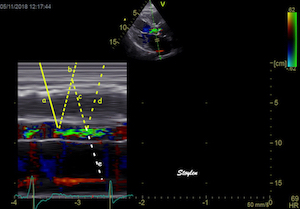
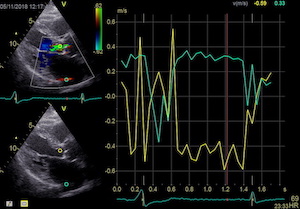
The simultaneous duration of the two jets shown on the reconstructed M-mode also confirms that this is a reflection, and not something else (f.i. a venous signal or fistula)	The distance between the jets is compatible with the reflecting layer being the immovable structure outside the pericardium.	-and quantitative analysis shows the reversal of the phase in the reflected signal.

Ring down artefacts

The "ring down" phenomenon is a special instance of reverberations in the form of a bright beam radiating out behind a small echo lucent (often fluid filled, but may be fat) layer behind a scatterer with high reflexivity. The source of the ring down artefact is thus a small reverberating space in front of a powerful reflector, despite the fact that it is projected behind it.

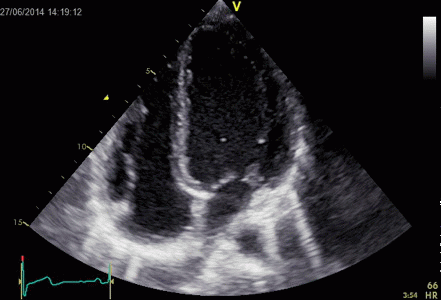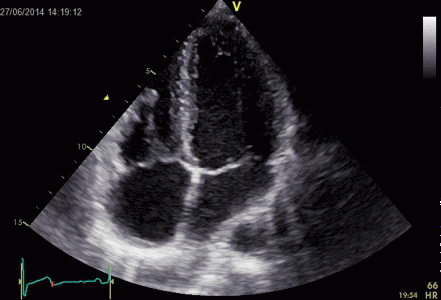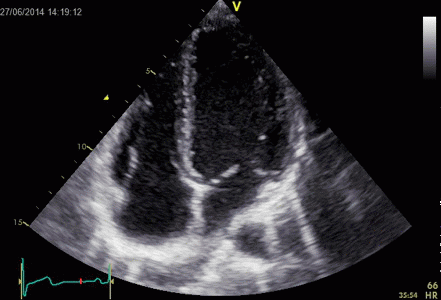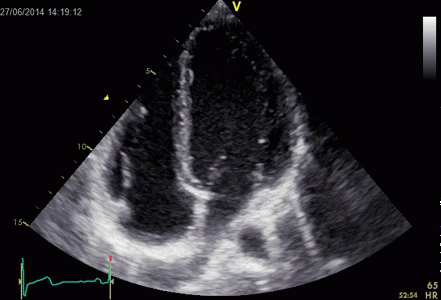Ringdown artefacts in an echo from a healthy (and young) person originating from the base of the left ventricle and right atrium. As explained below, they most probably originate from the pericardial space. The persistence of the phenomenon through the depth may partly be a function of the Time Gain Compensation, and the fan like appearance of course, is due to using a sector scanner.

This artefact was originally described in relation to small gas bubbles in the abdomen, and also to small cholesterol crystals in the gall bladder. However, as seen above and below, small structures in the pericardium as well as mechanical valve components, may also give rise to this. The mechanism has been proposed as being resonance, i.e. that the pulse hitting a small gas bubble or cluster of bubbles may give rise to the bubbles resonating, and thus emitting energy long after the original pulse has been reflected. In the scanner this would be interpreted to successive echoes in the same direction, but with increasing depth, i.e. a bright ray. In echocardiography, however, it is not uncommon, most often from the pericardium. Normal subjects, of course, do not have air in the pericardium.

If present, they do not disappear with change of probe frequency, excluding resonance as a mechanism:

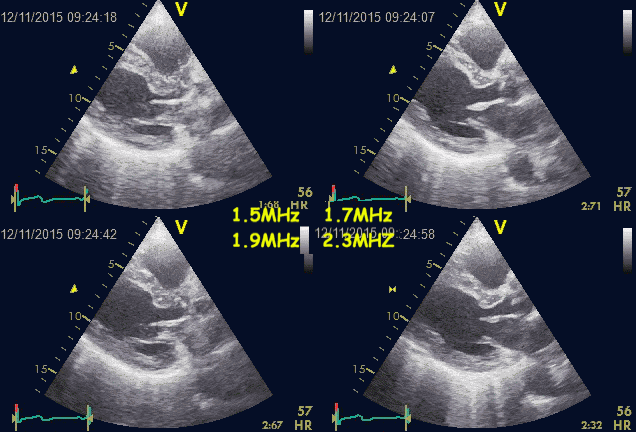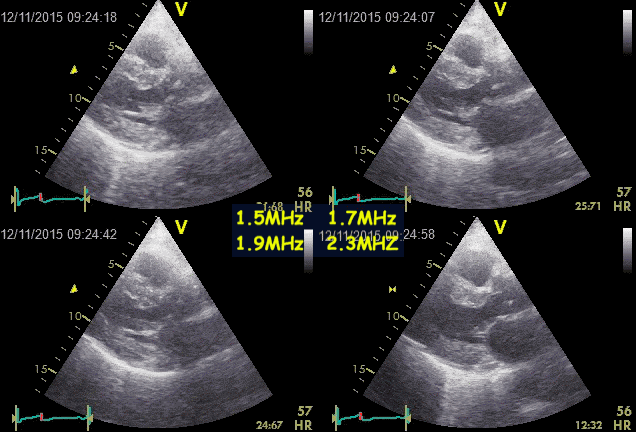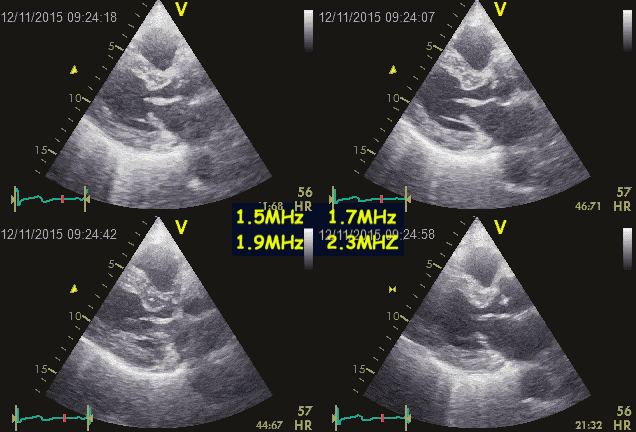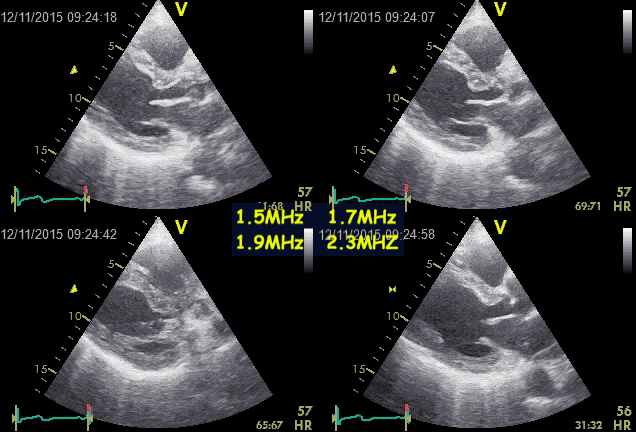Ringdown artefacts from the pericardium. As seen by this image, they are present with all probe transmission frequencies, which would not be the case if this was due to resonance.

Resonance is basically related to a specific frequency, the eigenfrequency of the source. Frequencies above that can basically cause resonance, but mainly in the harmonic frequencies, i.e. those that are one or more octaves (multiples of the basic frequency) removed from the eigenfrequency. In the example above, the artefact is present with frequencies that are not multiples of each other, so resonance is ruled out.

Thus, the ring down artefact is a special instance of reverberations, where there are multiple reverberations within a short space as illustrated in the diagram below:

Reverberations. In all cases, reverberations are the result of the ultrasound pulse bouncing back and forth between two layers, the low reflecting space between them can be called the "reverberation space". Here the probe surface is shown in black, the reflector causing the reverberation in dark grey, while the artefact echoes are shown in lighter grey. The reverberation space in front of the reflector is illustrated in light red.

A: Classical reverberation where the echo bounces between a reflector at some depth, and the probe. This gives rise to the classical reverberation, showing up as one or two stationary shadows, as shown above.
B: With a shorter reverberation distance, the distance between the reverberations (artefact shadows) decreases, and more false echoes with the same distance between them arises, lying on a line.
C: With a very short reverberation distance, the reverberation echoes lies so close as to give the impression of a beam.
D: the reverberation space may be due to a minimal layer of low reflecticvity (for instance a minimal layer of pericardial fluid or fat) in front of a dense structure (the parietal pericardium)at some depth from the probe. In that case, the beam will seem to originate here, and not close to the probe.

It is clear that fluid filled layers in the body may act as reverberation spaces, provided the structure behind is sufficiently reflective. In the lungs, this phenomenon is seen in connection with oedema in the interlobular septa. The air space in the alveoli is almost totally reflective. This is called comet tails.

Comet tails

The comet-tail artefact is used to describe the ring down phenomenon doing utlrasound of the lungs, with a cardiac probe (281). This has been seen to be a marker of interstitial fluid in the lungs (282), i.e. edematous interstitial septa (equivalent to the Kerley B-lines on X-ray), and has been seen to be quick and reliable. The reverberations should then be within the edematous interstitial septa, as air filled alveolar clusters in front and behind would be strong reflectors, causing the reverberation within a very short distance (283). As penetration through the lung is poor, they have to originate close to the lung surface:

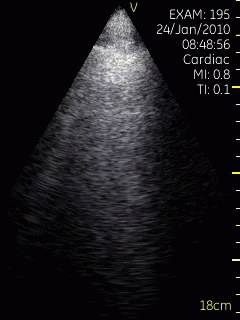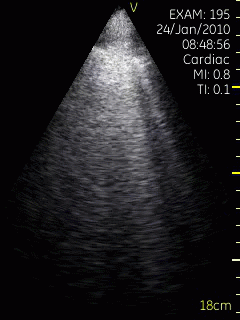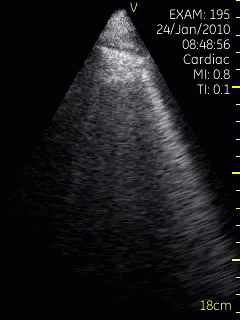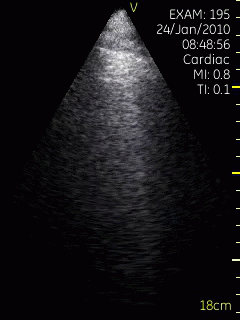Lung ultrasoud showing comet tails from a patient with heart failure. In this case theymove with the lung during rspiration. The lung tissue can be seen in the upper few centimeters, below that the signal is totally attenuated, but the comet tails are clearly visible. Image acquired with a hand held ultrasound device. Image courtesy of Bjørn Olav Haugen, NTNU

As with calcification shadows, it is an example of an artefact giving useful information.

The source of the ring down artefact is a small reverberating space in front of a powerful reflector, which means that the reflector may give rise to an attenuation shadow as well. This is also shown up in the cone behind the reflector, and this attenuation shadow itself may act to increase the apparent gain of the ringdown beam.


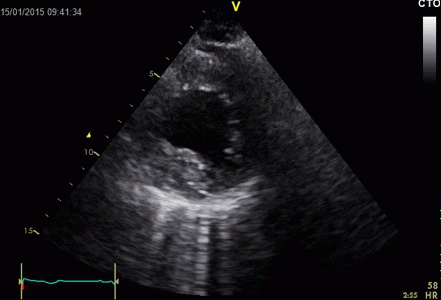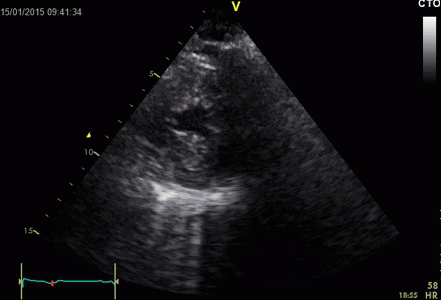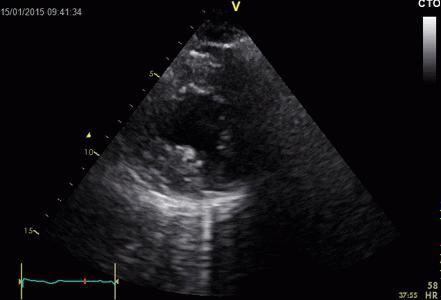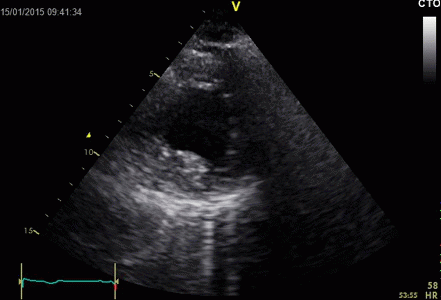
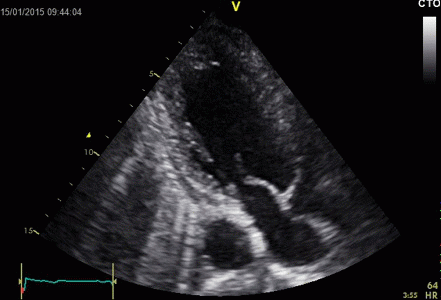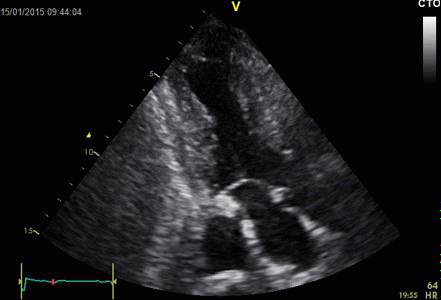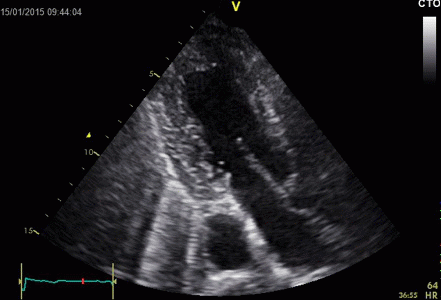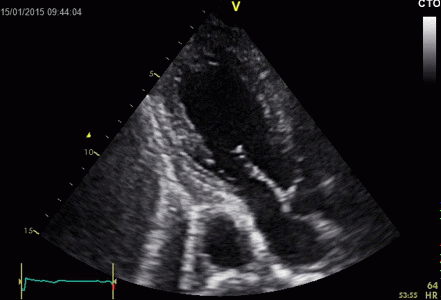
Ring down echoes from the pericardium. They can be seen as bright bands radiating down, and the source seem to be real, as the ring down beams are visible both in long and short axis views from the same patient. The reverberating space is probably the pericardial space itself. The uneven distribution of the ring down beams may be due to the varying reflectivity due to different directions of the surfaces relative to the transmitted beams.

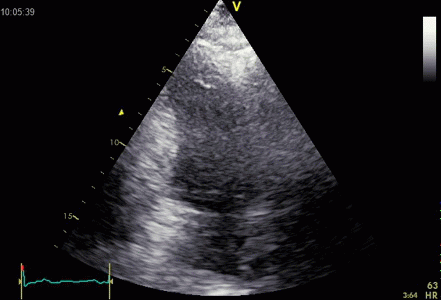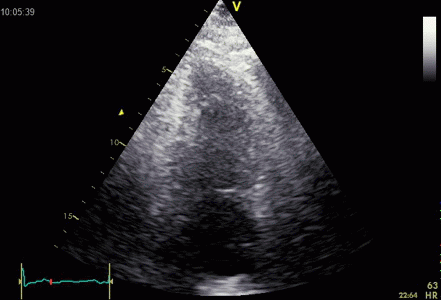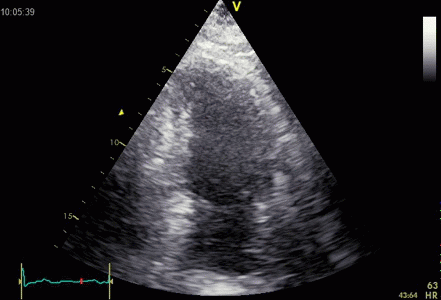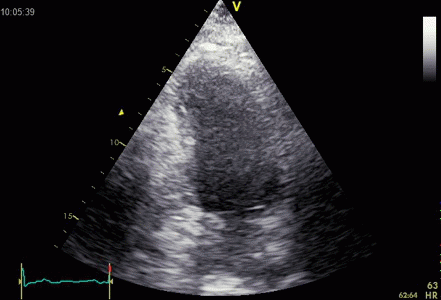
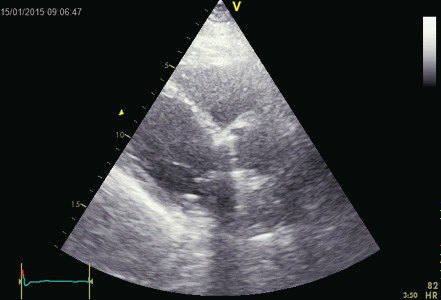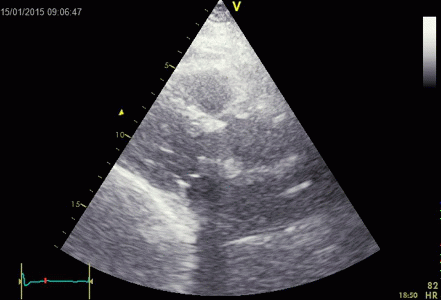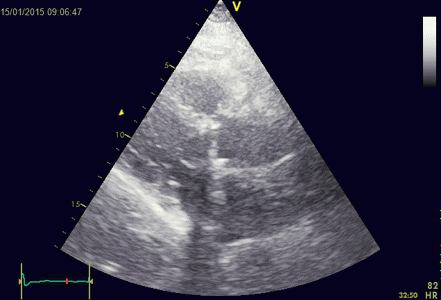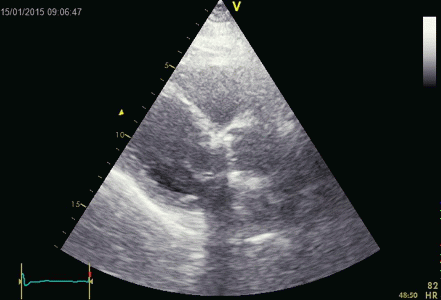
Ring down beam seen to originate from the apicolateral pericardium. As with sidelobes, in this case the shadow is not constant, probably due to the source moving in and out of the plane.	Parasternal image from a patient with a mechanic aortic valve, combining shadows and ring down shadows. The thick metal ring itself gives rise to an ordinary shadow from the anterior part,, while the thin part of the carbon fibre ring protruding out into the sinus valsalvae, gives rise to a ring down beam. The reverberating space may be the sinus in front of the protruding carbon ring.

Discrete reverberations as shown above, is due to the fact that the signal remains coherent, i.e. remains reciognisable by the sacnner as a distinct echo.

Also, the echoes may be scattered in all directions, the pulse may bounce in different directions (as in the thunder animation above) before part of the reflected pulse reaches the probe. Also The refelcted signal looses it's coherence. This will not give a distinct echo like the one above, but rather more diffuse, less dense shadows, as in the example below:


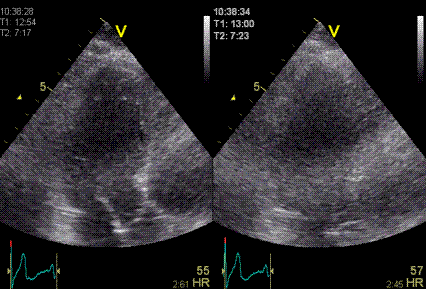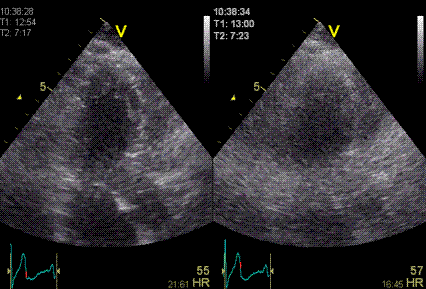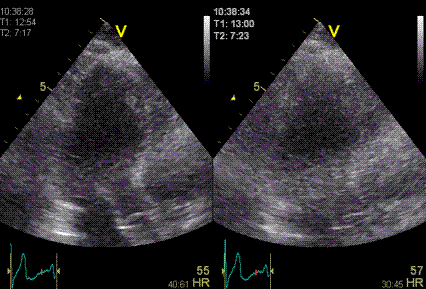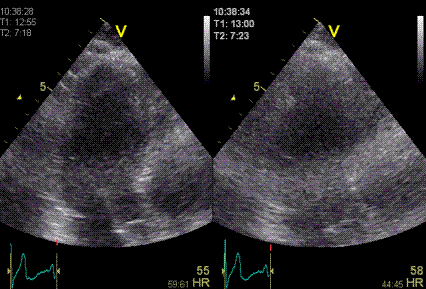
Heavy reverberation band across this long axis image. The shadow is not ditinct, and thus far less coherent than the examples above.	Shadowy reverberations covering the naterior wall in this 2-chamber image. It is differentiated from the drop out shown above, as we can se a "fog" of structures covering the anterior wall. The structures are stationary. On the other hand, this is not distinct reverberations shadows, but incoherent clutter.

Shadowy reverberations may seem of little importance, as the B-mode often is faily well visualised anyway. This is partluy due to the motion, and partly due to the second harmonic mode, which reduces the amplitude of reverberation noise, but only in the B-mode, as tissue Doppler must be done in fundamental mode due to the Nykvist limit.

The impact of reverberations on tissue Doppler are discussed below, on strain rate imaging by tissue Doppler in the measurements section, and on speckle trackingin the measurements section here and here.

Stationary echoes and noise is also referred to as "clutter". This noise may also result in a more random pattern (shadowy reverberations), resulting in a more blurred picture.

Side Lobes

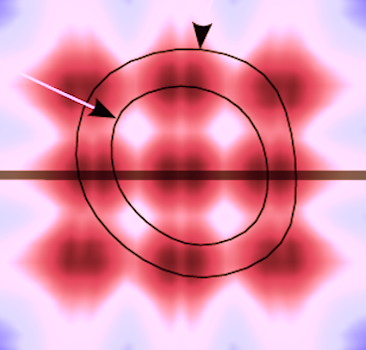
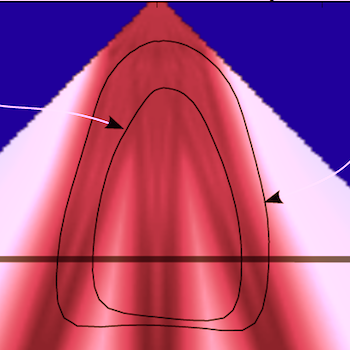
Each beam is not solely concentrated in the main beam as illustrated above. In addition, some of the energy is dispersed in side lobes originating among other things from interference as illustrated below.


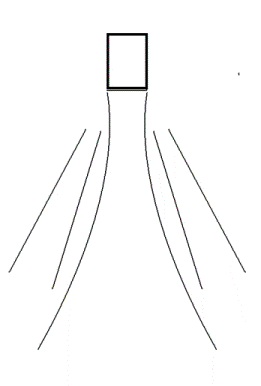
Simulated beam with focusing, showing interference pattern dispersing some of the beam to the sides. (image courtesy of Hans Torp).	Side lobes from a single focussed ultrasound beam. These side lobes will also generate echoes from a scatterer hit by the ultrasound energy in the side lobes, i.e. outside the main beam.


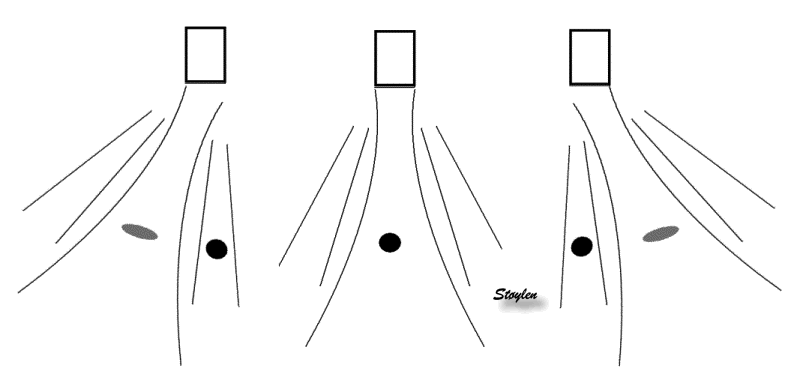
As echoes from a scatterer in the side lobe pathway is perceived coming from the main beam, this will result in a false echo, apparently from the main beam..	AS the beam with side lobes sweeps back and forth a cross the sector, each echo from the scatterer in both the main beam and the side lobes will generate the false echo in the position of the main beam.	This again will result in the echo being smeared out across the sector, resulting in a smeared out echo across a large part of the sector.

Patient with an aortic valve. The strong echo from the metal in the ring creates sidelobes across most of the sector. It can be seen to move awith the AV-plane motion as expected.

IN most cases, the sidelobes originate form less intense echoes, which gives smaller sidelobes, that are more difficult to discern from real structures.


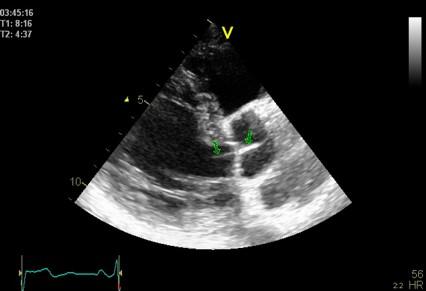
Side lobes originating from the fusion line of the aortic cusps, seen to extend into both the LV cavity and the aortic root cavity (arrows).	As opposed to reverberations, the side lobes moves with the structure, and may change with time (in this case the echo intensity of the fusion line decreases as the valve opens, and thus the intensity of the side lobes too) .

As opposed to reverberations, the side lobes will move as well as increase and decrease in intensity in parallel with the source of the echo as shown below.

2-dimensional imaging:

A 2-dimensional image is built up by firing a beam vertically, waiting for the return echoes, maintaining the information and then firing a new line from a neighboring transducer along a tambourine line in a sequence of B-mode lines. In a linear array of ultrasound crystals, the electronic phased array shoot parallel beams in sequence, creating a field that is as wide as the probe length (footprint). A curvilinear array has a curved surface, creating a field in the depth that is wider than the footprint of the probe, making it possible to create a smaller footprint for easier access through small windows. This will result in a wider field in depth, but at the cost of reduced lateral resolution as the scan lines diverge.


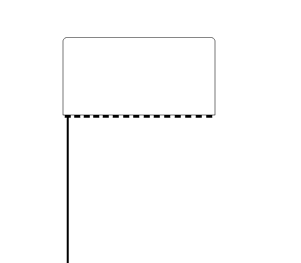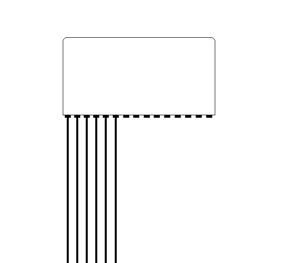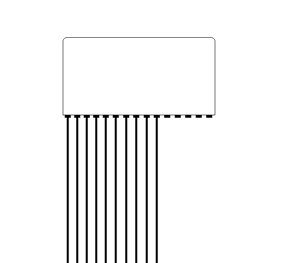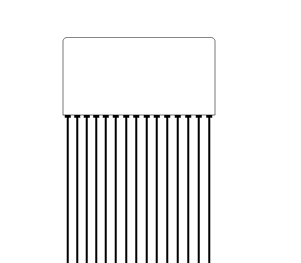A pulse is sent out, ultrasound is reflected, and the B-mode line is built up from the reflected signals.		Linear array.	Curvilinear array

The linear array gives a large probe surface (footprint) and near field, and a narrow sector. A curvilinear array will also give a large footprint and near field, but with a wide sector.

But in order to achieve a footprint sufficiently small to get access to the heart between the ribs, and with a sufficiently wide far field, the beams has to diverge from virtually the same point. This means that the image has to be generated by a single beam originating from the same point, being deflected in different angles to build a sector image (cf. figs. 6 and 7).

This can be achieved by a single transducer or array sending a single beam that is stepwise rotated, either mechanically or electronically.
A very small footprint can be achieved by a mechanical probe, sending only one beam, but being mechanically rotated by a motor. Finally with a slightly larger footprint, a phased array with electronic focusing and steering, can generate a beam sweeping at an angle similar to the mechanical probe. Beamforming by phased array, also enables focusing of the ultrasound beam as shown. Focusing can also be performed in a mechanical probe, by a concentric arrangement of several ring shaped transducers, an annular array. This will focus the beam in both transverse directions at the same time.

The next line in the image is then formed by a slight angular rotation , making the beam sweep across a sector:

The next line in the image is then formed by a slight angular rotation , making the beam sweep across a sector:


By making the ultrasound beam sweep over a sector, the image can be made to build up an image, consisting of multiple B-mode lines.	c. In principle, the image is built up line by line, by emitting the pulse, waiting for the reflected echoes before tilting the beam and emitting the next pulse. Resulting in an image being built up with a whole frame taking the time for emitting the total number of pulses corresponding to the total number of lines in the image.

This means that as a pulse is sent out, the transducer has to wait for the returning echoes, before a new pulse can be sent out, generating the next line in the image.

2D echocardiography. A line is sent out, and as all echoes along the beam are received, the picture along the beam is retained, and a new beam is sent out in the neighboring region. building up the next line in the image. one full sweep of the beam will then build up a complete image; i.e one frame. A cine-loop is then a sequence of frames; i.e. a movie.

The present technology is sufficient to build up a picture wit sufficient depth and resolution with about 50 frames per second (FPS), which gives a good temporal resolution for 2D visualisation of normal heart action ( about 70 beats per min.). However, the eye has a resolution of about 25 frames per second, so there may seem to be excess information. But off-line replay may be done at reduced frame rate, thus enabling the eye to utilise a higher temporal resolution.

Line density

The width of the echo will be determined by the beam width, and thus the distance between the beams (most ultrasound scanners today will intrapolate between beams if the distance between the beams is greater than the beam width). Ideally, the distance between the beam width should be the same as the beam width at the focal depth, for maximal resolution, thus lateral resolution of a beam determining the line density. This means that the line density would be suited to the beam width. This, however, holds only for a linear array.

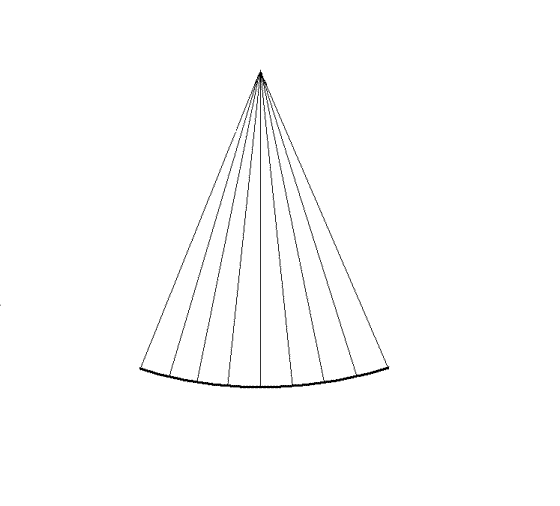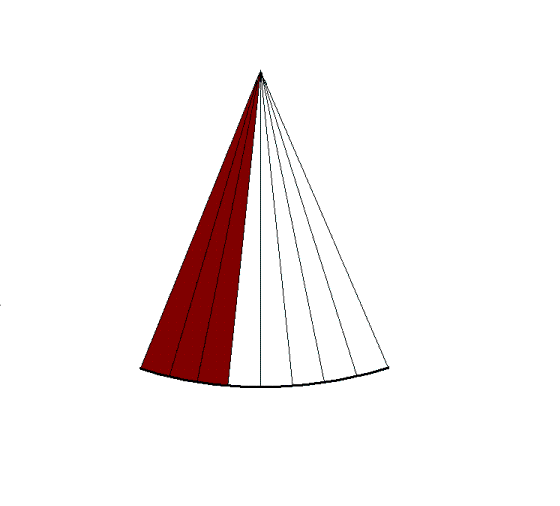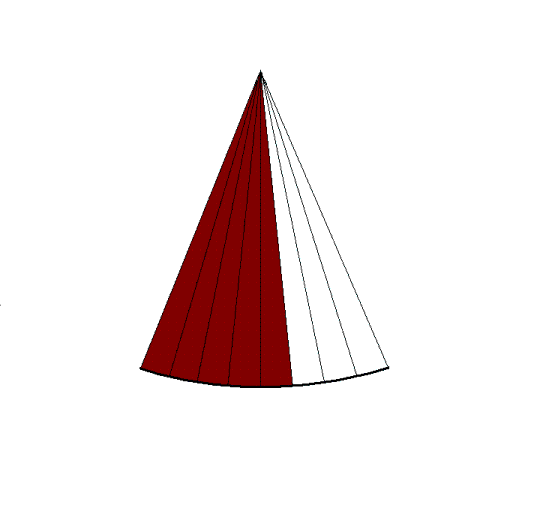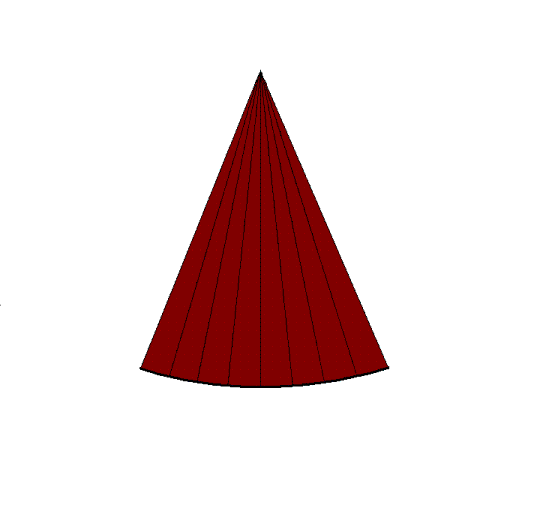
In a sector angle, the line density falls with distance from the probe, as the lines diverge.

However, as the beam width also increases at depths greater than the focal depth, the ideal line density for a sector probe is the one where beam distances are equal to the beam width at the focal depth. This will give the best lateral resolution. A line density that is so high as to make lines overlap, will not result in increased lateral resolution. A line density that leaves gaps between the lines, will have less than optimal lateral resolution as determined by the probe aperture and focal depth.

But as the time it takes to build each line in the image for any given depth that is desired, the number of beams in an image limits the frame rate. And if a greater sector width is desired without reducing the frame rate, the line density is reduced (same number of lines over a wider angle).

Thus, the line density itself is limited by other factors as well:

Frame rate (including the depth).
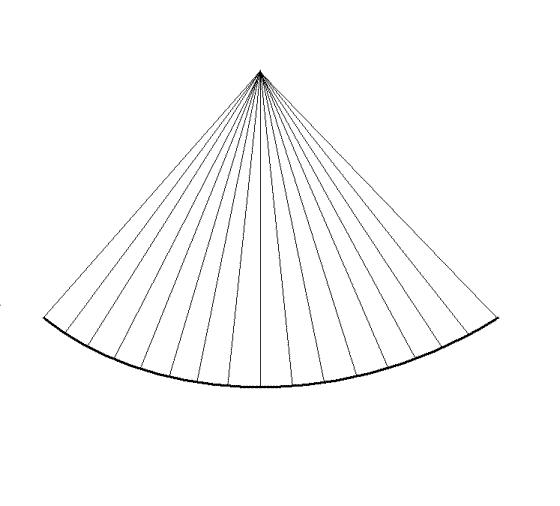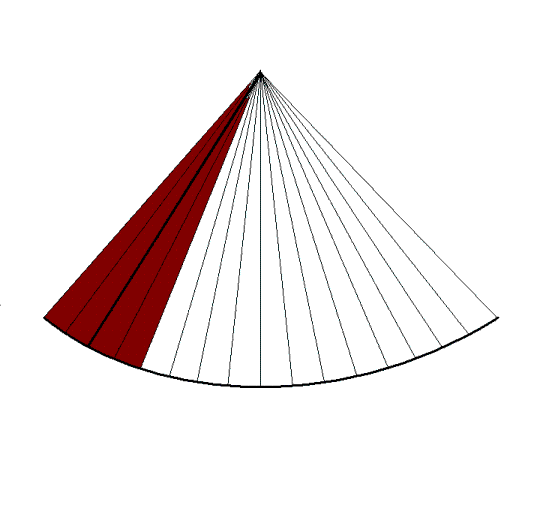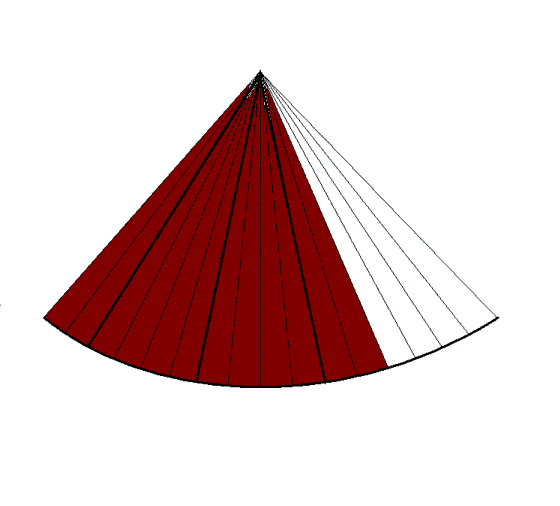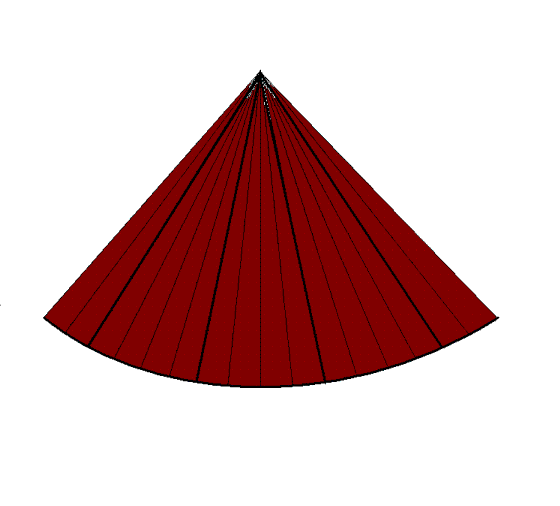
Sector width. Increasing sector width has to be compensated either by lower frame rate or by lower line density (keeping the same number of lines in a wider sector) as shovn below.
Depth in sector. As the sector width is increasing by depth, lines diverge, and the line density falls correspondingly.

Due to these factors, the line density often falls below the theoretically desirable described above, and the line density, not the probe size and wavelength becomes the limiting factor for the lateral resolution.

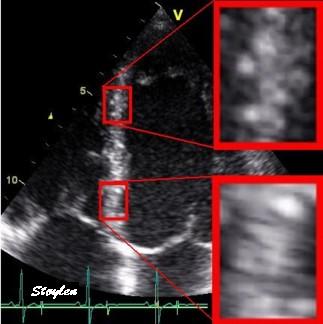
Two different lateral resolutions, the speckles can be seen to be "smeared". In this case the loss of resolution in the right image is due to lower line density . By rights the image should appear as split in different lines as indicated in the middle, as each beam is separated, line density being less than optimal relative to the beam width. Instead the image is interpolated beween lines. This reduction in line density is done to achieve a higher frame rate, as illustrated below.

So a distinction should be made between the lateral beam resolution, given by the fundamental properties of the system, and the image resolution that is a compromise between the requirements of frame rate, angle width and depth.

The discussion may be extended, taking all issues into consideration:


A: Beam width. Speckles (true speckles: black) are smeared out across the whole beam width ( Apparent speckles dark grey, top). This means that with this beam width the speckles from to different layers cannot be differentiated, and layer specific motion cannot be tracked.	B: Line density. Only the lines in the ultrasound beams (black) are detected, and can be tracked, beams between lines are not detected or tracked. The spaces between lines cannot be seen in the final image due to image lateral smoothing.	C: Divergence of lines in the depth due to the sector image will both increase beam width and decrease line density in the far field. this may result in the line density and width being adequate (in this example for two layer tracking) in the near field, but inadequate in the far field, situation there being analoguous to A.	D: Focussing. The beams being focussed at a certain depth mau mean that line density may be inadequate at the focus depth. Thus speckles in some layers may be missed. IN general, the default setting will usually give the best line density at the focus depth, so unless frame rate is increased, this problem may be minor. Howewever, line density will decrease ifalso if sector width is increased, there is a given number of lines for a given frame rate and depth. In any case, in the far field, the beams will be broader, and the beam width will be more like A and C.	E: Focussing may even result in beams overlapping int the far field. A speckle in the overlap zone may be smeared out across two beams.

Thus, the line density can be increased by

Reducing the sector width (gives higher line density by spreading the lines over a smaller angle)
Reducing frame rate (enables time for builing more lines between frames)
Reducing depth (enables a higher line density for a given frame rate, as the shorter lines takes shorter time to build).

This is discussed in detail below:

Temporal resolution (frame rate):

To imagine moving objects, structures such as blood and heart, the frame rate is important, related to the motion speed of the object. The eye generally can only see 25 FPS (video frame rate), giving a temporal resolution of about 40 ms. However, a higher frame rate and new equipment offers the possibility of replay at lower rate, f.i. 50 FPS played at 25 FPS, which will in fact double the effective resolution of the eye.

In quantitative measurement, whether based on the Doppler effect or 2D B-mode data, sufficient frame rate is important to avoid undersampling. In Doppler, the frame rate is also important in the Nykvist phenomenon.

The temporal resolution is limited by the sweep speed of the beam. And the sweep speed is limited by the speed of sound, as the echo from the deepest part of the image has to return before the next pulse is sent out ad a different angle in the neighboring beam.

Depth

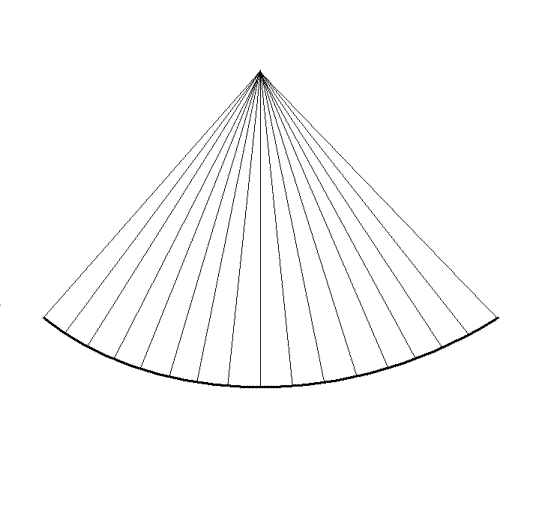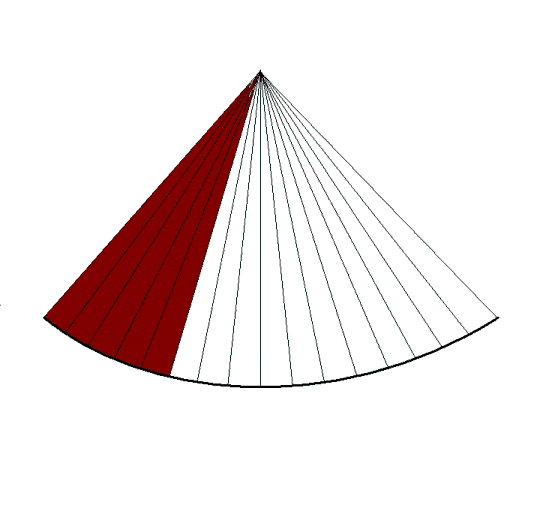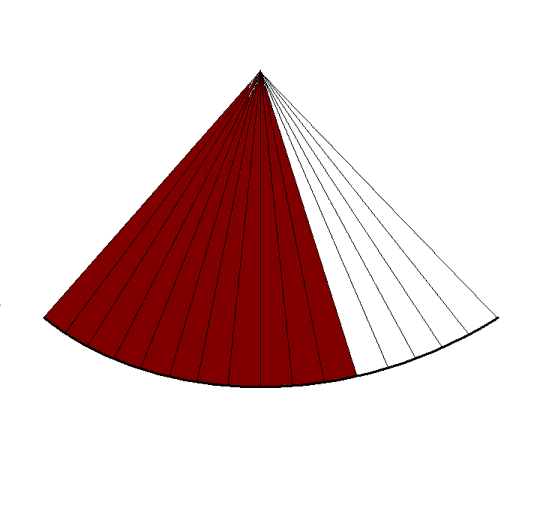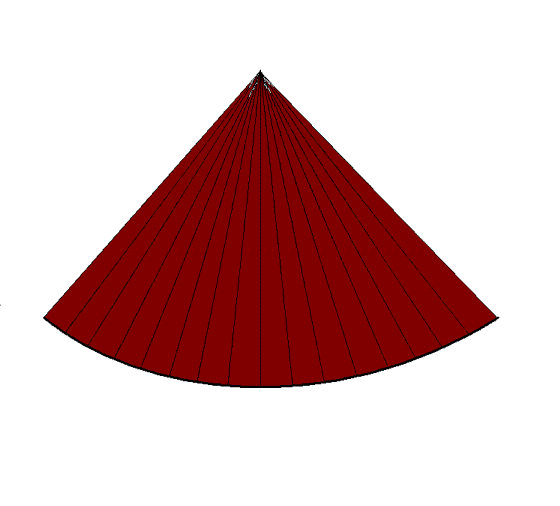
If the desired depth is reduced, the time from sending to receiving the pulse is reduced, and the next pulse (for the next beam) can be sent out earlier, thus increasing sweep speed and frame rate, as shown below.


As the depth of the sector determines the time before next pulse can be sent out, higher depth results in longer time for building each line, and thus longer time for building the sector from a given number of lines, i.e. lower frame rate.	Thus reducing the desired depth of the sector results in shorter time between pulses, and thus shorter time for building each line, shorter time for building the same number of lines, i.e. higher frame rate. In this case, the depth has been halved, and the time for building a line is also halved.

For a depth of 15 cm, this means that the time for building one line will be 2 x 0.15 m / 1540 m/s = 0.19 ms. The frame rate is then given by the depth and the number of lines, which again is a function of sector width and line density. Thus, for 64 lines the time for a full sector will be about 12 ms, which in theory may give a frame rate of around 80 FPS, in practice the frame rate is lower, around 50.

The point of this, is that reducing the depth to the field of interest will give a higher frame rate, that can either be used for higher temporal resolution, or for increased spatial resolution or sector width (see later). Looking at commercial scanners, the effect of reducing depth is often surprisingly little, this may be due to the manufacturers automatically using the increased temporal capacity to increase line density rather than frame rate.

Still, the field of view should be limited to the field of interest. In practice, when studying the ventricles, the atria should be excluded.


In this case, in the image to the left, the depth has been halved, reducing the time for building each line to half, thus also reducing the time for building the full sector, increasing the frame rate.

Number of beams: Sector width and line density.

The sweep speed can also be increased by reducing the number of beams for a full sector. Reducing the number of lines in the image will reduce the time for building up the whole image. This can be achieved by either decreasing the sector angle (width), but keeping the line density, i.e. reducing the field of view but keeping lateral resolution. Decreasing the line density, but keeping the same sector angle will achieve the same increase in frame rate, but reduce lateral resolution.


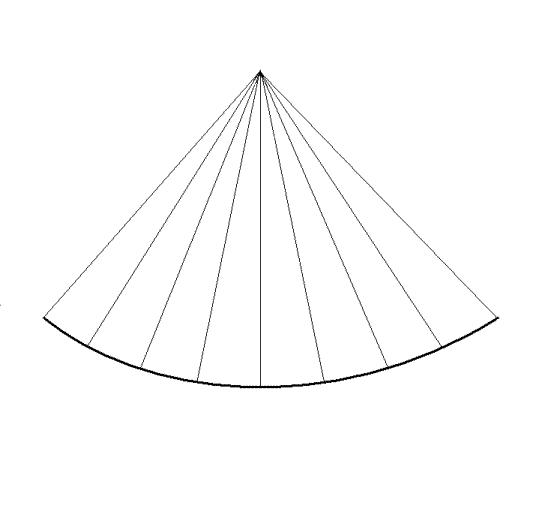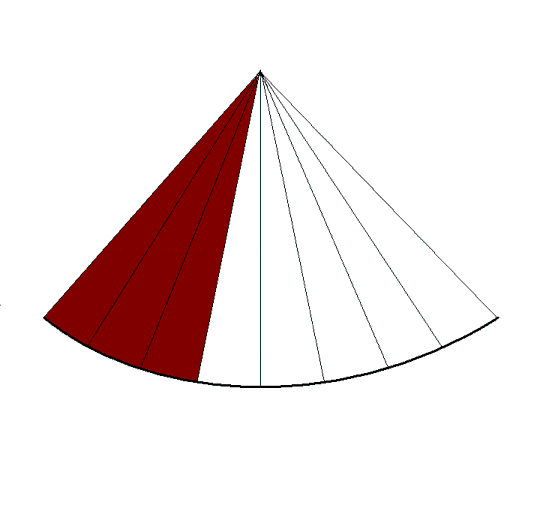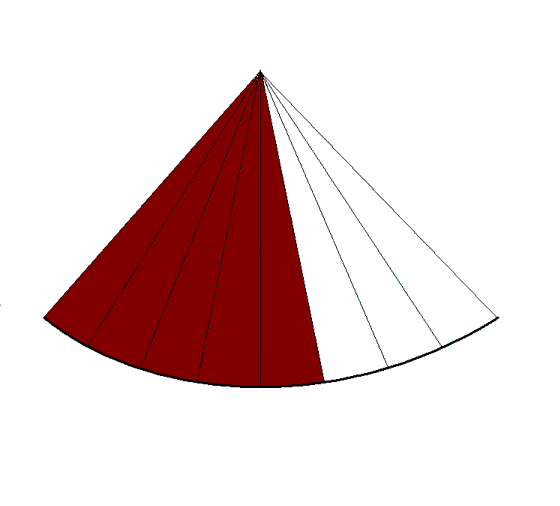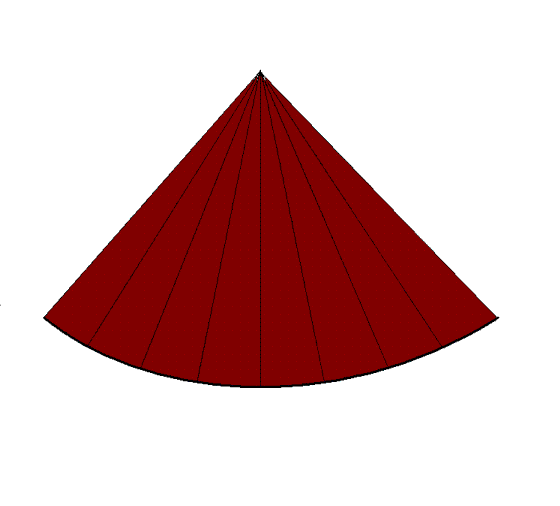
A sector with a given depth, sector width and line density determines the frame rate.	Reducing sector width, but maintaining the line density, gives unchanged lateral resolution but higher frame rate, at the cost of field of view.	Reducing the line density instead and maintaining sector width, results in lower number of lines, i.e. lateral resolution, and gives the same increase in frame rate.

Ultrasound acquisitions of the same ventricle at frame rate 34 ( left), 56 (middle) and 112 (right), all other setting being equal. Increased frame rate is achieved by reducing the number of lines; i.e. the line density. This can be seen as an increasing width of the speckles in the image with increasing frame rate, resulting in a lateral blurring of the image. The first step from 34 to 56 seems to retain an acceptable image quality, indicating that the line density was redundant at the lowest frame rate. ( In fact, it may seem that the image in the middle has the best quality, as the left image seems more grainy. But the graininess is the real appearance of the echoes, while the more homogeneous appearance in the middle and the left is due to smearing). However, as line density decreases toward the bottom of the sector (by the divergence of the lines), the effect is mos clearly seen here, i.e. in the atrial walls, the mitral ring and valve. In the image to the right, the endocardial definition is lost. As it is the echoes that are smeared, the effect will result in an apparent decreased cavity size.

These images also illustrates the drawback of time gain compensation, all three images has the same TGC, showing about the same brightness of the walls from base to apex, (the attenuation being offset by the TGC), but with increasing cavity noise.

Multiple line acquisition (MLA)

However, a method for increasing the frame rate for a given sector and line density, is to fire a wide transmit (Tx) beam, and listen on more narrow receiver (Rx) beams (crystals) simultaneously. This is called multiple line acquisition (MLA), and is illustrated below:

In this example, a wide beam is fired, and for each of the four transmit beams, there are four receiver beams (4MLA). thus, the frame rate is increased fourfold for the same number of lines.

Limitations of the MLA technique

The MLA has limitations that are especially important in forming the B-mode image.

A wider beam has a smaller transmit aperture. This reduces resolution.
Transmit beams have to be less focused, as they have to cover the field for the whole depth. This results in less penetration.
Increased noise from side lobes.
Angle discrepancy between transmit and receive beams. The higher the MLA factor, the more angle discrepancy in the latearal field of the transmit beam.

Especially the last point will result in MLA artefacts, that are visible as longitudinal lines of blocks in the B-mode image as shown below:

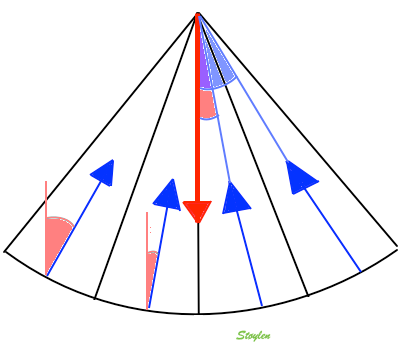
MLA angle discrepancy. The width of one transmit beam is exaggerated for visualisation. One wide beam is transmitted, and four narrow recieve beams. The transmit beam has has a main direction shown by the red arrow. The receive beams has directions (blue arrows) with an angle to the transmit beam, and this angle increases with increasing distance of the receive beam from the middle of the transmit, i.e. with the MLA factor.

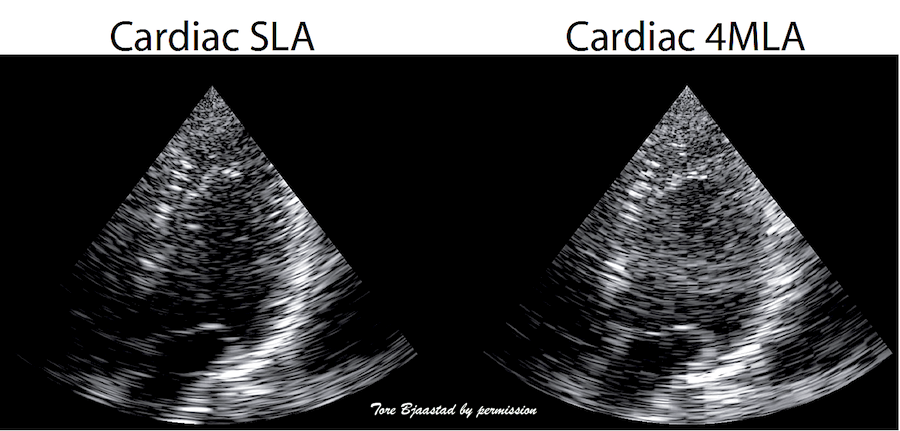
MLA angle artefacts in B-mode. Left: single line acquistion, where frame rate is acquired by a fairly low line density, and the image is then smoothed with interpolation between scanlines as described above, right, 4MLA acquisition. This should in principle result in a quadrupling of the number of lines, and an image with better lateral resolution. However, the increasing angle deviation between the Tx beam and the RX beams in the lateral parts of the Tx, will result in the lines being visible as blocks, the improvement in image quality being negligible or none. Image courtesy of Tore Bjaastad.

Image smoothing this in the image will result in "smearing", and hence, reduced resolution again. Thus, increasing frame rate with MLA and then smoothing the image, becomes similar to increasing frame rate by reduced line density. Thus, in B-mode, where image quality is the main focus, there has been a practical limitation of 2 MLA.

In tissue Doppler, the image quality is of less concern, as the main emphasis is on velocity data, rather than image quality. Thus, the MLA factor, and hence, the frame rate of tissue Doppler is thus usually higher, but at the cost of lower lateral resolution. This may not be apparent, unless one compares data across the beams. An example can be seen here. In practice, the MLA factor can at least be increased to 4 MLA.

However, modern equipment will allow more data to be transmitted directly into the scanner, and modern computer technology allows more data processing at higher speed. Thus, technology will become far more complex, and neither traditional beamforming nor image processing conforms to the simple principles described here, but they will still serve to give an idea. And the physical principles still apply.

In practice, for modern B-mode, frame rates will become similar to colour tissue Doppler, when the MLA artefact preoblem is dealt with.

3D ultrasound

3D ultrasound increases complexity a lot, resulting in a new set of additional challenges.

The number of crystals need to be increased, typically from between 64 and 128 to between 2000 and 3000. However, the probe footprint still needs to be no bigger than being able to fit between the ribs. And the aperture size must still be adequate for image resolution.

The number of data channels increases also by the square, from 64 to 64² = 4096. This means that the transmission capacity of the probe connector needs to be substatially increased, and some processing has to take place in the probe itself to reduce number of transmission channels. .

The number of lines also increase by the square of the number for 2D, given the same line density, meaning that each plane shall have the same number of lines, and a full volume then shall be n=built by the same number of planes. This means that given 64 lines per plane, the number of planes should be 64, which means a total of 64 x 64 = 4096 lines. This means that the frame rate (usually termed the "volume rate" in 3D imaging), will be 0.19 ms x 4096 = 778 ms, or about 0.8 secs. Meaning about 1 volume per heartbeat for a heart rate of 75. This is illustrated below.

Building a 2D sector with lines. (Even though each line (and the sector) has a definite thickness, this is usually not considered in 2D imaging, except in beamforming for image quality.

Building a 3D volume. Each plane has the same number of lines as in the 2D sector to the left, and takes as long to build. The number of planes equals the number of lines in each plane. Here is shown only the building of the first plane (compare with left), but the time spent on each of the following planes are in proportoion. The time for a full volume is then equal to the square of the number of lines in each plane.

This means that full volume 3D ultrasound has to pay a price of a substantially reduction in both frame rate and line density (resolution) at the same time. Thus, the lateral resolution is poor in 3D acquisition compared to 2D acquisition. The images can be seen to be very smoothed, compared to 2D.

Possible compensations are:

MLA technique, as the MLA gating will reduce the time used for each plane, and if used in both coordinates (lateral and azimuth) it will reduce the time by the square of the MLA factor. Thus 3D 4MLA is equivalent to 2D 2MLA, 3D 16MLA is equivalent to 2D 4MLA. But as discussed above, increased MLA factor will need smoothing to compensate for MLA artefacts, and thus increased volume rate is achieved at the cost of resolution. This is very evident in 3D echo from vendors who offer 16 mLA, images are extremely smoothed. Thus, even if some vendors have a high frame rate, images can be seen to be very smoothed, while others have maintained a better resolution, but at the cost of very low volume rate, often down to 5 VPS. This has to be compensated, for instance by stitching.

Gated acquisition (stitching). In ECG gated mode, only a part of the sector is taken in one heartbeat, allowing a higher line density as well as higher number of planes in the partial sector. Next part of the sector is than taken in the next heartbeat, and the two volumes are aligned by ECG gating. This is illustrated below.

Gated volume acquisition (stitching). In this case of four heartbeats. Only one fourth of the full volume is taken in one heartbeat, so the full heartbeat is used for increased number of lines and planes, as well as shortening the time for the acquisition of the partial volume. In the next heartbeat, the next fourth of the volume is acquired, and so on acquiring a full volume in four heartbeats. The four partial volumes are then aligned by ECG gating into one reconstructed volume, and the reconstructed volume thus has the same volume rate as the four partial volumes.

Thus, the limitation in 3D sector size can be used both for more lines (resolution) and increased volume rate. However, the reconstructed acquisition is no longer real time.
Volume acquisition can then be displayed as either a surface rendering, or multiple section planes through the volume:


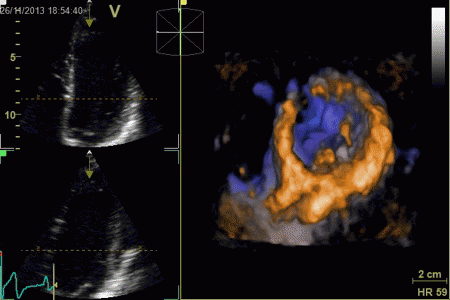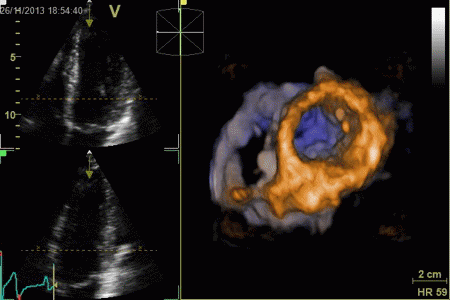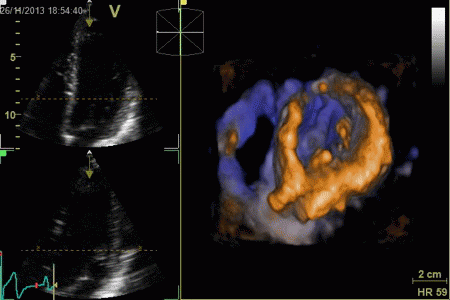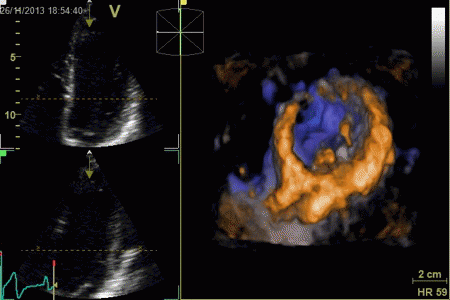
Surface rendering of a 3D volume. The image shows a cut through the LV between base and apex, looking down toward the base, the papillary muscles and mitral valve can be seen. The illustration also shows that the temporal resolution is to low to actually show the opening of the mitral valve during trial systole, only a slight flicker can be seen at end diastole.	The same volume, now displayed as a series of short axis slices from apex (top left) to base (bottom right). A slight stiching artefact (spatial discontinuity) can be seen in the anterior wall (top of each slice).

The rendering is mainly useful for morphology, especially valves, but here, TEE gives better images. The short axis slices are more useful in assessing wall motion.

Display of morphology, especially mitral leaflets (resolution not good enough for aortic from the apical position), this is vastly improved by 3D TEE.
Volume measurement. A good 3D volume eliminates foreshortening that may be masked by moving the probe in separate 2D planes. Some studies have shown better validity and reproducibility by 3D than 2D, although poorer feasibility.
Regional wall motion assessment, especially in the base. Basal segments may move due to tethering, even if there is no intrinsic function. On the other hand, normal segments may display apparent dyskinesia die to out of plane motion, especially in the inferior wall. Assessing wall motion in cross sections, is visually easier. Also, wall thickening, as different from wall motion, may be easier to see in the cross sections.

The disadvantage of this is that each full-volume heart cycle is constructed from multiple beats, and small movements, f.i. by respiration, may result in mis alignment of wall segments. The acquisition is thus usually taken in a breathold, and thus there is a practical limitation to the number of beats that can be stitched. Usually four to six are used, six being at the limit for many patients. Four beats, by most vendors now will result in a volume rate of around 20 VPS.

Any small movement will result in mis alignment of the sub volumes, with a sharp boundary within the volume where there is both spatial and temporal discontinuity (stitching artefact).

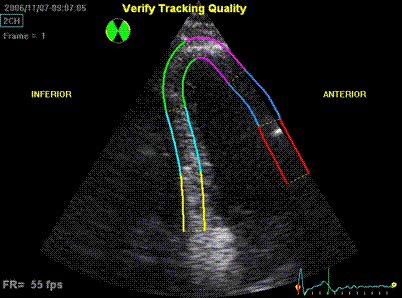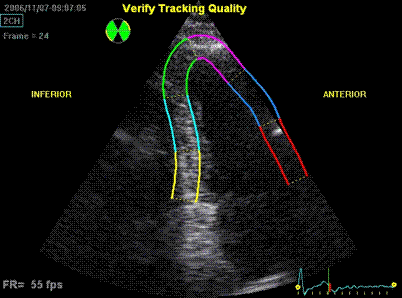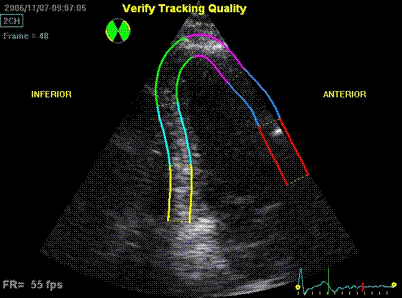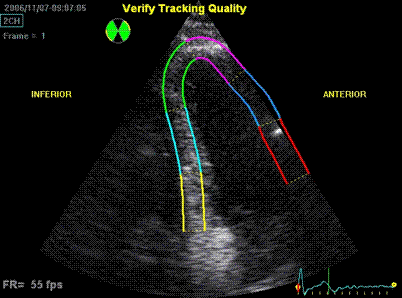
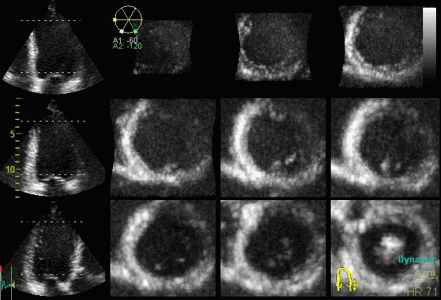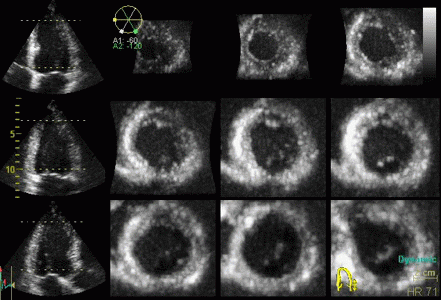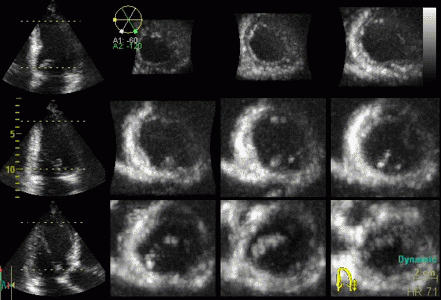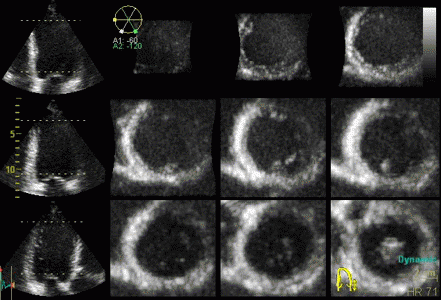
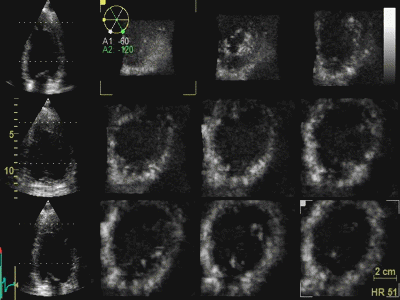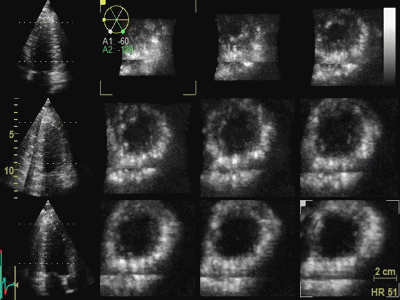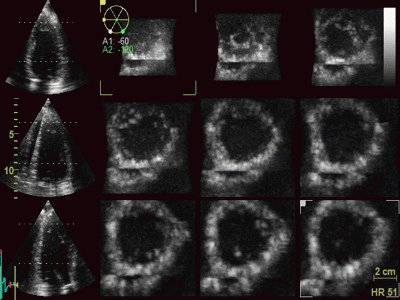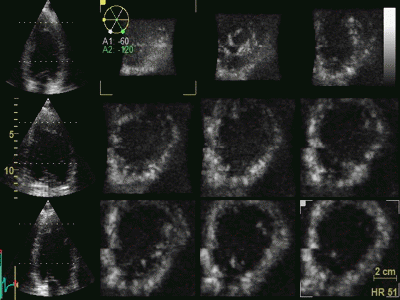
3D acquisition of a ventricle with inferior infarct. The display is shown as the apical planes to the left, and nine cross sectional planes to the right, going from the apex (top left) to the base (bottom right - reading order). The infarct can be seen as inferoseptal a - to dyskinesia in the basal sections. The image also illustrates that the software can be enabled to track the planes, thus eliminating out of plane artefacts when evaluating wall motion. Note that there is drop outs that cannot be eliminated by moving the imaging plane, in the anterior wall. Image courtesy of Dr. A. Thorstensen .

Styitching artefacts. In this volume, reconstructed from four heartbeats, i.e. four sub volumes, there are stitching artefacts between each of the sub volumes. This is due to motion of either the heart (f.i.) because of respiration, or of the probe. In the inferior wall (bottom of each slice), the spatial discontinuity is very evident, less so at the other stiches,, but in the anterior wall there is a discontinuity that illudes a dyssynergy.

Foreshortening

For correct display of the left ventricle, the imaging plane has to transect the apex. This is ensured by finding the apex beat by palpation. However, the apex does not necessarily offer the optimal window for imaging, and the intercostal space above may give a better view. However, this may lead to a geometrical distortion as illustrated below:

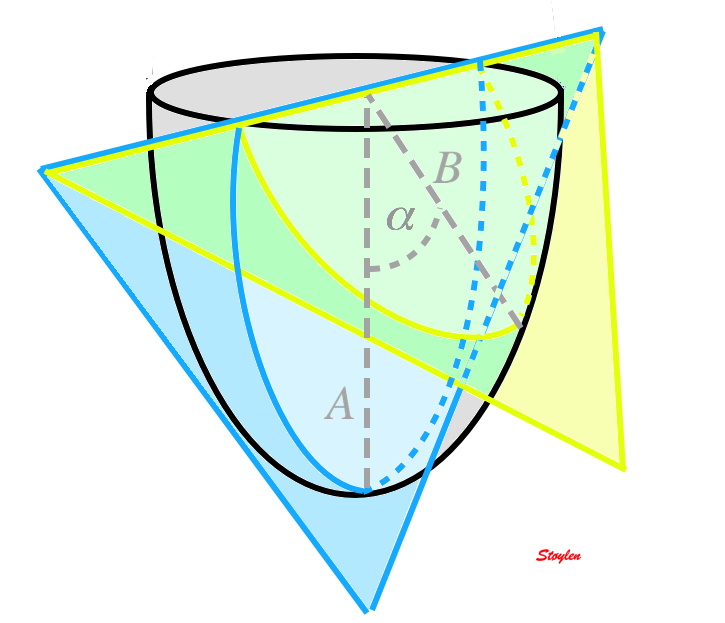Correct transapical plane (blue) versus foreshortened plane (yellow). Firstly, it is evident that the foreshortened plane excludes parts of the apical wall, but the foreshortened image still shows an ellipsoid figure, so the foreshortening is not immediately evident. There is an angle between the planes (), and the apparent longitudinal wall in the foreshortened image is actually partly circumferential.

This is shown in the images below:

Foreshortening. The three images are taken with identical gain, compress and reject settings. Left: correct apical position, showing the apex in the centre of the sector. The wall vivibility is poor. MIddle: by moving the probe one intercostal space higher, the wall visibility becomes much better. However, the ventricle canbe seen to be foreshortened, being much shorter than in the left image. But this is only evident by the comparison, without the reference image to the left, this is not apparent, as the (virtual) apex is in the centre of the sector. However, rotationg the probe to the two-chamber posisition, reveals that the apex in fact is not in the centre at all, thus the four chamber image is foreshortened.

The foreshortened image in four chamber view may seem to be better, at least for wall motion assessment, but the consequences may be:

Volumes and LV length will be underestimated (I've seen diagnosed bi atrial enlargement due to foreshortening simply because the normal atria looked bigger in relation to the foreshortened ventricle)
The apex is not imaged, and any apical abnormalities will be missed as seen below:

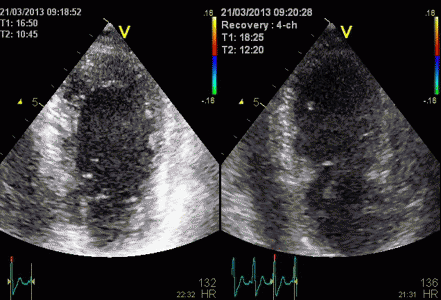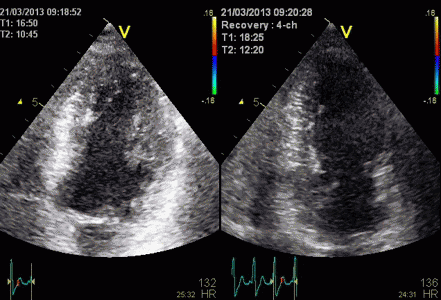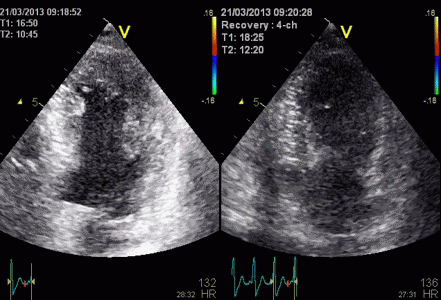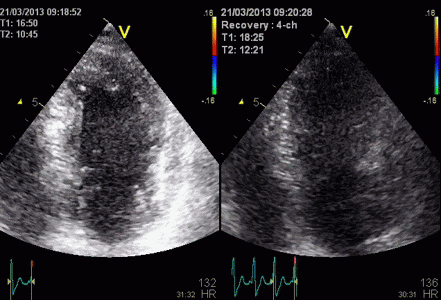Stress echo image at peak stress. The foreshortened image to the left shows good wall visibility, and apparent normal wall motion in all segments. Left: correct placement of the probe as seen by the slighty longer ventricle, shows poorer visibility, but the akinetic apicolateral part of the wall is evident, showing how foreshortening may almost totally mask any abnormality in the apex (Although some asynchrony may be seen).

Another example is shown below:

In this case, there is foreshortening in the four chamber view (left), which is not very evident. However, automatic adjustment of probe position when rotating to 2-chamber view (middle) and long axis view (left) masks the fact that there is foreshortening. The para apical position in the two latter views, however, is evident by the inward motion of the apical endocardium.

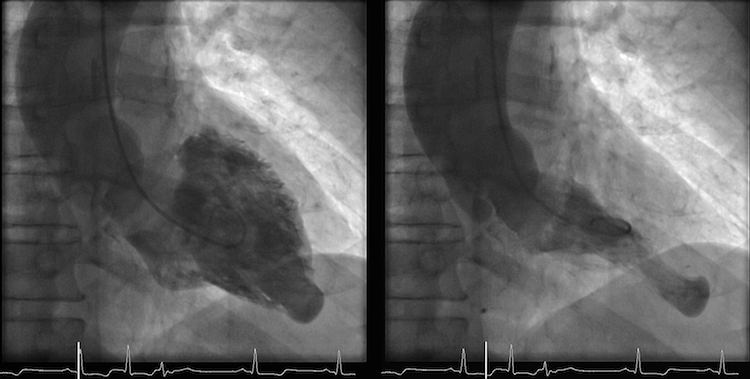
- and the apical aneurysm evident on this ventriculogram is missed.

The anterior wall is partly apical and partly circumferential. Thus longitudinal shortening, especially by speckle tracking may be circumferential rather than longitudinal. This may also be related to the curvature dependency of strain as measured by speckle tracking.

Non linear wave propagation and harmonic imaging.

Non linear propagation of the signal in the body, leads to distortion of the waves in the signal. But this again leads to a dispersion of the wavelength content in the signal, as assessed by Fourier analysis in the received signal.

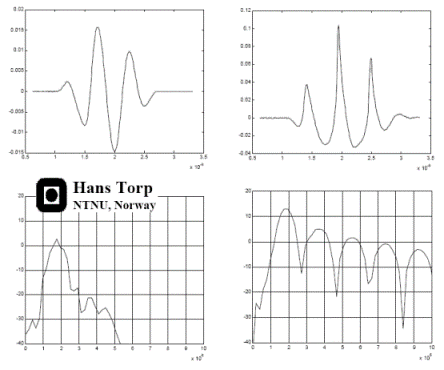Non-linear propagation. The upper panel shows the waveform of a pulse as originally transmitted, and after 6 mm transmission through tissue. The lower panels shows how the energy distribution is shifted to a more evenly distribution between more frequencies. (image courtesy of Hans Torp).

By Fourier analysis it is thus possible to send at half the frequency (typical 1.7 MHz as opposed to 3.4 MHz in native imaging), but receive at the same frequency (the second harmonic frequency: Twice the frequency is one octave higher). Thus, it improves penetration, which is important especially in obese subjects, while it retains the resolution (almost).

Fourier analysis of the resulting signal in native frequency (left) and second harmonic mode (left) shows that the native signal contains much more energy at all depth, while the harmonic signal contains most of the energy at a certain depth, in this case at the level of the septum, showing a much better signal-to-noise ratio.(image courtesy of Hans Torp).

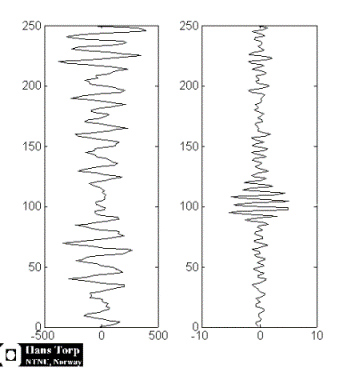
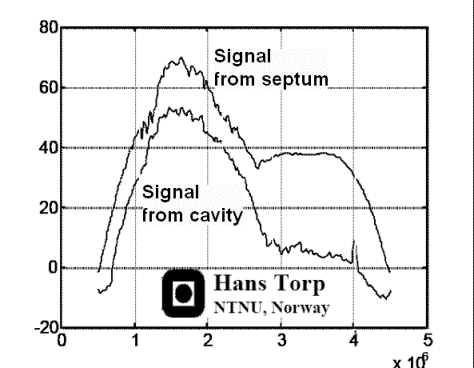
Energy distribution of the signal from cavity (lower curve) and septum (upper curve), showing the same phenomenon as the middle picture. The difference between cavity signal (being mostly clutter) and tissue is small in the native frequency domain (1.7 MHz), but there is little clutter at the harmonic frequency (3.4 MHz). Thus, filtering the native signal will reduce clutter, as shown below. (image courtesy of Hans Torp).

The noise from clutter and aberrations is mainly in the primary frequency, so the use of second harmonic will suppress noise, improving the noise-to-signal ratio. Also, the echoes from the side lobes are mainly in the primary frequency and will be reduced in second harmonic imaging.

Harmonic imaging, however removes all energy in the primary frequency. This means that there is an over all reduction in the reflected energy, even with improved signal to noise ratio. This means that there is limitations to how low it is possible to go in trnsmit energy (for instance i contrast echo). In addition, focussing is more important as this consentrates the energy in the beam.

Thus second harmonic imaging leads to:

1: Reduced noise and side lobe artifacts
2: Improved depth penetration.

Examples of the effect of harmonic imaging can be seen below.


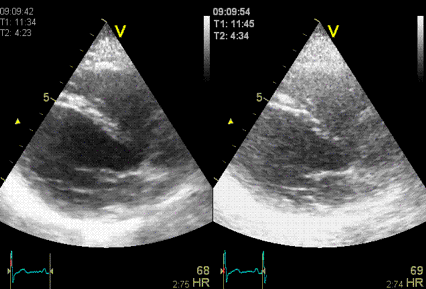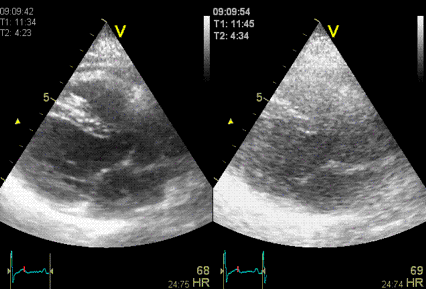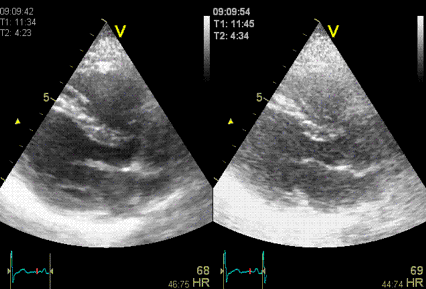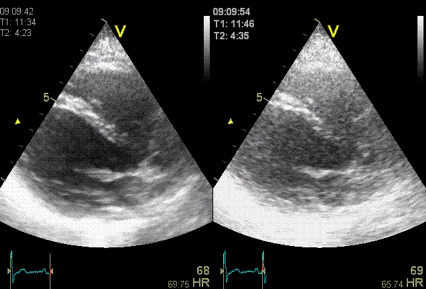
The same image in harmonic (left) and fundamental (right) mode, showing the improved signal-to-noise ratio in harmonic imaging, especially in rducing noise from the cavity. (Thanks to Eirik Nestaas for correcting my left-right confusion in this image text)	Stationary reverberation in harmonic (left) and fundamental (right) imaging, showing the effect of harmonic imaging on clutter.

However, due to the increase in pulse length with lower frequency, harmonic imaging also leads to:

3: Thicker echoes from speckles as discussed above.

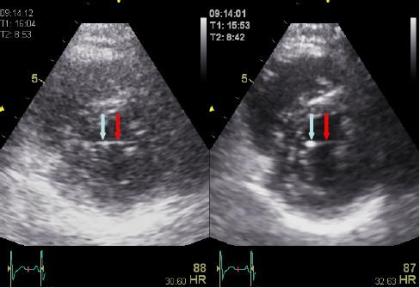
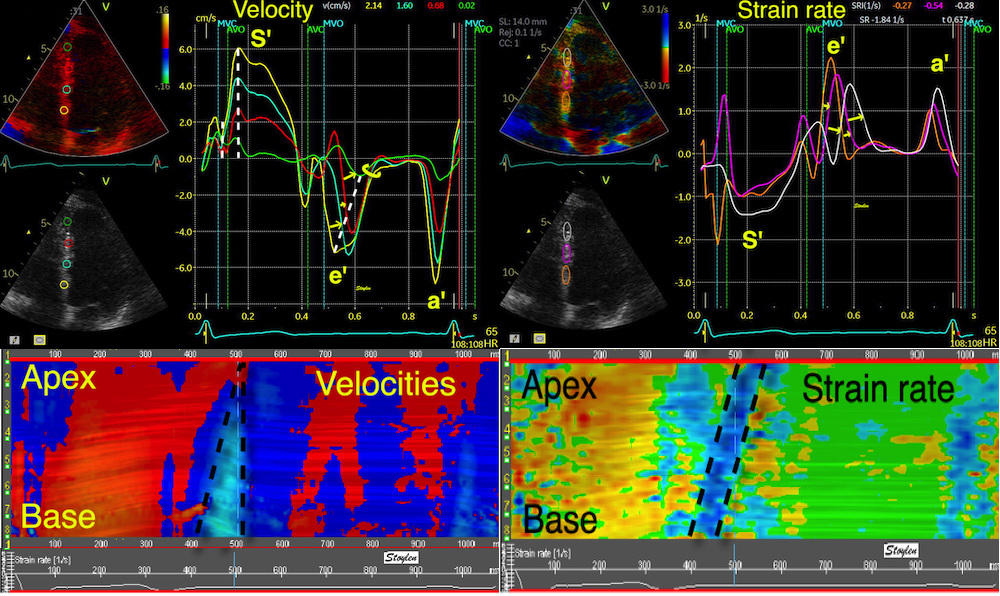
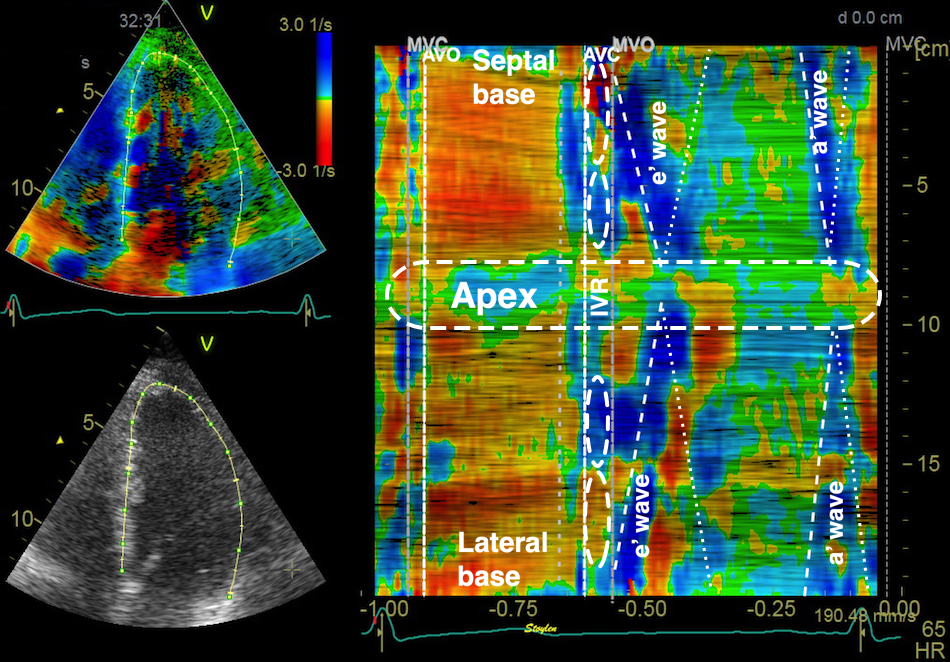
Fundamental (left) and harmonic (right) images of the left ventricle at the level of the chorda tendineae. The echo of the chorda (blue arrow) can be seen to be thicker in harmonic imaging, due to the longer pulse length. The echo generates a side lobe that can be seen to the right of the chorda. The side lobe is more prominent in fundamental than harmonic imaging. Note also the reduction in cavity noise from the right and left ventricle in the harmonic image.

Halving the transmit frequency will also halve the Nykvist limit, and thus is less suited to Doppler imaging as will be discussed below.

Methods for regional deformation measurement

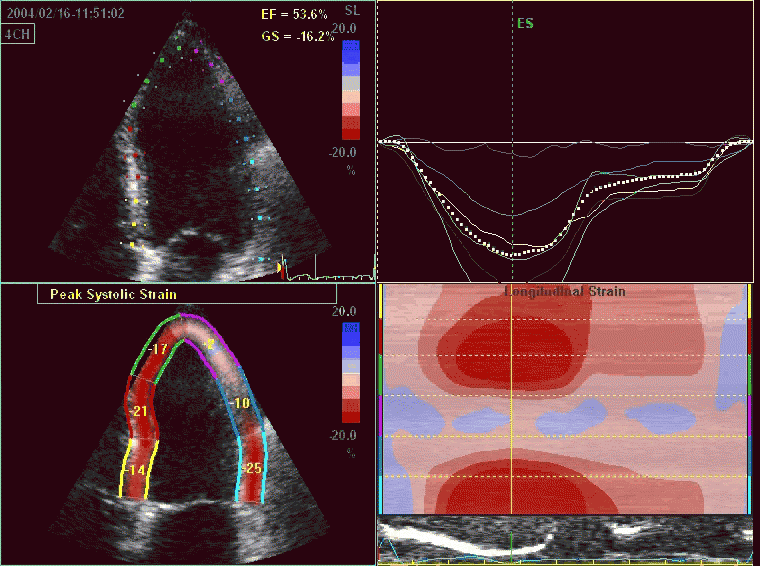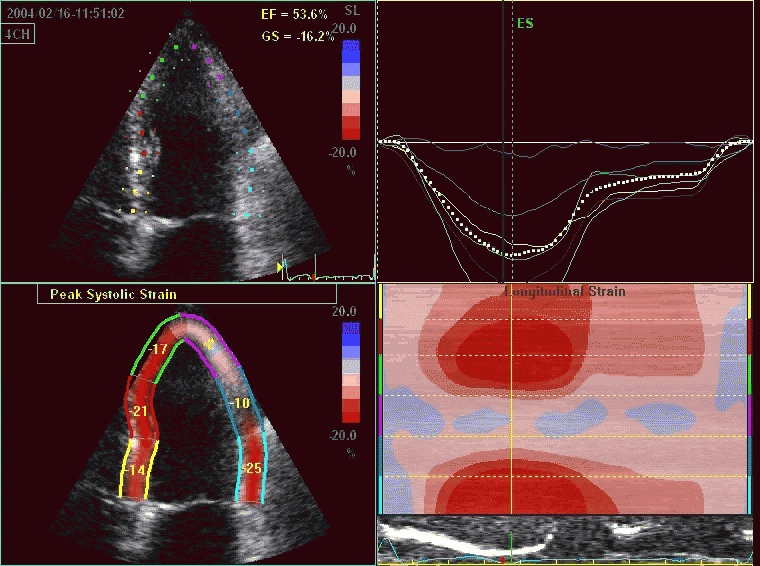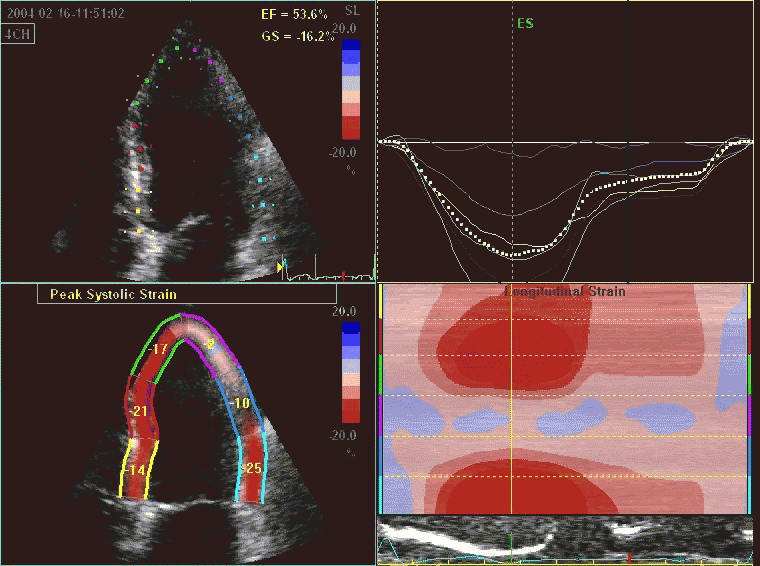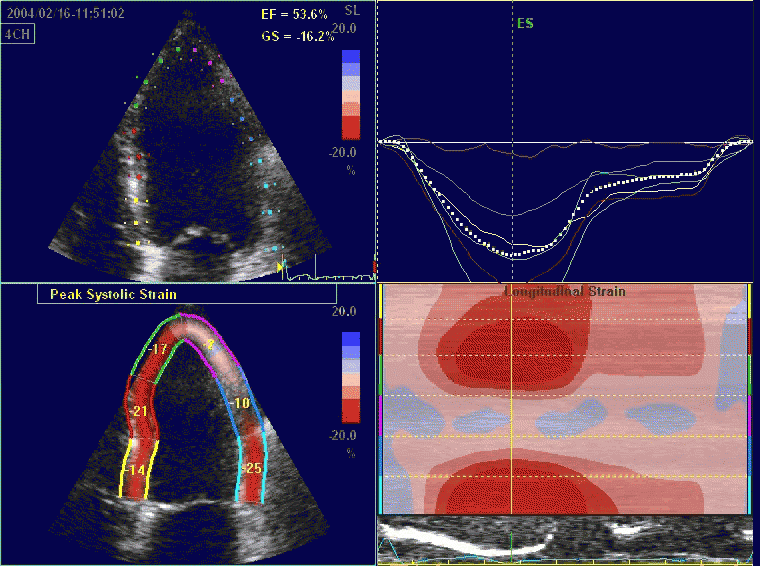
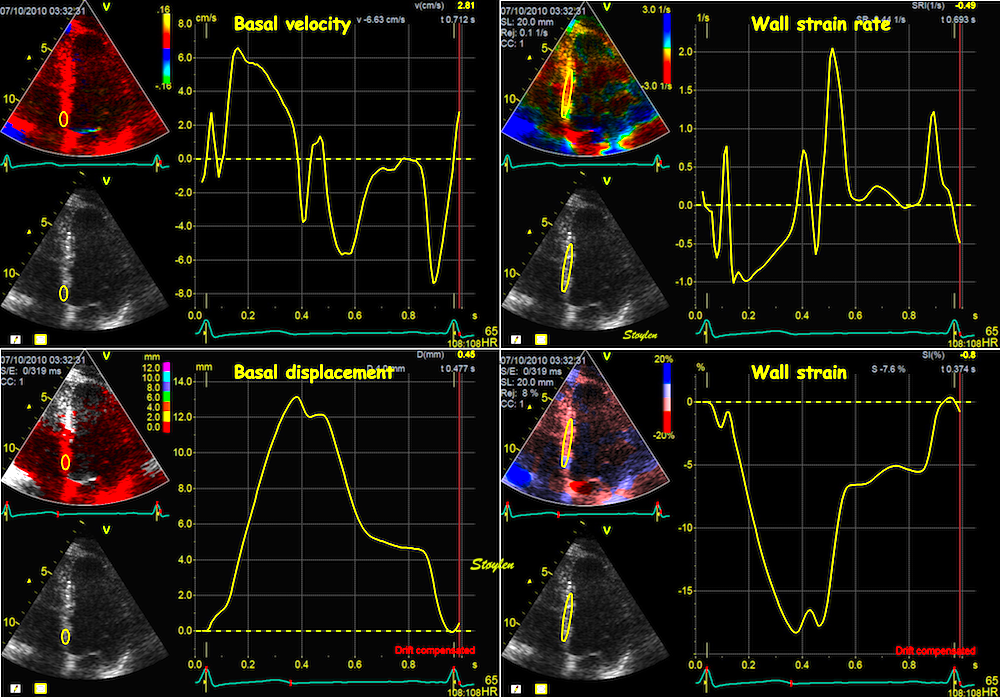
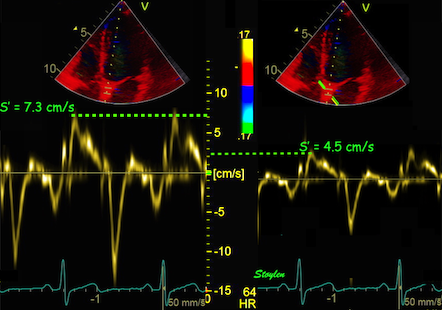
While global LV function can be assessed by longitudinal motion measures of the mitral ring; annular velocity (S') and annular displacement (MAPSE), both global and regional function can be measured byt the motion measures per length unit, strain rate and strain.

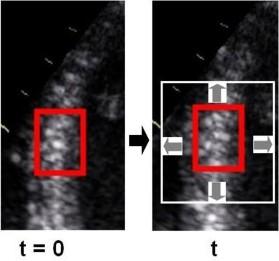
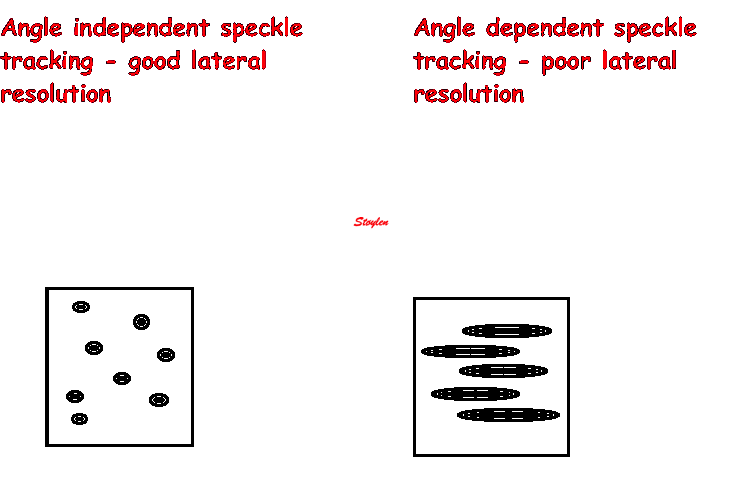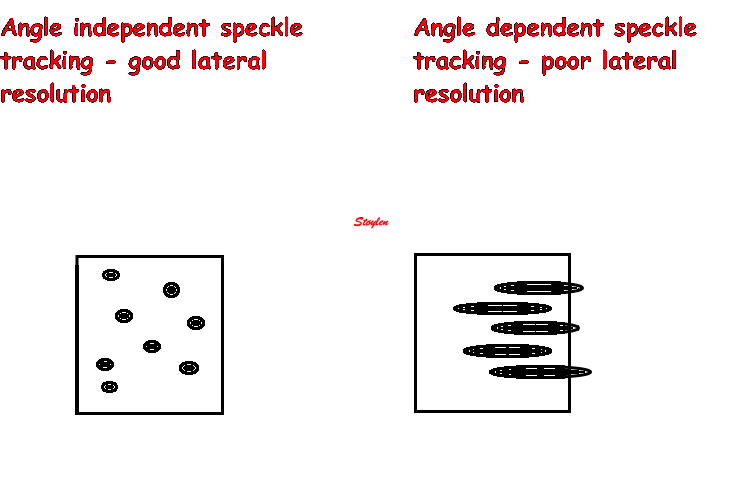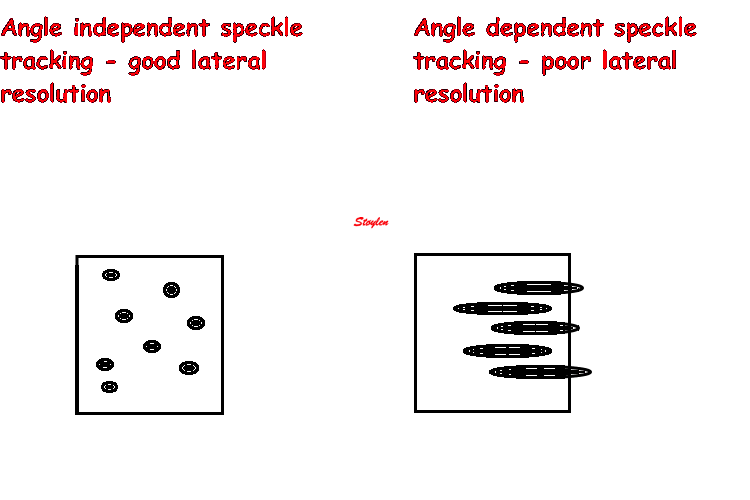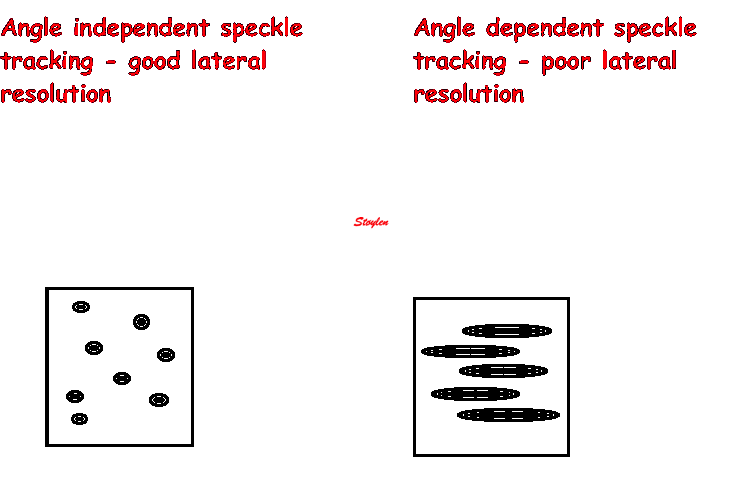
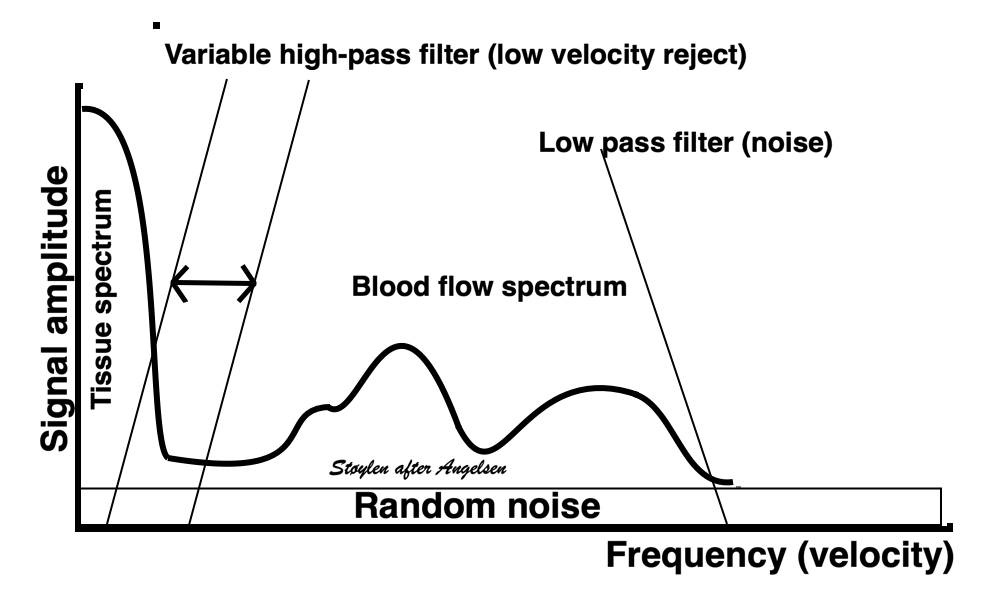
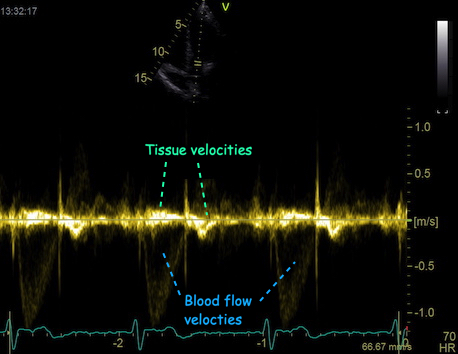
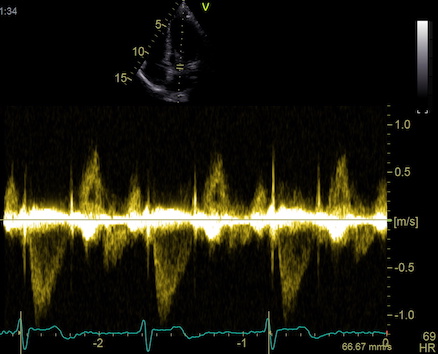
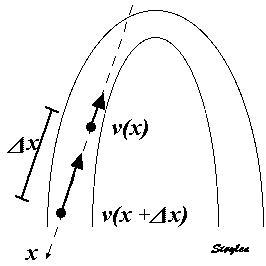
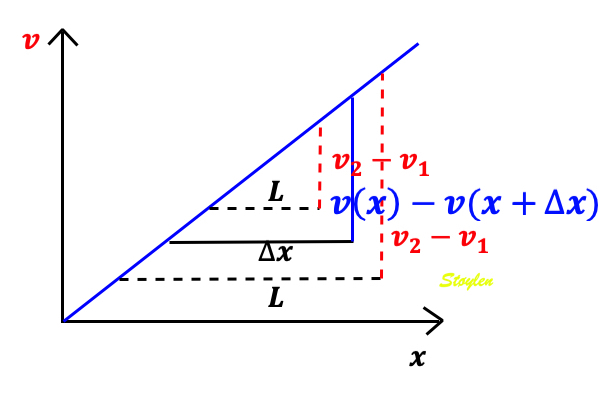
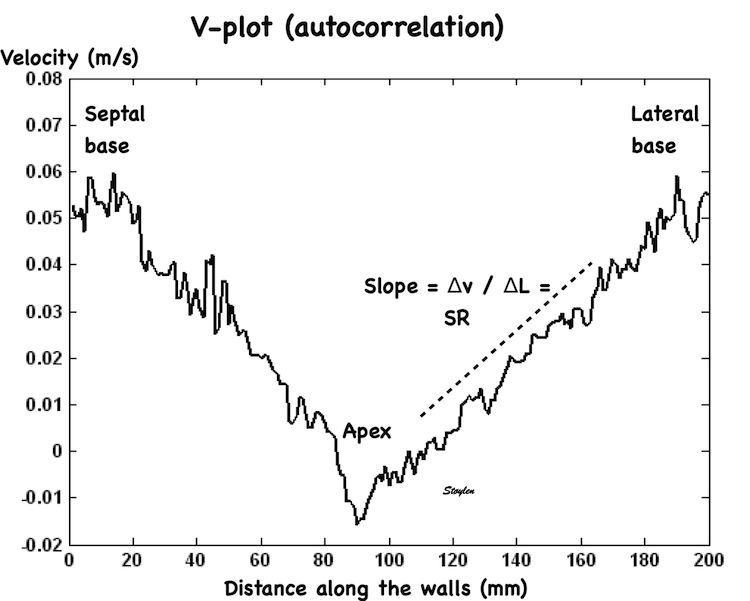
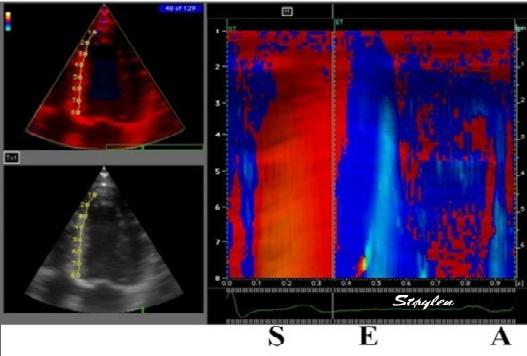
In order to asses regional motion, one has to access multiple (minimum two) measurements at different sites in order to do a spatial derivation of the difference, as explained in the basic concepts section..

In the present ultrasound the methods available for multiple sites motion measurement, are speckle tracking and colour tissue Doppler.

Speckle formation:

Speckle tracking

Lateral resolution in speckle tracking

This is dependent on both line width (being dependent again on frequency and focus depth), and line density (being dependent on frame rate and sector width). In addition, there has to be adequate alignment of the ultrasound beam, as angle deviation will reduce the number of lines within the wall in the far field. This is true for speckle tracking as well as tissue Doppler. Finally, focusing of the beams will result in different lateral resolution at different depths.

Speckle tracking has the advantage of a higher line density of B-mode, at the cost of a lower temporal resolution. The very low lateral resolution used in tissue Doppler in order to achieve a high frame rate, results in a low line density, and in practice limits the measurement in the beams in the longitudinal (and tangential - for circimferential measures) direction to the entire wall thickness, for a standard set up.

Lateral tracking in speckle tracking

Speckle tracking and angle dependency

Drop outs in speckle tracking

Reverberations (clutter) in speckle tracking

Reverberation in the lateral wall affecting speckle tracking. As is visually evident, the application does not track across the reverberation, thus the two segments apical to the reverberations are seen as akinetic, the basal as hyperkinetic. All shortening is seen in the basal segment. In this case, the smoothing is seen to spread the effect of the reverberation out across two segments apical to the reverberation.

Reverberations in segmental strain

Drift in speckle tracking

3D speckle tracking.

Doppler

Derivation of the Doppler equation

And thus

The time of one oscillation is the time it takes for the wave to move one wavelength is:


The Doppler effect for a moving source and a stationary observer. In the time the original wave has moved a wavelength (which is 1 / f₀), the source has moved the distance closer to the observer, determined by the velocity V of the source. The next wave will then meet the observer after the distance - , corresponding to the perceived wavelength .	The Doppler effect for a stationary wave source and a moving observer. In the time the wave has moved the distance , the observer has moved the distance closer to the source, determined by the velocity v of the observer, and will meet the wavefront earlier , corresponding to the perceived wavelength , which is - .
If the source moves toward a stationary observer with the velocity: In the time the wave moves one wavelength, the source moves the distance: The motion of the wave and the motion of the source happen during the same time interval (the time interval of one wave): The distance from the next wave emitted from the new position of the source (small dotted red circle) to the observer (blue) is shortened by in the direction of the motion, so the new wavelength representing the distance between the first and second waves is and thus: and: the change in frequency, the Doppler shift by the velocity of a moving source is: As we see, there is a difference between a moving source and a moving observer, but if v<< c, Then for a moving source: (The approximation is small, the velocity of ultrasound in tissue is 1540 m/s, while the velocity of blood is between 0,2 and 8 m/s, and tissue between 0.05 and 0.2 m/s, giving a v/c of maximum 0.005, i.e the approximation is maximum 0.5% and in reflected ultrasound 0.2%).	An observer (blue) moving towards a stationary wavesource with the velocity: will meet the wave as the wave have moved a distance , which is the perceived wavelength. The observer has moved the distance: The motion of the wave and the motion of the observer happen during the same time interval (the time interval of the perceived wavelength ), which is: The motion of the observer thus shortens the original wavelength by , , so the new wavelength representing the distance between the first and second waves is and thus: And the change in frequency, the Doppler shift by the velocity of a moving observer is:

For reflected ultrasound, the effect is twice as great. A reflector moving towards the source will shorten the incoming wavelength in the same way as an observer moving towards the source, and the reflected ultrasound wavelength will be further shortened in the same way as a moving source following the reflected ultrasound, Thus, the effect is:

so velocity can be calculated from the frequency shift of reflected ultrasound.

Continuous emission of ultrasound enables direct measurement of the return frequency, and thus the Doppler shift and velocity.

The emitted frequency is shown in blue, hitting a reflector. If the reflector moves towards the wave source, the frequency in the reflected signal will be higher (orange), if the reflector moves away from the source, the frequency will be lower (grey).

Spectral analysis

However, there will be more than one frequency in the reflected signal, due both to the bandwidth of the signal, as well as true dispersion of velocities (most important in blood flow Doppler).

Freque4ncy spectrum. The Doppler frequencies are distributed according to this frequency - amplitude diagram. Tissue echoes has high amplitude of the reflected signal, but low velocities (usually on the order of 1/10 of flow, resulting in low Doppler frequencies). Blood has higher, and more dispersed velocities with a wider distribution, and more varied, but lower amplitude.

Spectral Doppler from a patient with Aortic regurgitation. The image shows energy in a velocity range between -3 to +7 m/s, with energies distributed over the whole range. The random noise can be seen in the background, where there is no flow signal.

Frequencies can be resolveded by a method called Fast Fourier transform. Fourier transform of a wave is the method where a wave can be decomposed into sine waves with different wavelength (as described under harmonic imaging). Fast Fourier trasnsform, however, only decomposes the wave into the amplitudes of the different energies as illustrated below.

As described above, the reflected signal contains multiple Doppler frequencies, because the blood flow has multiple velocities. This is shown above, left ,exemplified by three velocities. Different amounts of the blood have different velocities, as indicated by the line thicknesses.Below. left, is shown the compound curve resulting from the three frequencies, which is the signal received by the probe. Fourier analysis can resolve the frequencies into different sine curves with different frequencies again. In this case is shown the fast Fourier transform, which only shows the amount of blood with eaqch frequency (by the amplitude), instead of resolving the full set of frequencies. The different amount of blood with each velocity is shown by different amplitudes of the signal.

Amplitude is displayed as brightness, in a manners similar to B.mode, while Frequency / Velocity are displayed on the y - axis and time on the x - axis. This results in the typical Doppler flow velocity curves:

Typical spectral flow curves. Left: Flow in the Left ventricular outflow, right in the mitral annulus. Velocities toward the probe (positive Doppler shift) are shown as positive velocities, velocities away from the probe (negative Doppler shift) are shown as negative velocities. The velocities are sampled at a certain depth by pulsed Doppler (see below). Thus, the velocity distribution is limited to a fairly narrow band. Note the absence of velocities near zero, due to the high pass filter.

At the same time, the amplitude is a function of the velocities, in pulsed Doppler, corresponding to the dispersion of the velocities in the sample volume.
as shown below:


Mitral flow, showing a fairly narrow spectrum band, indicating a relatively homogeneous velocity distribution within the sample volume, which is placed between the tip of the mitral cusps during filling, where the inflow jet is most narrow..	Pulmonary venous flow in the same subject, showing a wide distribution of velocities, within the sample volume placed in the right upper pulmonary vein. The sample volume is the same size.Venous velocities are much lower, but also varies from 0 to 0.5 m/s simultaneously.

Pulsed and continuous Doppler

Continuous vs pulsed wave Doppler. In continuous Doppler, one half of the aperture is dedicated sending, and one half receiving the reflected signal. Both signals are continuous, and all frequencies can be sampled continuously between each pulse from the overlap region. But the frequencies are received from all depths simultaneously, so there is no information about which depth the received signal originates. There is range ambiguity. The modality is best suited to measure peak velocities where they are high. Pulsed wave Doppler on the other hand, as shown below, uses the whole aperture for both send and transmit. A pulse package, consisting of at least two pulses is sent out, and the receive signal is sampled at a certain time, corresponding to a certain depth. The method shows the depth where the velocity corresponds to the spectrum. However, the pulsed modality results in a practical limitation in how high velocities that can be sampled, limited by the Nykvist phenomenon (aliasing) as explained below. Thus, pw Doppler shows velocity ambiguity above the Nykvist limit.

The width is the same as the beam width, and the length of the sample volume is equal to the length of the pulse.

Thus, in cw Doppler the sampling frequency equals the pulse repetition frequency. Continuous Doppler will measure all velocities along the ultrasound beam: The beam is transmitted continuously, and the received echoes are sampled continuously with no range gating. Thus, there is no information about the time interval from the signal to the reflection, and, hence, no information about the depth of the received signal; the signal may come from any depth. Cw Doppler will then sample all velocities in the sensitive region, irrespectively of depth, there is range ambiguity. The continuous Doppler has no Nykvist limit, and can measure maximal velocities. It is used for measuring high velocities.

As cw Doppler emits with one part of the transducer and receives with another, the direct analysis of the reflected frequency is feasible, and the velocity can be calculated directly from the Doppler shift.

Phase analysis

In pw Doppler, the analysis is done in terms of the phase shift: A wave can be described as a sine wave, and thus, any point on the wave can be described by which phase of the wave the point is. The phase of a point is represented as an angle. as illustrated below:



Phase analysis. If the waveform is treated as a sine curve, every point on the curve corresponds to an angle, and the phase of the point in the curve can be described by this angle; the phase angle . From the diagram, it's also evident that a full wavelength, , is equivalent to 2, and for every point the corresponding fraction of a wavelength is equivalent to an angle which is the fraction of 2.	However, from the diagram at the top, it is evident that by sampling the waveform only once, the phase is ambiguous, it is not possible to separate the phase of point a from point b. The two points are separated by a quarter of a wavelength, or 90° (). In order to determine the phase of the points unambiguously, the pulse has to be sampled at to points separated by less than a quarter wavelength. Then it can be seen that point a is in increasing phase from a₁ to a2, corresponding to a phase angle of 0 - /2 while b is in a decreasing phase corresponding to an angle of /2 - .

Shooting at least two (or more) pulses in rapid sequence, (NOT to be confused by sampling one pulse at two timepoints as illustrated above) results in the possibility to analyse the Doppler shift in terms of the phase shift between the pulses. The phase shift analysis is based on the principle that when pulse 2 hits a moving scatterer, the scatterer will have moved a little away from, or towards the probe, and the return pulse 2 will then be in a different phase from pulse 1. The distance the scatterer has moved, is, of course a function of the velocity of the scatterer and the time between pulses.

Two pulses sent toward a scatterer with a time delay

t = t2 - t1 = 1/PRF. Given that the scatterer has a velocity, it will have moved a distance, s, that is a function of the velocity and the time (s = v x

t). Thus, pulse 2 travels a longer (or shorter) distance equal to s, before it is reflected. During the time pulse2 has traveled the distance d to the new position of the scatterer and back to the point of the reflection of pulse 1, i.e. a distance 2d, pulse 1 has traveled the same distance away from the first reflection point, so the distance between the pulses have increased by 2s.

The pulses are emitted by a certain frequency, and the time between the pulses are

The distance one pulse travels in this interval before the emission of the next pulse is given by the speed of sound

But as seen above, a distance along a sine curve, is equivalent with a phase angle, and d as a fraction of a full wavelength equals the phase angle as a fraction of

If the two pulses are sent towards a moving scatterer, they will be reflected from the scatterer at two different times separated by an interval

, and in this interval the scatterer will have moved a distance given by the velocity of the scatterer

and this distance is traversed back and forth by the second pulse, as shown by the illustration above.

The time between the two pulses represent 1/PRF. The Doppler shift is very small compared to the ultrasound frequency. A velocity of 100 cm/s with a ultrasound frequency of 3.5 MHz results in a maximum Doppler shift of 2.3 KHz. The solution to this problem is shooting multiple pulses in the same direction and This results in a new signal with one sample from each pulse, the Doppler curve from this signal will be a new curve with the frequency equal to the Doppler shift.

A series of pulses shot successively. It is also evident the even without motion, there is a phase shift between pulses, but this is equal for transmitted and reflected ultrasound

Measuring the velocity of an object by phase analysis. The velocity of the scatterer is shown by the dotted red line, showing the phase in each pulse, and then the phase shift through the pulse package is illustrated by the full sinusoid red line shown to the left, where the troughs and peaks of the red line represents the scatterer's position at the peaks and troughs of each pulse, i.e. the phase in trelation to the twop pulses. In principle, the phase shift can be sampled between each pulse pair. The sinusoid curve is the phase shift curve, and the frequency is equal to the Doppler frequency.

The low frequency sinusoid curve represent the Doppler shift frequency, which again is proportional to the velocity, and the sampling frequency is thus equal to the pulse repetition frequency PRF.

Spectral analysis can also be done in Pw Doppler. Using more pulses per package, a spectral analysis can be resolved showing the distribution of velocities within the range window. Typically, this will be a spectral band of velocities, if the flow is laminar, while cw Doppler , showing all velocities at all depths will show the velocities "smeared out" over the whole range.


Cw Doppler signal from LVOT. The velocities can be seen to be present in all ranges, although the peak velocities are close to the curve shown by Pw Doppler to the left. The reason for the wider distribution, is that all velocities from the whole LVOT acceleration zone are displayed. In addition, a part of the mitral flow can be seen as well, showing that the overlap area of the two cw sectors is less well focused.	Pw Doppler signal from the same LVOT. Most of the velocities can be seen to be collected in a narrow band, roughly corresponding to the peak velocities of the cw Doppler. Also, there is less contamination from the mitral flow, as the sample volume (range gate) is in the focused part of the beam.	In pw Doppler flow, modal velocity is the middle of the band, and represents the mean velocity within the sample volume.

Using pulsed Doppler, the interval between the pulses can be used for updating the B-mode. However, this means that the B-mode pulses will interfere with the phase analysis at the start and end of the Doppler pulse, and reduce the signal quality of Doppler. In cw Doppler this will be even more pronounced. Thus, the signal will detorierate if B-mode is active, and the rule is to freeze B-mode when Doppler is acquired.

Signal quality with B-mode active and frozen. B-mode is frozen during Doppler acquisition, at the time of the white arrow, as evidenced by the break in the Doppler curve. The improvement in Doppler quality is evident.

Width of the spectrum

As can be seen from the illustrations above, the velocity spectrum has a certain width. In the blood, this partly reflects the spread of velocities between the multiple scatterers in the blood, i.e. the dispersion of velocities within the sample volume.

The width of the spectrum will also be influenced by gain.

Gain in Doppler


Pw Doppler recording from aorta descendens. Gain is set so high that the thermal noise is very visible. The main (modal) velocities is shown to be in a saturated band.	Same recording at low gain. The modal velocities is still visible, while the less intense velocities above that are not visible, and the band is narrower, thus the peak velocities will be slightly lower.

Mitral flow in high gain. Around the main spectrum is seen some noise spikes.	Same recording in low gain, removes noise spikes.

Which amount of gain to use is a question of the data that are interesting. In cw Doppler, the main issue is usually peak velocities (high velocities), so gain should be high enough to show these. This means gain should be high enough, not to loose the highest values, in practice the thermal noise should be visible. In pulsed Doppler that might be the case in vascular Doppler, where the peak velocities (in the centre of the flow), may have lower amplitude that the main bulk of the blood flow.

In cardiac ultrasound, this may differ. Often in flow through orifices, the Doppler is used to calculate volume flow, which means that the most interesting is the modal velocity, the main spectral band. As the width of this band may vary with gain as seen above, this means that gain should be as low as possible. Also this will reduce noise spikes, that may interfere with peak values. The width of the spectrum is especially important in tissue Doppler. There, the width of the spectrum is not due to velocity dispersion, but to bandwith, as explained in the tissue Doppler section. Thus, the middle of the spectrum is the representative value, and the width of the spectrum should be as low as possible. And as tissue velocities are about 1/10th of blood velocities, the error induced by the bandwidth is far bigger, relatively:

In this case, differences in gain leads to a difference of 3 cm/s in systolic peak values, and 3.5 cm/s in early diastolic peak values.

As said above, velocity dispersion is not the only explanation for the width of the spectrum.

Angle deviation in Doppler:

As described above, distances (e.g. wall thickness) and motion by M-mode) increases with increasing angle:

As a reflector moves from a to b in the direction 1, the true motion (displacement) is L₁. If the ultrasound beam deviates from the direction of the motion by the angle ,
the apparent length along the ultrasound beam will be L2, which is the hypothenuse of the triangle, and thus . Thus angle deviation of M-mode measures will always over estimate the real motion (as opposed to Doppler measurements).

The angle error in displacement measurement demonstrated in a reconstructed M-mode. Increasing angle between M-mode line and direction of motion increases the overestimation of the MAPSE.

The angle deviation will result in a change in the measured velocity by Doppler as well, but in this case the angle deviation results in an underestimation of velocity by the cosine of the angle.This is due to the fact that wavelength and frequencies are inversely related.

Left: distance along the axis x, imagined along the ultrasound beam y where is the angle between the direction of the motion and the ultrasound beam (insonation angle).

The angle effect is, as above:

This means that motion along an M-mode line will increase by the cosine of the angle deviation. Thus, the angle deviation gives an in which in reality is a decrease in wavelength, which in reality is a distance:

Frequency of ultrasound is the inverse of wavelength, so:

And thus from the special equation for reflected ultrasound given above:

and

so velocity can be calculated from the frequency shift of reflected ultrasound.

Vascular colour ultrasound. Left: Near 90° insonation angle, resulting in a weak signal and velocities close to zero by the colour scale. Left, angulation of insonation signals, resulting in higher velocities (compare the colour bar top, right) that are not removed by the clutter filter,. Image courtesy of Ingvild Kinn Ekroll.


Basically, the measured velocities decrease by the cosine function, being 0 at 90° insonation:	Angle distortion in Doppler. The image on the left has applied angle correction, and then adjusted to scale.This is only partly correct, the ange distortion will also broaden, not narrow the spectrum as shown here.

Angle distortion will thus decrease the Doppler velocity, but increase the bandwidth.

Angle correction:

If we know the true direction of flow, it is possible to correct the velocities by applying the cosine function. This means that the velocity will be multiplied by the cosine of the angle for all values. This is feasible, only if one knows the true flow velocity direction, as in vascular ultrasound. Here, there will always be an insonation angle, while the true direction can be assumed being parallel to the direction of the vessel. However, with increasing angle correction, the corrected angle will rise rapidly, and thus increase the possibility for errors in the correction:

Using angle correction, the coorrected velocities will increase by 1/cos(a), meaning that there will be extreme corrections at angles > 45°, and errors in the correction will increase too.

In intracardiac jets on the other hand, the jet direction is in general not known. As regurgitant or stenotic areas are small, compared to the chamber they enter, and the valves in addition being diseased (and hence, assymetric), the jets may in practice have any direction withinn a range of 180°. This means that the angle is unknown, and no angle correction can be estimated.

In intracardiac jets, the basic technique will be to use the probe to align with the flow, the best insonation will be the direction giving the highest jet velocities. Angle correction should not be applied!

Pw Doppler will only sample velocities at one depth. In pulsed Doppler, the pulse repetition frequency PRF is given by the sampling depth. A pulse cannot be sent out before the previous pulse has returned, so the pulse interval equals the time for a pulse to be sent to the sampling depth and back, with the velocity of sound. The Doppler shift is thus sampled once for every pulse that is transmitted. Thus, the pulse interval interval (PI) is given by the distance s = 2x depth, and the speed of sound c = 1540 m/s in soft tissue.

PI = 2d / c, and PRF = 1 / SI = c / 2d

This gives the maximum PRF at different depth:

Depth	SI	PRF
1 cm	0.000013s	77000 Hz
5 cm	0.00006s	15400 Hz
10 cm	0.00013s	7700 Hz
15 cm	0.00019s	5133 Hz
20 cm	0.00026 s	3850 Hz


Phase shift analysis. The distance between the pulses represent the pulse interval, or 1/pulse repetition frequency (1/PRF)	This means that the phase shift curve can be sampled only with a frequency equal to the PRF. Halving the pulse repetition frequency doubles the sampling interval. This results in the Doppler shift curve being sampled at half the number of pulses. This may result in velocity ambiguity as described below.	A more rapidly moving scatterer will then result in a higher frequency of the phase shift, i.e. a higher Doppler frequency. Thus the frequency is proportional to the velocity. It also means that the phase shift curve is sampled fewer times per oscillation, giving an equivalent effect as reducing the PRF..

The limitations of Pw Doppler is the limited sampling rate, that allows only velocity measurement under a certain velocity, the Nykvist limit.

The Nykvist limit.

The Nykvist phenomenon (231) is an effect of the relation between the sampling frequency and the observed velocity. If you sample at a certain frequency, the direction of the motion becomes ambiguous, more frequent sampling will give the correct direction, less frequent sampling results in an apparent motion in the opposite direction. This can be observed with a stroboscopic light, for instance illuminating the flow of water


Cw Doppler, sampling the phase shift curve (Dopplwer frequency) once per pulse. The curve is very well reproduced.	Pw Doppler samples the curve with much lower sampling frequency (PRF), but still sufficient so the curve can be reproduced, both the value and direction of the velocity can be measured.	Pw Doppler where sampling frequency (PRF) is 4 × the Doppler frequency. The curve will still reproduce the troughs and peaks of the curve, and the information of the direction, and doesn't fit the alternate curve (same frequency, but out of phase (corresponding the the same velocity in the opposite direction.

Sampling at 2 × the Doppler frequency (i.e.) twice per oscillation, PRF = 2 × fd, the curve cannot be reproduced, i.e. the Doppler frequency cannot be measured, the samples fit both curves equally well, and the velocity direction is ambiguous.	- and the samples fit equally well the double Doppler frequency, i.e. twice the velocity.	Finally when PRF is < 2 × Fd, the sampling will fit other velocities as well, in this case 1.5 × velocity.

The phenomenon where velocities becomes ambiguous above Nykvist limit, is called aliasing.

It is often observed with old fashioned wagon wheels in old moves which often seem to revolve slowly backwards when the wagon moves forwards.

This is illustrated below as an example.

Constant rotation velocity, decreasing sampling frequency: The easiest is to show how reducing the sampling frequency affects the apparent motion. All circles rotate with the same rotation velocity clockwise. The sampling frequency is reduced from left to right. It can be seen that the red dots is at the same positions when they are seen to move.

a: 8:1 8 samples per rotation, the red point is seen in eight positions during the rotation.	b: 4:1 4 samples per rotation, the red point is seen to rotate just as fast, but is only seen in four positions	c: 2:1 2 samples per rotation, i.e. the sampling frequency is exactly half the rotation frequency. Here, the red dot is only seen in two positions, (but it is evident that it is in the same positions at the same time as in a and b). However, it is impossible to decide which way it is rotating. This is the Nykvist limit; sampling rate = 1/2 rotation rate.	d: 1.5:1 1.5 samples per rotation,or one sample per three quarter rotation, making it seem that the red dot is rotating counter clockwise. Again, the dot is in the same position at the same time as in a and b.
Constant sampling frequency, increasing rotation velocity The same principle applies when there is a fixed sampling frequency, but increasing rotational velocity. In the images below, the frames are seen to shift simultaneously, but the positions of the red dots are different due to the different rotational velocity.

a: 1:8 One rotation per 8 samples. The sampling catches the red dot in 8 positions during one rotation.	b: 1:4 Rotation velocity twice that i a; one rotation per four samples, the sampling catches the red dot only in four positions during one rotation.	c: 1:2 Rotation velocity four times a; one rotation per two samples, this catches the red dot in only two positions, giving directional ambiguity as above.	d: 1:1,5 Rotation velocity six times a; one rotation per 1,5 samples, or 3/4 rotation per sample, giving an apparent counter clockwise rotation.

Sampling from increasing depth will increase the time for the pulse returning, thus increasing the sampling interval and decrease the sampling frequency. The Nykvist limit thus decreases with depth. This means that pulsed Doppler has depth resolution, but this leads to a limit to the velocities that can be measured.

Frequency aliasing occurs at a Doppler shift that is equal to half of the PRF. f_D = ½ × PRF, i.e. two samples per wavelength, as described above.

f_Dmax= ½ × PRF
v_max = c × PRF / 4 f₀ cos()

Thus the maximum velocity (Nykvist limit) depends on the transmit frequecy, while the PRF depends on the depth. As the maximum PRF decreases with depth, so does the Nykvist limit. PRF = c / 2d. Thus:

v_max = c² / 8 d f₀ cos(

)

Depth	Maximum (Nykvist) velocity
Transmit frequency (f₀)	2 MHz	5 MHz	10 MHz
1 cm	1480 cm/s	590 cm/s	295 cm/s
5 cm	295 cm/s	120 cm/s	60 cm/s
10 cm	150 cm/s	60 cm/s	30 cm/s
15 cm	100 cm/s	40 cm/s	15 cm/s
20 cm	75 cm/s	30 cm/s	15 cm/s


Pulsed wave LVOT flow velocity curve, sampled at adequate PRF, corresponding to a Nykvist limit of ca 1.2 m/s.	The same LVOT flow velocity curve sampled at too low PRF, corresponding to a Nykvist limit of ca 0.6 m/s. Aliasing is evident. both positive and negative velocities are present.	Aorta flow velocity curve sampled at same PRF. By baseline adjustment, the limit for aliasing can be adjusted to 2× Nykvist, (but at the cost of total aliasing in the other direction.

If the velocities are much higher than the Nykvist, aliasing will occur at many multiples of the Doppler freqency:

Aliasing at 1/2, 1 and 2 × sampling frequency


Aortic insufficiency shown by cw Doppler. It van be seen that there are a fair distribution of velocities in the whole spectrum. However, There are far more velocities below 2 m/s. In this case, the low pass filter is only set to suppress tissue velocities. If the point is to get a clear visualisation of the maximal velocities in the jet, at 4 - 6 m/s, the filter should be set higher.	The same patient by pulsed Doppler of the LVOT. The outflow can be seen as a narrow band, within the velocity range, while the regurgitant jet has velocities far outside the Nykvist range, and there is total velocity ambiguity.

This means that both methods has limitations: pulsed Doppler has velocity ambiguity at high velocities, and continuous wave Doppler has depth or range ambiguity. Thus, for continuous Doppler the pulse length can be long, as there is no depth resolution, while in pulsed Doppler it has to be shorter in order to achieve a sufficient depth resolution.

High Pulse Repetition Frequency (HPRF)

A way around the problem, is to use high pulse repetition frequency pulsed Doppler. This means that one or more new pulses are sent out before the echo from the desired depth of the first is received. This will increase the pulse repetition frequency, and thus increase the Nykvist limit as the f_N = ½ * PRF. On the other hand it will be impossible to determine which pulse is the origin of the echo, and thus it will result in a partial depth ambiguity.

The principle of HPRF. Pulses are transmitted with three times the frequency that is necessary to allow the echo from the furthest depth to return. Thus, the echo of pulse 1 will return from level 3 at the same time as the echo of pulse 2 from level 2 and and of pulse 3 from level 1, and there is no way to determine whether a signal is from level 1, 2 or 3.

HPRF pulsed Doppler recording (right). with one sample volume in mid ventricle and one in the mitral ostium. The recording shows a systolic dynamic gradient (due to inotropic stimulation with dobutamine), as well as an ordinary mitral inflow curve. There is no way in the pulsed recording to determine which velocities that originate from which sample volume (except from á priori knowledge, of course, a dynamic gradient like this is usually mid ventricular, and the mitral inflow in the annulus is easily recognised).

Thus, HPRF can be uses to get higher velocity range, at the cost of semi-selectivity for depth. The differentiation of the different velocity curves will be dependent on recognition from prior knowledge.

Aliasing is no problem in pulsed tissue Doppler, as tissue velocities are far below the Nykvist limit. However, in colour tissue Doppler, harmonic imaging is halving the effective frequency, and leads to aliasing as shown below.

Velocity filtering

The Doppler frequency diagram. The signal can be filtered. For Doppler flow, a high pass filter (low velocity reject) is applied to suppress stationary echoes (clutter) as well as low amplitude tissue echoes. The filter is variable, and thus can be applied to select for very high velocities in insufficiency jets. A low pass filter (high velocity reject) can be applied to suppress noise above the velocity range.

Typically, tissue has high amplitude and low velocity, while blood has low amplitude, but a high velocity. As B-mode is a pure amplitude imaging, this means that tissue is bright, blood is black.


Amplitude imaging (B-mode). Tissue echoes have a high amplitude, blood a low amplitude (due to low reflexivity). Thus tissue is visualised , while the blood is not visible in the present gain setting.	As seen from the B-mode image to the left, the tissue is not stationary, but the velocities are low, compared to blood.

Too see blood flow velocities, it is possible to increase gain, but that will also increase the low velocity signals from the tissue to saturation. They are generally considered clutter nois, when dealing with blood flow, although it is not true clutter in the reverberation sense.	It is possible to filter the low velocities by a "high pass filter", that allows high velocities to pass, while removing low velocity signals independent of amplitude. This will remove both tissue signals and reverberation noise. The low velocities around the baseline have been removed, the width of the filter is indicated by the green band to the left. This is also called "clutter filter" or "low velocity reject".

Bandwidth

As the bandwidth is a function of the pulse length as described in the ultrasound section, bandwith is a function of the pulse length. Spectral analysis will yield a spectrum that minimum is as wide as the bandwidth.


As described above, a pulse has a certein bandwidth, describing the frequency content of the pulse. In spectral analysis, this will give a spectrum of a certain width, corresponding to the velocity distribution of flow velocities. In phase analysis, this will correspont to a certain distribution of phase angles as illustrated. Autocorrelation, however, will only result in the average phase angle.	In the case of stationary noise (clutter) as f.i. reverberations, the autocorrelation will result in an average phase angle that is in between the signal and the noise. The clutter noise will have to be removed by a low velocity filter in order to avoid severe underestimation of flow velocities.

Ideally, the pulse length in Doppler should be long, in order to increase velocity resolution. However, this will reduce the spatial (axial) resolution and the PRF.

Thus, if the dispersion of velocities is larger than the bandwidth, as in flow measurements, this is the most important. On the other hand, if there is little dispersion of velocities, as in tissue velocities, the width of the spectrum reflects the bandwidth.

But the insonation angle also has an influence, not only in the velocity measurement according to the Doppler equation. but also in the bandwidth as shown below.

As can be seen, the direction of the motion of the scatterer in relation to the direction of the pulse, may influence the number of oscillations that are actually used for measurement. Thus, a high insonation angle is equivalent to a virtual shortening of the pulse length, and results in a wider bandwidth (spectrum).

Vascular ultrasound, illustrating how the beam to flow angle affects the spectral width, even when angle correction is applied, in line with the above discussion. This spectral broadening also affect the values of the peak velocities. Flow direction is evident in vascular ultrasound, being in line with the vessel, not so evident in intracardiac flow. Image courtesy of Ingvild Kinn Ekroll.

Finally, stationary reverberations, creating artificially stationary echoes will result in widening of the spectrum in tissue Doppler. In flow, this will basically be removed by the high pass filter.

Colour Doppler mode (CFM)

Basically, colour Doppler is pulsed Doppler. The method will give the velocity at a certain depth, depending on the range gating as in pulsed Doppler. By gating multiple sampling times from the same pulse package in post processing, the Doppler shift can be measured at multiple depths along the line. A pulse package is trensmitted, but instead of only one range (time) gate, there are multiple gating of the return pulse (the opposite of HPRF). This results in there being no depth ambiguity (except in reverberation artefacts). This means that the method is similar to B-mode. In fact, colour Doppler can be seen as a B-mode, where the phase (or frequency) shift is analysed instead of the amplitude, stored as numerical values in each pixel (as amplitude is in B-mode), but displayed as colour instead of brightness.It also means that the PRF is limited by the maximum depth of the colour sector, i.e. the farthest range sample, and the Nykvist limit for maximum velocity is determined by that.

Secondly, the method is used for building a sector, just as in B-mode, where the next pulse is sent out with a small deviation, building a new line in the sector, as in B-mode. However, in order to use phase analysis, more than one pulse (at least two) must be sent along each line, before the next line can be sent out. This places a limit on the maximum frame rate, which then is given by the PRF as well as the number of pulses in a package.

The time between packages can be used for sampling B-mode data for a B-mode image in a composite image. In the Doppler signal, tissue echoes is removed by clutter filtering, but an amplitude filtering may also be applied.


In colour Doppler one pulse package is sent out as in Pw Doppler, but the return signal is sampled multiple times as in B-mode. Since there is only one transmit pulse (package) at a time, there is no range ambiguity, each return sample corresponds to one specific deph, as in B-mode..	Relation between PRF and frame rate. The diagram illustrates a scatterer moving in a Doppler field. In order to do phase analysis, at least two pulses (a pulse package) need to be sent out along one line, the time between them corresponding to the PRF, which again is limited by the maximum depth of the colour sector. When the Doppler shifts have been sampled along one line by a pulse package, a new pulse package is sent out along the neighboring line, building a sector image analogous to B-mode. Thus, the position of the scatterer can be seen to be sampled only with the frame rate, which is lower than the PRF, depending on the depth, width and resolution of the colour sector.	CFM sector superposed on a B-mode sector. By reducing sector size, line density and sampling frequency, the CFM image can achieve an acceptable frame rate. This is feasible because the region of interest for the flow is usually only a part of the ROI for The B-mode, flow being intracavitary as shown below.

In colour Doppler, there is not spectral analysis. As seen by the colour display, there is only one velocity value per pixel. The phase analysis of the relative positions of all four points is done by autocorrelation, a quick (and dirty?) method that allows online computation. This gives the mean Doppler frequency per pulse package per pixel.

CFM sector superposed on a B-mode sector. Blue: Negative velocities (away from the probe), Red: Positive velocites. The display is semi quantitative, but the underlying data are quantitative. Both B-mode and colour Doppler is acquired at the same time, but with different pulses, beamfoming and line density. The sector with colour flow is seen to be smaller than the B-mode sector. The image displays the direction, extent and timing of the jets.

In principle, two pulses are sufficient for phase analysis with perfect signals. However, more than two pulses can be used in order to make the analysis more robust, in the autocorrelation method. This results in better accuracy (reliability) of the velocity estimate. This, however increases the duration of each package (as the time between two pulses is 1/PRF, a package of N pulses will have a duration of N-1/PRF), and thus it will affect frame rate. The PRF can be increased by reducing depth, reducing line density in the Doppler window, or reducing sector width.

A theoretical frame rate of 1 KHz will make the use of packets unnecessary (as then PRF = FR, and phase analysis can be done from one puls to the next, with the same Nykvist frequency). This is technically feasible (272), and has been implemented in a novel application; Ultra high frame rate tissue Doppler (UFR-TDI) (215 ,268).

Also, the possibility to display the full velocity information in each pixel is limited. In order to display multiple velocities in real time over a sector, the numerical values are usually displayed only semi quantitatively as color. Power Doppler shows the amplitude of the Doppler shifted signal, i.e. the blood flow.

Power Doppler image of the renal circulation. The amplitude is a function of the number of scatterers, i.e. the number of blood cells with a Doppler shift. This is shown as the brightness (hue) of the signal. In addition, direction of flow can be imaged by different colours (red - positive flow - towards probe, blue - negative colours - away from probe), and still the brightness may show the amplitude.

Colour flow showing a large mitral regurgitation. Velocities away from the probe is shown in blue (converting to red where there is aliasing), towards the probe is red. In this image, the green colour is used to show the spread (variance) of velocities. This will also reflect areas of high velocities (high variance due to aliasing).

2D colour flow gives mainly information on the direction of velocities, as well as colour M-mode giving the direction - timing information. However, the information is numerical, and can be extracted as is done in colour tissue Doppler, but this gives far less accurate values than pulsed and cw Doppler, as well as a reduced frame rate.

Recording from a patient with apical hypertrophic cardiomyopathy. Ejection can be seen in blue, and there is a delayed, separate ejection from the apex due to delayed relaxation. There is an ordinary mitral inflow (red), but no filling of the apex in the early phase (E-wave), while the late phase (A-wave) can be seen to fill the apex. Left, a combined image in HPRF and colour M-mode. The PRF is adjusted to place two samples at thr mitral annulus and in the mid ventricle just at the outlet of the apex. The mitral filling is shown by the green arrows, and the late filling of the apex is marked by the blue arrow. In addition, theere is a dynamic mid ventricular gradient shown by the red arrow, with aliasing in the ejection signal in colur Doppler. The delayed ejection from the apex is marked by the yellow arrow (the case is described in (87). The utility of the different methods is evident: HPRF (or cw Doppler) for timing and velocity measurement, but with depth ambiguity, colour M-mode for timing and location of the different jets, direction being displayed by the colour.

The phase analysis is often done by the process known as autocorrelation. This will result in a values that does not reflect the spectrum, but only mean values in the spectrum. But if there is clutter in the region (stationary echoes), this will be incorporated in the mean, resulting ion lower values. In Doppler flow, this can be filered by the high pass filter, and thus will represent a small problem. In tissue Doppler, this may be a more significant problem, as the velocities are only about 1/10 of the flow values, and thus clutter may be more difficult to separate from true velocities. Thus, a substantial amunt of clutter may reduce autocorrelation values for tissue Doppler more than pulsed Doppler as discussed below. In addition, it is customary to analyse the tissue Doppler values in native, rather than harmonic imaging, due to the Nykvist limitation. Thus, there is a greater amount of clutter than if harmonic imaging had been used, as shown in B-mode images.

For optimal colour flow, it is important to realise that there may, in some scanners, be an inverse relation between the gain of colour Doppler and B-mode. (In some scanners it is possible to adjust the priority, or to adjust the gain settings separately). This, however, is an acquisition finction, and not image adjustment, and thus cannot be compensated afterwards. This is illustrated below:

Effect on B-mode gain on colour Doppler imaging. Left pulmonary venous flow by pwDoppler, showing a systolic flow component, although low velocities. Middle, colour M-mode of the same patient. Only the diastolic flow component can be seen. Right, reducing B-mode gain increases the gain of colour flow, and the systolic pulmonary venous flow can be seen.

Relation between flow velocity and flow

Doppler gives flow as a velocity. This means the velocity shows how rapidly the blood volume moves along the path, the distance per time v = d/t and is given in m/s. The velocity says nothing about the amount of blood, however. Flow is the volume rate: volume per time Q = V/t and is usually given in litres per minute. But given constant orifice area, any changes in velocity will be proportional to the change in blood volume flow, showing that there is a fundamental relation between cross sectional area of the flow, and the velocity:

Relation between velocity and flow with constant flow velocity. In this case, the velocity is distance / time v = d / t. During this time interval the distance times cross sectional area defines a volume V = A × d, which is the volume circumscribed by the motion with the velocity v. Flow (volume rate, volume per time) during the same interval t is Q = V / t, so Q = A × d / t = A × v.

Variable flow velocity - pulsatile flow

This, however, holds only for constant flow velocity. Blood flow is pulsatile, but the fundamental equations of motion still hold:

With varying velocity, velocity is the derivative of distance per time, and distance is the integral of the velocity. Integrating the velocity over a certain time, then defines the length of a cylinder travelling with that varying distance. Multipålyong by area gives the vloume of a cylinder, that equals the volume flow during that time.

This relation holds when veloctiy is varable, but cyclic, i.e. pulsatile flow.

In the heart this can be used to calculate the stroke volume (232):

Stroke volume by Doppler. The cross sectional area is given by the diameter, under the assumption of a circular orifice. Tracing the velocity curve over one heart cycle, gives the integral of the velocity by the area under the curve (VTI). This represents the stroke distance, i.e. the distance traveled by something (blood) travelling by the varying velocity given by the Doppler curve. The stroke volume is then given by the area × the velocity integral.

Variable area - flow across stenoses:

In a continuous channel, flow is contiguous, and must be the same across every cross section, i.e. independent of cross sectional area:

As the area A₁ is larger than A₂, in order to push the same amount of blood through A₂, the velocity v₂ must be higher than v₁. As the flow is the same, and given by A×v for continuous, and A×VTI for pulsatile flow, the ratio of velocities / velocity time integrals is the inverse of the ratio of areas. This is the continuity equation.

Using the continuity equation, as the LVOT diameter (and area) is known, tracing the VTI of the LVOT flow (pw Doppler to do it in the correct level) as well as the VTI through the valve (cw Doppler). The VTI equals the stroke length, and the stroke length times the atra, equals the stroke volume. As the stroke volume is constant, the two cylinders have equal volume, and thus, the valve stenosis area (AVA) can be calculated by AVA = LVOT area × VTI_LVOT / VTI_AO

This demonstrates that as contiguous flow needs to be constant, flow velocity will vary with the cross sectional area, and thus will not be representative of flow, unless area is taken into account.

The continuity equation for aortic valve area has been validated against the Gorlin formula (233):

Relation between flow velocity and pressure:

Fundamentally, both velocity and pressure represents energy. The potential energy in a fluid under pressure, is given by E = P × V, while the kinetic energy is E = ½ m v². But this means that when velocity increases, this kinetic energy has to be recruited from somewhere, which is the pressure energy. Thus, as velocity increases, pressure has to drop:

As velocity increases for the same volume that passes point 1, also must pass point 2, the increase in kinetic energy pressure is recruited from the pressure energy. Thus, there is a pressure drop from 1 to 2. The full equation for the acceleration of the fluid is given in the Bernoully equation. However, it has been shown that both the flow acceleration part and the friction parts are so much smaller than the first part (which is the basic energy difference), and may be ignored. Thus, the modified Bernoully equation relates pressure differences to the square of velocity differences. And if v₂ is much smaller than v₁, the modified equation may be simplified even more. And of course, the simplest form, is still an acceptable approximation if P₂ is much lower than P₁.

The simplified Bernoully equation has been shown to be valid for pressure gradients across mitral stenosis (234, 235), aortic stenosis (236), and estimation of RV pressure from tricuspid regurgitation (237).

Pressure recovery

As discussed above, as flow converges towards a stenosis, there is little friction, meaning that there is laminar flow towards the stenosis. When flow has passed the stenosis, and into a receiving chamber where there is larger area, the velocity will decrease again. However, this may have different consequences. If there is perfectly laminar flow after the stenosis, the friction element is still so small, that the kinetic energy reverts to pressure: there is pressure recovery, and the pressure rises to the pre stenotic level. Doppler measurement will still measure the maximum pressure drop, and so will a manometer placed at the narrow part, but manometers before and after the stenosis will not register pressure drop.

On the other hand, if the flow is not perfectly laminar, there will be turbulence after the stenosis, resulting in frictional energy loss, and the velocity will decrease without restoring pressure energy, i.e. the energy is lost, and there is not pressure increase after the stenosis. In that case, there the Doppler gradient may be a true measure of pressure drop.

Full, partial and zero pressure recovery. The pressure drop corresponding to the velocity increase, is P_max, the maximum pressure drop, given by P₁ - P₂. The net pressure drop through the stenosis, P_net, however, is given by P₁ - P₃. Cw Doppler measures P_max, (and so will a manometer placed directly into the stenosis, and may thus over estimate the effect of the stenosis.

Left is perfectly laminar flow through the stenosis. In this case, the post stenotic velocity decelerates without energy loss, and the kinetic energy is converted back into pressure again. Here, there is no net pressure drop through the stenosis. Driving pressure at P₁ does not have to be increased to maintain pressure at P₃, and the pressure drop at P₂ is temporary. It must be remarked, however, that pressure recovery cannot be more than the initial pressure.

In the middle is partial pressure recovery. Some of the pressure energy converted to kinetic energy through the stenosis is lost when the flow velocity decelerates after the stenosis, in the form of turbulence resulting in friction. But some of the energy is recovered to pressure energy again. Thus, there is a net gradient over the stenosis, but this is less than the maximum gradient. The maximum gradient by Doppler will over estimate the net gradient.
The red line represents the situation if the driving pressure is constant, thus the post stenotic pressure drops. The blue line represent the situation if P₃ is regulated (as in the aorta). Then P1 has to be increased corresponding to P_net in order to maintain P3. This represents the extrta work or load induced by the stenosis.

Right, there is total energy loss through the stenosis, all kinetic energy due to the velocity increase through the stenosis is lost in turbulence and friction. Thus, P_max = P_net and the maximum gradient is a measure of increased work (load) in order to maintain P₃.

As discussed above, if pressure measured across an aortastenosis is higher than normal intraventricular pressure, there has to be a net gradient, as the maximum pressure drop has to be positive.

Tissue Doppler

In tissue Doppler, the high pass filter can be removed, or at least partially, to allow the low velocities from the tissue. It can be maintained at low levels to suppress absolutely stationary echoes (clutter). The blood signal can be removed both by reducing the gain, and by applying a low pas filter.

As shown above, the tissue velocities are present in the Doppler spectrum, and with far higher amplitude than the blood flow signals. In blood flow Doppler, the tissue signals are usually removed by the clutter filter, in order to get cleaner blood flow signals.

Spectral Doppler from the LVOT. Both tissue velocities and blood flow velocities can be seen, and by reducing gain below saturation of the tissue signal, the tissue velocities can be seen as distinct, and typical curves, showing both S', e' and a' peaks. The image demonstrates both that flow velocities are aboput ten times tissue velocities, but also that the Blood flow Dopple rhas a much lower amplitude.

The Doppler principle can be used both for blood flow and Tissue velocities. Tissue Doppler was first decribed in 1989 (53). It is simply a question of different filtering of the Doppler signals. The main principle is that blood has high velocity (Typically above 50 cm/s, although also velocities down to zero), but with low density, resulting in low intensity (amplitude) of reflected signals. Tissue has high density, resulting in high intensity signals, but low velocity (typically below 20 cm/s). The difference in the applications used for the two sets of signals is mainly differences in filtering, applying a high pass filter in Doppler flow, and low pass filter in tissue Doppler (Although the latter is not absolutely necessary, as shown).

Spectral tissue Doppler

In Tissue Doppler , only the Pw mode is useful, as velocities are so low, that cw Doppler doesn't add anything useful, while the location of the sampåle volume is always important.

It is again important to realise that pulsed tissue Doppler has a high sampling rate (up to 1000), but a low temporal resolusion (effective frame rate usually below 100 FPS) due to the Fourier analysis over a long window as explained above.


The diagram to the left shows the placement of flow and tissue signals on this intensity (amplitude) / velocity diagram. Velocity given as the height ogf the bars, intensity shown both by the placement on the x axis, as well as the darkness of the bars, black being the highest intensity. The flow signals are low intensity but mostly high velocity, while the tissue is exclusively low velocity, high intensity. The heart valves, however, are solid structures which moves with the velocity of the passing blood, resulting in high velocity signals. Intensity may be seen to be higher. A typical flow curve from the LVOT ventricular outflow tract is shown to the left, with the valve click.

Application of a high pass filter (low velocity reject) shown schematically to the left and in practice applied to the LVOT flow curve to the right. Velocities lower than the limits of the green bar (showing the range of the filter) are removed seen in the dark zone in the middle of the spectrum. The setting rejects velocities below 15 cm/s. Wall velocities are generally lower, and is filtered.

The filter is adjustable, and is here reduced below 10 cm/s. This results in high intensity signals becoming visible, especially in early diastole. This are tissue signals from the LVOT.

Further reduction results in high intensity tissue signals around the baseline. The signal is difficult to analyse, as it has so high amplitude that the display is saturated.

Fully decreasing the filter, and decreasing the gain, (shown as all signals being illustrated in lighter colour, but with the same relative placement on the x axis), discloses the tissue velocity curve, while the flow signal, having a much lower amplitude, is much less visible.

Reducing the scale, increases the resolution of the tissue velocities, that are still taken with ordinary Doppler.

All modern ultrasound machines today has separate applications for tissue Doppler which optimises the signal for this purpose, among other things by applying a low pass filter that removes most of the flow velocities. This results in a cleaner signal.

Measurement of peak values in relation to the Doppler spectrum

The width of the spectrum in Doppler flow is mainly determined by the dispersion of velocities. The middle of the spectrum, is the average of the main velocities.

However, the main use of pulsed wave tissue Doppler is for measuring annulus velocities, and the annulus is stiff, with little probability of dispersion of velocities. Also, in pulsed tissue Doppler, the insonation angle is small. Despite this, the spectrum has a certain width, indicating a spectrum of velocities:

Spectrum width in tissue Doppler. Image courtesy of H Dalen.

Thus, the main determinant of the width of the spectrum is determined by the bandwidth. The bandwith is determined by the pulse length and pulse frequency, and represents the frequency spectrum in the received signal . As this frequency is due to the frequency distribution in the transmitted signal, as well as the uncertainty in frequency measurement, the frequency distribution is statistical, and more or less normally distributed around the mean frequency (or velocity). In addition, it is distorted by non-linear propagation, adding frequencies to the return signal.

Ideally, the most representative value of the spectrum is the modal velocity (the velocity in the middle of the spectrum), not the maximal value (at the top of the spectrum). This will also be the values that are most similar to the tissue Doppler values obtained by autocorrelation (colour tissue Doppler) as shown below.

Recordings from basal septal mitral ring in a subject without substantial clutter. Spectral Doppler shows the dispersion of velocities, although this is probably an effect of bandwidth. The colour Doppler recording is superposed and aligned with both vertical and horizontal scale. In this instance can be seen to give values close to the middle of the spectrum (modal velocity).

Spectral Doppler reconstructed from IQ data. Candidates for measuring peak systolic velocity by the PW tissue Doppler spectrum. RED circle: peak of the spectrum at normal gain, GREEN circle: upper edge of the strongest part (the part visualised at minimal gain), BLUE circle: middle of the strongest part. MAGENTA circle and line: autocorrelation. As seen, imn this example the autocorrelation corresponds to the middle of the spectrum. (Figure courtesy of Svein Arne Aase

We tested this hypothesis in a preliminary study (240), using spectral Doppler reconstructed from IQ data.

For a reference method, Peak slope of systolic M-mode from IQ data in the same time point was chosen:

Reference method. A: pw Doppler from the mitral ring (reconstructed from RF data). Peak velocity of the ring displacement can be identified. B: This corresponds to the maximal slope of the M-mode line at the same time point. C: The M-mode in the same time window from the RF data. This gives a far better resolution in space and slope. D: In the RF M-mode the steepest sloe was identified automatically. This will be a reference for the maximal velocity. (Figure courtesy of Svein Arne Aase

As this figure shows, the peak spectrum results in a substantial overestimation. reducing the gain improves the over estimation, while the modal velocity is closest to the reference. Autocorrelation on the other hand results in significant under estimation, due to the presence of clutter. Only four subjects showed almost total correspondence between autocorrelation and modal velocity from spectral doppler. (Figure courtesy of Svein Arne Aase

It is evident that the modal velocity is closest to the "true" velocity, and thus if peak values are used, they should be obtained and analysed by the lowest readable gain setting.

The effect of gain on spectral Doppler

Historically the peak value (at the top of the spectrum), has been used in pulsed Doppler. Thus, most of the differences reported between pw Tissue Doppler (241) and colour tissue Doppler (16) are due to the width of the spectrum. But if so, this would give a good correlation between methods, and a more or less constant offset (16, 242). On the other hand, filtering of the colour tissue Doppler reduces peak values, and will also increase the difference between the methods (241). Autocorrelation with high filtering or low frame rate will thus underestimate the true mean value.

However, the width of the spectrum is sensitive to gain settings. As the frequencies are normally distributed around the mean, this means that the intensity in the periphery of the band is lowest, and will disappear earlier when gain is reduced. Increased gain setting increases the peak values (241) as illustrated below:

In this case, differences in gain leads to a difference of 3 cm/s in systolic peak values, and 3.5 cm/s in early diastolic peak values.

In perfect image quality, modal velocity should be equal to autocorrelation, but in the case there is clutter, autocorrelation would not give similar values, as clutter would be incorporated into the mean. In the study above, this was the case with most subjectys, resulting in a significant difference between modal velocity from spectral Doppler and autocorrelation. This is further discussed below.

Colour Tissue Doppler

The basic principles of colour tissue Doppler are the same as for colour flow mode (239). The difference is the same as in spectral Doppler flow versus colour Doppler flow, except for the differences in filtering as shown above. colour However, the region of interest is the same as in B-mode, being the myocardium. Thus the solution of a small sector within the B-mode sector is unfeasible. However, as velocities are measured only along the ultrasound beams, and cavity signals are filtered by low gain / low pass filter, the line density need not be high. In addition, as the data are for numerical analysis, not imaging, artifacts from MLA are unimportant. Thus, high frame rate in a full B-mode sector is achieved with a very low line density, and a higher MLA (typically 4). Thus the B-mode and colour Doppler images are displayed superposed, but the acquisition is interleaved, recording a multiple of colour Doppler images between each B-mode frame. (For instance 16 lines acquired by 4 MLA in colour Doppler interleaved with one B-mode image acquired with 64 lines at 2MLA for every fourth Doppler image will result in a Doppler frame rate of 160 for a B-mode frame rate of 40).

Both velocity and strain rate information can be displayed on the B-mode image, as coour representations of the numerical pixel values, just as in colour flow. However, as seen below, in this case the main purpose is not display location of jets, as most motion and deformation is fairly more uniform. In addition, shifts are too quick to visualise entirely, so the visual colour cine display is less useful.

Velocity (left) and strain rate (right) imaging of the same (normal) left ventricle. The colour sector is usually set equal to the B-mode sector. Velocity is red in systole when all parts of the heart muscle moves toward the probe (apex) and blue in diastole. Strain The changes are too quick to observe entirely, to make full use of the information the image has to be stopped and scrolled.

Thus, in colour tissue Doppler, the main function is to get data for post processing. The advantage over pulsed Doppler, is the near simultaneity of the data over the sector, being important in comparing regional motion from different segments of the wall. In colour flow, simultaneity is less important, and so quantitative information is rather acquired by pulsed or cw Doppler, giving higher temporal resolution.

Thus, tissue velocities can be extracted to numerical traces, to enable measurements of

peak velocities
integrated velocity- motion
velocity gradients - strain rate
integrated strain rate - strain

The relation between motion (velocity and displacement) and deformation (strain and strain rate) is treated here.

Septal strain and strain rate (right) from (nearly) the whole septum, and basal septal velocity and displacement (left). As the apex is (nearly) stationary, the basal velocity and displacement is a motion inscribing the whole of the shortening of the wall, displacement is the time integral of the velocity curve, both are motion measures. The heart cycle shows ventricular shortening and annular motion towards the apex during systole, ventricular elongation and annular motion away from apex during the two diastolic phases. The deformation curves from of the whole wall is very similar to the inverted motion curves from the base, as strain rate and strain are the spatial derivatives of velocity and motion /velocity and shortening per (length unit) along the wall.

The information coded in the colour images, is fundamentally numerical for all varieties of colour Doppler. Thus, the velocity time traces can be extracted fom any point in the image as shown below. However, both the primary velocity data, as well as the calculated date can be displayed as parametric (colour) images images, of which the curved M-mode (CAMM) (254) is the most useful so far, mainly for assessment of timing.

Longitudinal velocity gradient (strain rate)

The concept of velocity gradient was introduced by Fleming et al (20), defined as the slope of the linear regression of the myocardial velocities along the M-mode line across the myocardial wall. If velocities are linearly distributed through the wall, this is equal to the difference in endocardial and epicardial velocities divided by the instantaneous wall thickness (W):

The definition of transmural velocity gradient was extended by Uematsu (21), by applying the velocity gradient to wall thickening velocity in any direction in the 2D cross sectional image, by means of angle correction of the velocities.

As the apex is stationary, while the base moves, the displacement and velocity has to increase from the apex to base as shown below.


As the apex is stationary, while the base moves toward the apex in systole, away from the apex in diastole, the ventricle has to show differential motion, between zero at the apex and maximum at the base.	As motion decreases from apex to base, velocities has to as well. This is seen very well in this plot of pwTissue Doppler recordings showing decreasing velocities toward apex. Thus, there is a velocity gradient from apex to base

The simultaneous measurement of velocities by colour Doppler in the whole sector, enables the measurement of instantaneous velocity differences.

At the NTNU, Andreas heimdal was working with deformation imaging, while I was working with long axis left ventricular function at the same time. This led to me suggesting to apply the velocity gradients to the longitudinal shortening, which are greater in magnitude, making the rough method more robust, as well as making all segments of the ventricle available for analysis, and resulted in the first publication on strain rate imaging (22).



The strain rate can be described by the instantaneous velocity gradient, in this case between two material points, but divided by the instantaneous distance between them. In this description, it is the relation to the instantaneous length, that is the clue to the Eulerian reference.	Strain rate is calculated as the velocity gradient between two spatial points. As there is deformation, new material points will move into the two spatial points at each point in time. Thus, the strain that results from integrating the velocity gradient, is the Eulerian strain.

The strain rate was calculated as the velocity difference between two spatial points, divided by the distance between them, but this is equivalent to the velocity gradient, and thus to Eulerian strain rate.

Tracking the two points of the object as material points, the result will be the velocity gradient. In tissue Doppler, however, it is customary to measure at fixed points in space. This means that

x is constant, and not the instantaneous length of the segment between to moving points. In addition, the material points will move through the measurement points, so the velocities will represent velocities of the spatial, not material points. L (which is shortening) and

x (which is constant) are not equal, except at one point in time when

x equals L, at that point v(x) = v2 and v(x+

x) = v1. However, Usually, however, L will differ from x, for most frames and objects, and the velocities will hence differ too. Under the assumption that the strain is equally distributed over the length of the object (spatially constant), however, SR will still be equal to the velocity gradient at all points in time, i.e the value of the two ratios will be the same. Strain being spatially constant means that the velocity increases linearly along the length as shown in the diagram:

In this case, it is evident that in the changing L, the velocities change simultaneously, keeping the ratio between the differences and the instantaneous length constant (0 the slope). This is also the case for the ratio between the difference in velocities, v(x) - v(x + x) and x. As v1 and v2 are the velocities of the end points of L, the ratios SR and VG will be the same, and thus the expressions are equivalent: SR = VG and the strain rate by tissue Doppler (SR) equals Eulerian strain rate.

Is there a gradient of strain and strain rate from base to apex as well?

The velocity gradient from base of the LV to the apex looks fairly linear:

Peak systolic velocity plot through space, from the septal base to the left through the apex in the middle to the lateral base to the right. The velocities seem to be distributed along fairly straight lines, i.e. there seems to be a fairly constant velocity gradient.

Thus, while peak velocities decrease, peak strain rate is more or less constant from base to apex if the gradient is constant.

An infarct is visible as a reduction of the slope, and the concomitant hyperkinesia in neighboring segments due to reduction in local load as an increase in the slope.

Anterior infarct, seen in the V-plot from a 2-chamber image as hypokinesia in the apical two segments, with concomitant hyperkinesia in the basal regment. There is substantial clutter noise in the inferior wall.

Strain rate and strain assessed by offset between velocity curves

Strain rate and strain can be visually assessed by the offset between the curves, when the velocity curves are obtained from points with a known (and equal) distance.

Top left: Velocity curves from four different points of the septum. The image shows the decreasing velocities from base to apex. The distances between the curves show the strain rate of each space between the measurement points (segments). Top right: the resulting strain rate curves from the segments between two and two of the velocity ROIs displayed. Bottom left: Displacement curves from the same four different points of the septum, obtained by integration of the velocity curves. The image shows decreasing displacement from base to apex. The distances between the curves show the strain of each space between the measurement points (segments). The resulting strain curves from the segments between two and two of the velocity ROIs shown to the right.

If the curves are taken from the segment borders, this is a representation of the segmental strain rate and strain. Thus, it is evident that the strain rate and strain can be visualised (qualitatively) by the spacing of the velocity and displacement curves, even without doing the derivation.

An infarct will show up as decreased distance between the velocity curves.

Top: the same velocity and strain rate curves as in the previous picture, showing even distribution of the distances between velocity curves, and equal strain rate in all segments. Bottom, a patient with a small infarct in the apical segment, where the distance between the two apical velocity curves is lo, and so is the strain rate curve from the segment beweeen them.

Strain rate by linear regression of velocities

Looking at the V-plot again, it is evident that there is a substantial variability in velocity estiamates from pixel to pixel. This, of course, will result in a greater variability of strain rate measurements, as the variability will be the sum of the relative variabilities of the single measures, while the strain rate is the difference, resulting in a substantially worse signal-to-noise ratio.

V-plot, showing the real variability from pixel to pixel of velocities.


Velocity measures with some amount of noise.	Unsmoothed strain rate curves from the same loop. The increase in noise is evident.

Instead of measuring just the velocities at the ends of the offset distance; or respectively, the velocity gradient / strain rate can be calculated as the slope of the regression line of all velocities along the offset distance as described originally (14). With perfect data, the values will be identical, both formulas defining the slope. With imperfect data, this method will tend to make the method less sensitive to errors in velocity measurements, as the value is an average of more measurements.

Strain rate calculated over an offset (strain length) of 12 mm (L). "True" velocities at the end points are v1 = 0 and v2 = 1.2 cm s^-1 giving a strain rate of -1.0 s^-1 (blue squares), the strain rate is actually the
slope of the line between the points, being equal to (v2 - v1)/L (blue line). Due to random variability of the measurements, the measured values deviate from the slope. Here velocities are sampled for each 0.5 mm along the
strain length (red points), and are seen to be dispersed around the true strain rate line. The regression line through the points (red line) is fairly close to the true strain rate line, and results in a strain rate measurement
of -1.14 s^-1. This makes the measurement far less vulnerable to measurement variability than simply measuring the two velocities at the end of the strain length (points in the green open squares), and compute
SR = (v2 - v1)/L shown by the green line, yielding a strain rate of -1.63 s^-1.

Curved anatomical M-mode

This method, developed by Lars Åke Brodin and Bjørn Olstad shows the whole time sequence in one wall at a time. (18). By this method, a line is drawn in the wall, and tissue velocity data are sampled for the whole time interval (e.g. one heart cycle) and displayed in colour along a line in a time plot, as shown below. This has the advantage of displaying the whole sequence in a still picture, giving a temporal resolution like the frame rate of the 2D tissue Doppler.

Velocity and strain rate imaging of the same (normal) left ventricle. The colour sector can bee seen to be equal to the B-mode sector.Velocity is red in systole when all parts of the heart muscle moves toward the probe (apex) and blue in diastole. The changes are too quick to observe entirely, to make full use of the information the image has to be stopped and scrolled.

Curved anatomical M-mode (CAMM). A line is drawn from apex to base, and velocity data over time are sampled along the line and displayed in colour along a straight line. The numbers on the curve and the M-mode are included for reference and corresponds to the numbers on the B-mode image. This example shows the septum from the apex to base along one axis, and one heart cycle along the other, in a two - dimensional space - time plot. S: systole, E: early relaxation, A: atrail contraction.

Comparison of septal velocities (left) and strain rates (right), in traces (top) and curved M-modes (bottom). While the numerical traces display the quantitative values, in one point only for each curve, but for the whole cycle, the colour M-modes shows the semi quantitative display from the whole wall simultaneously, enabling direct comparison of the timing of events in different parts of the wall.

The CAMM is especially useful in strain rate, as the phases are better separated between different parts of the wall than in velocities, due to the elimination of the tethering effect. CAMM scan be extended to the whole sector as shown below:

Curved M-mode showing the full M-mode from basal septum through the apex to the basal lateral wall. The pre ejection shortening is shown to occur before MVC, systolic shortening is fairly homogeneous alont the whole wall, and IVC with apical lengthening and basal shortening is seen. In diastole, the propagation of the elongation waves both in early filling phase and during atrial systole, which also shows a propagation from base to apex, but with a higher propagation velocity. In addition, the elongation waves can be seen to either cross or return from the apex towards the base, but far weaker. This can also be seen above, as the basal strain rate are double peaked.

Reverberations (clutter) in tissue Doppler

In some cases, the mean velocity may be very far from the "true" modal velocity:

In this case, the spectral Doppler is "smeared out, all the way down to the baseline. The mean of all frequencies is shown on the spectrum in black. It is far from the peak values. To the right is the values from autocorrelation, which are similar to the mean values.

Reverberations may not be entirely stationary. It the reflecting surface that gives rise to the reverberation moves, the reverberation bands will move also, as seen in the simulations above, as well as the real acquisition below

Normal tissue Doppler curve from the mitral ring. Peak systolic velocity around 8 cm/s. However, a band with approximately the same shape, but systolic amplitudes of around 2 m/s van be seen as well, probaby a reverberation from the apical part.

Reverberations are often nearly stationary echoes, meaning that the echoes will incorporate zero velocities (clutter). Most of the reverberation echoes are in the fundamental imaging frequency. However, harmonic imaging halves the frequency, and thus the Nykvist limit. This means that there will be aliasing at half the velocity in harmonic imaging, compared to fundamental. And this is within the range of tissue velocities. Thus harmonic imaging is unfeasible in tissue Doppler, and the harmonic acquisition makes the method more vulnerable to reverberations than B-mode, as explained below.

Harmonic tissue Doppler

Harmonic imaging in tissue Doppler leads to aliasing, as seen by this colour M-mode. However, Strain rate imaging, using the velocity differences, will neutralise this, as usually both velocities in the equation (V1 - V2)/L are aliased, and thus the difference remains the same. So in strain rate imaging, aliasing is effectively unwrapped, as shown previously (167).


Colour M-mode (CAMM) of tissue velocities in fundamental (above) and harmonic (below) imaging. Slight aliasing can be seen in native imaging in the e' wave at the base. In harmonic imaging, there is aliasing both in the S' wave, and the e' wave (double).	Colour tissue Doppler curved M-mode in harmonic imaging, velocity plot (above), strain rate (below). As can be seen there is heavy aliasing in the velocity plot, but no aliasing in strain rate imaging.

However, this would imply that separate recordings had to be taken for strain rate and velocity analysis, instead of post processing strain rate from TDI recordings, but might improve the reverberation sensitivity of strain rate imaging by tissue Doppler.

Shadowy reverberations covering the anterior wall in this 2-chamber image. It is differentiated from drop out, as we can se a "fog" of structures covering the anterior wall. The structures are stationary. This is not distinct reverberations shadows, but incoherent clutter.

Recordings from the basal anterior ring of the subject to the left. The true signal is clearly visible as a normal curve, and can be seen separately from the clutter band, which is the horizontal spectral band along the baseline. The colour Doppler recording is superposed and aligned with both vertical and horizontal scale. The colour Doppler, using the autocorrelation algorithm, results in mean velocities that incorporate both signal and clutter, giving a severe underestimation of velocities.

This example is different from a simple drop out, as pw tissue Doppler curves from the same examination show normal peak velocities in the anterior wall as shown below. Once again spectral Doppler is able to overcome the clutter problem, showing true peak mitral ring systolic velocities of 8.5 cm/s, compared to the peak values of 2 cm/s seen by colour Doppler above.


Basal spectral tissue Doppler curve in the anterior wall. Peak systolic velocity ca 8.5 cm/s.	Midwall spectral tissue Doppler curve in the anterior wall. Peak systolic velocity ca 6.5 cm/s.	Apcal spectral tissue Doppler curve in the anterior wall. Peak systolic velocity ca 5 cm/s.

From this, it would seem that clutter is solely non-random noise, but in fact they also increases (relative) random noise.

Basically clutter is stationary echoes resulting in zero velocities as described more in detail in the basic ultrasound section. Thus, cutter is basically systematic noise, not random. However, in colour tissue Doppler clutter will also lead to increase in random noise. This is again due to the autocorrelation algorithm. The velocity estimate in each pixel will be an average of the amount of clutter and of moving echoes. The final velocity estimate will vary according to the relative amplitude of the clutter and the moving echo (weighted) (284), and this varies according to the speckle pattern as described here. Thus, in areas with much clutter, the velocity variations are larger than in high quality recordings:


IColour M-mode from the image shown above. The curved M-mode shows a fairly homogenous and normal signal in the inferior wall (top), but more or less random noise in the anterior wall (bottom), where the noise is seen as vertical stripes of alternating colours.	Velocity curves from the anterior wall, showing noise, and not much more, but at low level (within ± 0.3 cm/s).

The principle of the effect of clutter. V-plot with clutter showing how the mean velocities are reduced, compared to the mormal expected values (red line). But in additions the variation of the velocity estimates from pixel to pixel is much higher, resulting in increased noise, but with reduced mean values.	Combined pulsed Doppler (yellow bands) and colour Doppler green Aligned horizontally and vertically. The noise level can be seen to be b´very low, compared to the peak velocities shown in the pulsed Doppler recording. The clutter is the horizontal band around the baseline, and the width of the spectrum in this case is the noise.

Further examples are shown below:


Reverberations in the septum of a normal ventricle. The colour bands are stationary	In pulsed wave tissue Doppler, the clutter will show up as a high amplitude band of zero velocities, but the true velocity curves can be seen as entirely separate from the clutter line, and thus peak velocities can still be measured.

Colour Doppler, calculating average velocities, will average in the clutter. Looking at the same example as above, we see the difference in peak values:

Velocity curves from the reverberations shown in the video above. Left colour Doppler from three sites showing peak systolic values of about 3, 2 and 1 cm/s, respectively. The pulsed Doppler recordings from the same sites separates the clutter from the velocity signal, and thus we find peak systolic velocities of about 12, 11 and 8 cm/s, respectively. Normally the systematic difference between the two methods is only about 1.5 - 2 cm/s as shown in the HUNT study.

Thus, maximum values are more robust in relation to artifacts than both taking the middle of the spectrum and than colour tissue Doppler, but the spectrum width will lead to som overestimation of peak values:

For the present, the best compromise seems to be: pw Tissue Doppler should be measured as maximal values, but with the lowest possible gain setting.

Autocorrelation velocities may be influenced by reverberations (clutter). The mechanism for the formation of reverberations are explained in the basic ultrasound section.

The principle of clutter effect on spectral and autocorrelation velocities. In this simulation, an ordinary spectral celocity cirve is seen. The peak velocities depend on the width of the spectrum as shown above. The modal velocity is the middle of the spectrum. A stationary clutter band ois added, with zero velocities, and with nearly the same amplitude and spectrum width. The modal velocity is the zero line. The autocorrelation in this case will then be the average of both, far removed from the true modal velocity curve.

Image from another subject in the study shown above (240). In this subjech there is some clutter from reverberations, as seen by the band in systole close to the zero line. In this case the peak velocity by autocorrelation is lower than the modal velocity of the main spectral band, which still was the one closest to the RF M-mode reference. (Figure courtesy of Svein Arne Aase)

Clutter filtering may reduce the problem, as seen here. There is a band of clutter close to zero velocities, but as seen here, the spectral modality makes it very easy to separate the true and clutter velocities. However, the clutter affects the autocorrelation velocity (red line), giving lower velocities, but with clutter filter this effect is removed (red line) , and the peak value is substantially higher. Image modified from (243).

Ultra high frame rate tissue Doppler (UFR-TDI)

Ultra high frame rate tissue Doppler is done by combining more principles:

Using very little focussing (planar beams). This is feasible as tissue Doppler doesn't use harmonic imaging
Planar beams allows a high MLA factor. Again, this is feasible as tissue Doppler is about acquiring numerical values, not pretty images.
Broad beams and high MLA factor allows the whole of one wall to be covered by one transmit beam.
Designing the software so there is only sent one transmit beam along each wall per frame, i.e. only two pulses per frame. This is the extreme example of exchanging spatial for temporal resolution.

By this method, using two broad, unfocussed (planar) beams, each covering one wall, as well as 16 MLA and sparse interleaved B-mode imaging, it has proved possible to increase the TDI frame rate substatially (172, 268). it has been possible to increase frame rate to 1200 FPS in 2D imaging.

Few beams give high frame rate. Image courtesy of Svein Arne Aase, modified from (172).

Already this has shown new information about both the pre ejection and post ejection dynamics.

With this method, it is possible to acquire IQ (RF) data with FR > 1000. This makes it possible to process restrospective tissue Doppler from the whole field (i.e. that covered by the two transmit beams), simultaneously from one heart cycle. as in colour Doppler.

Retrospective spectral Doppler curves from base, midwall and apex, all acquired from the same heart cycle, showing the decreasing velocities from base (1) to apex (3). The simultaneity of Doppler data from the whole field, allows the velocity gradient to be imaged below, as in colour Doppler. This gradient is taken from the window in mid systole shown in the top left. Image courtesy of Lars Christian Naterstad Lervik.

This allows thequalitative assessment of strain rate from Doppler curves, construction of a V-plot, and all relatively unaffected by clutter, as described in principle above and in the pitfalls section.

The V-plot, derived from autocorrelation, is vulnerable to clutter and drop outs, as decribed in the pitfalls section. this means that the V-plots are difficult to see differences between artefacts and pathology.

However, with Ultra high frame rate tissue Doppler (UFR-TDI), it is possible to process restrospective tissue Doppler from the whole field simultaneously, which means that not only will tissue Doppler be available that are relatively unaffected by clutter noise, but also that spectral V-plots can be processed, which shares the reduced vulnerability to clutter as shown in the pitfalls section.

Spectral Doppler V-plot, analoguous to the one above. With retrospective spectrral Doppler the velocities are available simultaneously over the whole field, as with colour Doppler, meaning that the spatial velocity gradients are available. The reconstructed curves with decreasing velocities from base to apex are shown top right. This means that strain rate can be visualised by the slope of the V-plot. There is substantial clutter in the lateral wall, but this is irrelevant for the slope, being related to the peak values of the spectrum. However, as seen here, the window for the V-plot is mid systolic, and thus lower than the peak systolic, and so is the slope. being lower than peak strain rate. Image courtesy of Lars Christian Naterstad Lervik.

With V-plots infarcts are seen as a reduction in the slope of the V-plot, as in colour Doppler.

.
Spectral V-plot from two-chamber view. There is reduced strain rate in the two basal inferior segments, with hyperkinesia in the apical, and normal strain rate in the anterior wall. There is moderate clutter in the anterior wall, which is irrelevant. Again, the values are mid systolic, not peak systolic.

3-dimensional tissue Doppler

Tissue Doppler is still limited to one velocity direction only. This means that the term "3-dimensional" refers to a three dimensional distribution of tissue velocities only, not velocity vectors in a three dimensional coordinate system. However, data from the whole ventricle can be put together on a surface model of the left ventricle.


3D tissue Doppler is basically a grid of numerical values on a ventrricular surface.	Triplane tissue Doppler, showing three standard planes, with the assumption that the angle between them is 60°, the rest of the data between the planes are than interpolated. This gives a circumferential resolution of 60°.

As tissue data as about acquiring (and displaying, f.i. by colour) numerical data, the method do not have the same limitation as 3D B-mode. One method is to combine information from three standard planes, and then interpolating the data between the planes by for instance spline. The method has been explained elsewhere. This has been done both by combining sequentially acquired standard planes. It could also be done as a simultaneous triplane acquisition, but at the cost of a substantially reduced frame rate. Thus, freehand scanning has been preferred.

Systolic (left) and early diastolic (right) frame showing the 3D surface of the left ventricle, where longitudinal tissue Doppler values are displayed with colour. Red shows velocities toward the apex, blue velocities away from the apex. (mark the colour gradient from base to apex, reflecting the velocity gradient).

This version of three dimensional tissue Doppler may be used for display, but also for area measurement, as the data are distributed over a representation of the (approximate) real ventricular area.

With the Ultra high frame rate tissue Doppler method, it is also possible to acquire three dimensional tissue Doppler in real time.

Using a 3D matrix probe, sending an array of 3x3 broad unfocussed or planar beams, and using a 4x4 matrix of receive beams for each transmit beam, giving a 16 (or 4x4) MLA, we have been able to achieve a volume rate of about 500 VPS (280), i.e. Ultra high frame rate 3D tissue Doppler.


Principle of beam formation, showing a matrix of 3x3 wide transmit beams (brown circles) and for each beam an array of 4x4 receive beams, i.e. a 16 MLA. (After 280).	Distribution of the transmit beams in relation to a cross section of the ventricle, endocardial and epicardial surfaces marked with black lines and arrows. the energu distribution of the beams is shown by the colour hue. The transverse plane shown to the right is marked by the thick line. (After 280).	Distribution of the transmit beams in an apical plane, the level of the cross section to the left is marked by the thick line. As evident from the illustration, the transmit beams do not cover the whole sector, but will cover most of the walls. (After 280).

By this method, t is possible to achieve a high circumferential resolution through the MLA technique at the same time as a high temporal resolution. The result can be displaued as a 3D figure, as with reconstructed 3D, and both curved M-modes and tivelocity curves can be extracted from this matrix:



3D surface with tissue velocity display. The ring represents a line for extraction of the curved M-mode shown top, left. (After 280).	Data display from the 3D velocity figure to the right. Top: curved M-mode, showing the time variation of apically directed velocities in a ring around the mid ventricle. Bottom, velocity curves from the basolateral part, red from UFR 3D TVI, extracted from the 3D data to the left, blue velocity from the same point in the same subject, but acquired bt conventional colur TDI (i.e. a different heartbeat).

Material	Velocity ( m/s)
Air	330
Water	1497
Fat	1440
Average soft tissue	1540
Blood	1570
Muscle	1500 - 1630
Bone	2700 - 4100
Metal	3000 - 6000

Material interface	Reflection coefficient
Liver/Kidney	0.006
Kidney/spleen	0.003
Blood/Kidney	0.009
Liver/fat	0.11
Liver/Bone	0.59
Liver /Air	0.9995


The return pulse is a waveform. To process this, multiple samples along the waveform is needed. However, if the full waveform is stored, both amplitude and frequency can be post processed.	The pulse has a certain amplitude, depending on how much energy that is reflected	And the amplitude information is only a single value that is represented without furthwer information of the waveform. This is the only data that are used in B-mode and M-mode imaging	In addition to the amplitude, the wave frequency can be stored as additional information of the waveform, but still a fairly simple dataset. This additional information that can be used in Doppler.

Tissue	Attenuation (Db / cm /MHz)
Water	0.02
Blood	0.15
Liver	0.40
Brain	0.44
Muscle	0.57
Bone	22


Illustration of effects of shadows on an ultrasound beam. Left: no shadow. Middle, a shadow distant from the beam (e.g. a calcification or the lung seen at a distance), resulting in a shadow with no image below it. Right a shadow close to the transducer surface (e.g. lung edge or rib) will result in a narrow beam (reduced apparent aperture) which will not be seen as a shadow in the picture, but rather a reduced lateral resolution. (Original simulation image to the left courtesy of Hans Torp, modifications by me.) The effect of the depth of the origin of the shadows in the images is shown below, indicated by the green arrows.

Left, shadow originating at a depth of ca 3 cm, as can seen by the visible structures of the chest wall closer to the probe. The shadow is probably due to the edge of the lung. Right; a small repositioning of the probe solves the problem.	Left shadow originating close to the chest wall (< 1 cm), probably the edge of a costa. It can be seen as a shadow, but the main effect is loss of lateral resolution in the shadow, and again a small repositioning of the probe solves the problem as seen to the right.

more pronounced drop out of the anterior wall in this 2-chamber view due to a lung shadow distant from the probe. However, the lateral resolution may be seen to be reduced at the basal part of the border between the picture and the shadow.	Reduced lateral resolution due to costal shadow. The effects of both costae and shadows will vary, according to the distance from the probe. In this case the patient was extremely thin, thus there was virtually no distance between the probe and the costa. In this case, no localised shadow can be seen, the costa was to the left in the image, where resolution is poorest.


Signal intensity is attenuated exponentially by depth as shown by this curve.	Attenuation can be measured in decibels (logarithmic scale) as a function of depth, the decibel scale will be linear


Calcification in the posterior mitral ring seen both in parasternal and apical views from the same patient. The shadow is clearly visible in both views.


Uncompensated image, showing decreasing signal intensity (and, hence, visibility) with depth, due to attenuation.	Increasing over all gain, will increase the amplitude of the signal, and the structures at the bottom of the sector becomes more visible. But the gain in the top of the sector are also increased, including the cavity noise, thus decreasing contast in this part of the image.

TGC controls. Basically, each slider controls gain selectively at a certain depth:	In older models, the TGC should be set manually to achieve a balanced image:


Present models, however, have automatic TGC. Thus the default control setting should be neutral to achieve a balanced picture:	Using manual setting by old habit will result in a double compensation, with too much gain in the bottom, too little in the top:


Image with default gain, reject and compress settings	Principle of gain, reject and compress. All curves display brightness of the display in relation to the amplitude of the rejected signal. An ordinary gain curve is shown in black, using a linear brightness scale, displays the full range of amplitudes. Increasing gain (red curve), will increase all signals, including the weakest, as in the noise. The disadvantage, in addition to increasing noise, is that the strongest signals will be saturated, so details may disappear. Compress is shown as the blue curve. This results in a steeper brightness curve, resulting in less brightness of the weakest echoes, and more brightness of the strongest. Thus, weak echoes may disappear together with background noise, while strong echoes will be saturated, resulting in loss of detail. Finally reject is shown by the light grey zone, siply displaying all signals below a certain amplitude as black. (The black brightnes curve drops abruptly to zero at the reject limit (dark grey line). A combination of high gain and reject will give an effect fairly similar to the compress function.


Same image with high gain (top) showing increased density of the endocardium, but loss of detail due to brightness saturation and a corresponding increase in cavity noise and low gain (bottom), showing reduction in cavity noise, but loss of detail (see endocardium in lateral wall).	Same image with increased reject (top) showing reduction in cavity noise, but also with slight loss of detail (endocardium in lateral wall) and compress function (bottom) with less detail in the myocardium due to increased brightness.


Effect of angulation in thickness measurement. The true thickness is L₀, the measurement, however may be done along an M-mode beam parallel to the length L. As the cosine to the angle between them is defined as cos ( ) = L₀ / L, the true length L₀ is overestimated by the cosine to the angle, the measured line is the true line divided by the cosine to the angle.	Example from reconstructed M-mode, with vertical scales aligned at zero and 6 cm depth for comparison. To the left, the line crosses the septum transversely resulting in a diastolic thickness measure of 7mm, to the right the M-mode line is skewed, and the measurement across the septum is longer (10 mm).


Reconstructed M-mode with a fairly straight cross angle between the M-mode line and the LV long axis.	Reconstructed M-mode from the same loop, but with the M-mode line crossing the LV long axis at a skewed angle, showing thicker walls and wider cavity, due to the angulation.


1. The randomness of the speckle pattern ensures that each region of the myocardium has its own unique speckle pattern: that can differentiate a region from other region	2. The speckle pattern remains reasonably stable, and the speckles follow the myocardial motion. This can be demonstrated by M-mode, showing how the speckle pattern follows the myocardial motion.	Defining a kernel in the myocardium will define a speckle pattern within (red). Within a defined search area ( blue), the new position of the kernel in the next frame (green) can be recognised by finding the matchin speckle pattern in a new position. The movement of the kernel (thick blue arrow) can then be measured.	Speckle tracking search algorithm. The kernel is defined in the original frame at t=0 (red square). In the next frame, at t=t, the algorithm defines a search area (white square), and the search is conducted in all directions for the matching kernel.


LOngitudinal speckle tracking in apical 4 chamber view. The resulting tracking of the kernels shown in motion. As can be seen, with a drop out apicolateral, this ROI tracks less than perfect, giving too low strain both in LA and MA segments.	Speckle tracking can be applied crosswise. In this parasternal long axis view, the myocardial motion is tracked both in axial and transverse (longitudinal) direction. It is evident that the tracking is far poorer in the inferior wall, due to the poor lateral resolution at greater depth.


The kernel is in a reverberation in the lateral wall, and will not track, thus both the segment below and above the reverberation will show artefacts.	Adjusting the position of the kernel manually, allows speckle tracking despite the reverberation, if the kernel remains outside the reverberation during the whole heart cycle.


Christian Andreas Doppler	Christophorus Henricus Diedericus Buys-Ballot
Über das farbige Licht der Doppelsterne und einiger anderer Gestirne des Himmels. Abhandlungen der königl. Böhm. Gesellschaft der Wissenschaften. 1843; 2: 465-82 Versuch einer das Bradely'sche Aberrations-theorem als integrirenden theil in sich schliessenden allgemeineren Theorie	Akustische Versuche auf der Niederländischen Eisenbahn nebst gelegentlichen Bemerkungen zur Theorie des Hrn. Prof. Doppler. Poggendorfs Annalen der Phüsik und Chemie 1845; 66: 321-351

Strain rate imaging.