3 Deformation

Strain is the term introduced in continuum mechanics for local deformation in a material, i.e., deformation in the neighborhood of a particle. Such local deformation is normally represented by changes in material lines, angles and volume. Correspondingly, three primary measures of strain is introduced; longitudinal strain $ \epsilon $, shear strain $ \gamma $, and volumetric strain $ \epsilon_v $.

3.1 Measures of strain

Figure 17: Deformation of a body by relating the current configuration ($ K,t $) to the reference configuration($ K_0,t_0 $.

In Figure 17 a body is represented in the current configuration $ K $ at time $ t $ and in the reference configuration $ K_0 $ at time $ t_0 $. The position of an arbitrary particle, denoted $ P $, in the body in the current configuration $ K $ is given by $ \boldsymbol{r}(\boldsymbol{r}_0,t) $, where $ \boldsymbol{r}_0 $ is the location of the same particle, denoted $ P_0 $, in the reference configuration $ K_0 $. The set of coordinates of $ \boldsymbol{r}_0 $ is conventionally denoted $ X $ with corresponding spatial components $ X_1,X_2,X_3 $. The terms location and particle are used interchangeably for convenience, and thus we may refer to the particle $ \boldsymbol{r}_0 $ or the particle $ X $.

The vector $ \boldsymbol{r}(\boldsymbol{r}_0,t) $ is a function which represents the motion of an arbitrary particle in the body, which originally had the position $ \boldsymbol{r}_0 $. It may also be thought of as a map between the reference and current configuration. The motion may be represented as vector valued function or by its components: $$ \begin{equation} \boldsymbol{r} = \boldsymbol{r}(\boldsymbol{r}_0,t) \Leftrightarrow x_i = x_i(X,t) \tag{3.1} \end{equation} $$

The displacement vector $ \boldsymbol{u}(\boldsymbol{r}_0,t) $ (see Figure 17 ) is also a function which represents motion relative to the original location: $$ \begin{equation} \boldsymbol{u}(\boldsymbol{r}_0,t) = \boldsymbol{r}(\boldsymbol{r}_0,t)-\boldsymbol{r}_0 \tag{3.2} \end{equation} $$

Figure 18: Deformation of a body from the current configuration ($ K,t $) to the reference configuration($ K_0,t_0 $.

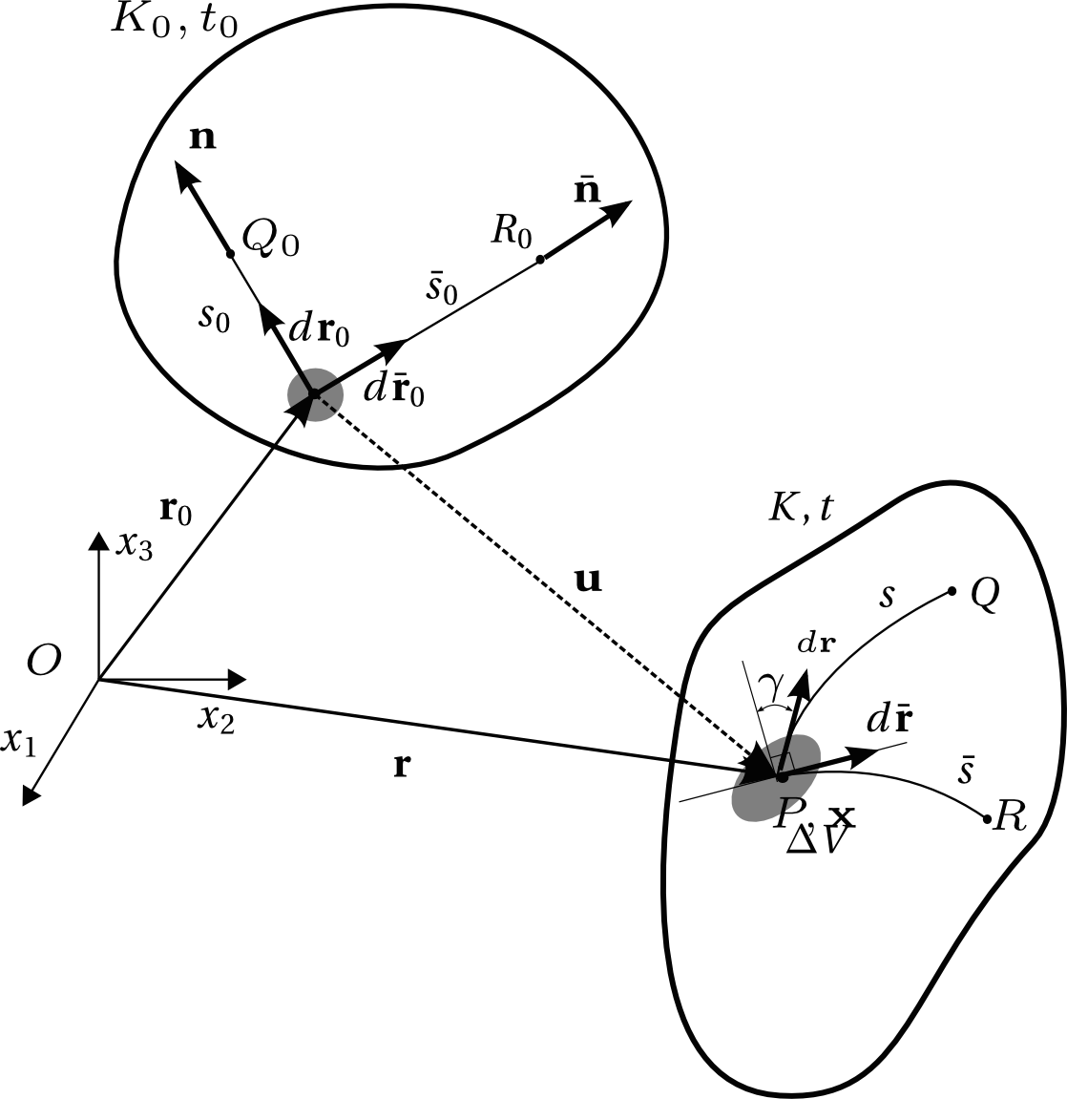
Let $ P_0 $ denote the point with coordinates $ \bf{r}_0 $ in$K_0$ Let $ s_0=P_0Q_0 $ denote the length the straight line from $ P_0 $ to $ Q_0 $ in the reference configuration $ K_0 $ from $ \bf{r}_0 $ in the direction of $ \boldsymbol{n} $. In general this line will change both form and length in the current configuration $ K $, where its length is represented by $ s=PQ $. Definitions of the three measures strain may then be formulated:

Longitudinal strain $ \epsilon $ The longitudinal strain $ \epsilon $ in the direction $ \boldsymbol{n} $ in a particle $ \boldsymbol{r}_0 $ is defined by: $$ \begin{equation} \epsilon= \lim_{s_0 \rightarrow 0} \frac{s-s_0}{s_0} = \frac{d s - d s_0}{d s_0} = \frac{d s}{d s_0} -1 \tag{3.3} \end{equation} $$

The longitudinal strain $ \epsilon $ represents the change of length per unit length in the direction of $ \boldsymbol{n} $ in particle $ \boldsymbol{r}_0 $.

Figure 18 illustrates the same situation as in Figure 17, albeit with some more details, allowing for the definition of shear strain:

Shear strain $ \gamma $ The angular deviation (in radians) from $ \pi/2 $ between two material lines in $ K $ which originally were perpendicular in $ K_0 $. The shear strain $ \gamma $, is taken to be positive when the angle is reduced.

In Figure 18, the shear strain $ \gamma $ is illustrated at the location $ \mathbf{r}_0 $, as the angular deviation from $ \pi/2 $ between $ \mathbf{n} $ and $ \mathbf{\bar{n}} $, two perpendicular material line elements in the reference configuration $ K_0 $.

Volumetric strain $ \epsilon_v $ $$ \begin{equation} \epsilon _v = \mathop {\lim }\limits_{\Delta V_0 \to 0} \frac{{\Delta V - \Delta V_0 }}{{\Delta V_0 }} \tag{3.4} \end{equation} $$

The volumetric strain $ \epsilon_v $ represents change in a differential volume per unit undeformed differential volume around the particle $ \boldsymbol{r}_0 $.

In the following, commonly used expressions for the primary measures of strain will be introduced.