Example 2.6: Balance Laws
In this example we will solve a scalar conservation law with a source

numerically by operator splitting. To this end, we use two substeps,

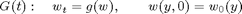
and construct the approximate solution from the formula
![$$u(x,t)\approx [G(\Delta t)\circ S(\Delta t) ]^n u_0(x)$$](Example2_6_eq79590.png)
The hyperbolic step will be solved using the Lax-Friedrichs scheme and the ODE will be solved using MATLAB's ode45, which is a standard Runge-Kutta solver for nonstiff ODEs.
Initial setup
T = 12;
N = 512;
h = 2*pi/N;
x = -pi+(0:N)*h; x=0.5*(x(1:end-1)+x(2:end));
u0 = exp(-4*sin((x+2)/2).^2);
h = path; path(h,'../Example2_5');
Burgers' equation with nonlinear source
As a concrete example we will use Burgers' equation with a nonlinear source term
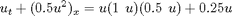
and periodic boundary conditions.
First, we plot the flux function and the nonlinear source function
u = linspace(0,1.31,101); plot(u, flux(u), u, source(0,u)), axis tight, legend('flux','source',2)

Evolution of the shock profile
nsplit = 200; u = sourcesplit('flux', 'source', u0, x, T, nsplit); subplot(2,1,1), contourf(x,linspace(0,T,nsplit+1),u',20), colorbar subplot(2,1,2), surf(x,linspace(0,T,nsplit+1),u') shading interp; view(-10,50), axis tight

The initial smooth profile starts to travel to the right and sharpens up into a travelling shock wave followed by a rarefaction. Because of the nonlinear shape of the source term, we have negative accumulation in front of the shock (where u<0.2) and positive accumulation in the rarefaction (where u>0.2). Around t=6.5, the shock leaves the domain at the right-hand side and re-enters it at the left-hand side. The shock front then overtakes the rarefaction wave and the solution converges to the stationary solution u=1.3090..
Compare different time steps
Having established the dynamics of the problem, we can investigate the performance of our numerical method for different choices of the splitting step.
for n=1:4, nsplit = 8*4.^(n-1); u = sourcesplit('flux','source',u0,x,T,nsplit); subplot(2,2,n); contourf(x,linspace(0,T,nsplit+1),u'); xlabel('x'), ylabel('time'), colorbar title([num2str(nsplit) ' steps']) end path(h);

Even with only eight splitting steps, we are able to capture the major trends of the evolutionary behavior of our problem. However, to get rid of the artificial staircase behavior of the evoloving shock, we need to increase the number of splitting steps quite high.