TMM4175 Polymer Composites

Home About Python Links Table of Contents

Laminate loads and constitutive relations¶

Due to the discontinuous variation of stresses from layer to layer, we will conveniently consider the integrated effect of the stresses on the laminate. The laminate loads acting on a laminate are the in-plane forces $N_x$, $N_y$ and $N_{xy}$, and the moments $M_x$, $M_y$ and $M_{xy}$ as illustrated in Figure-1.

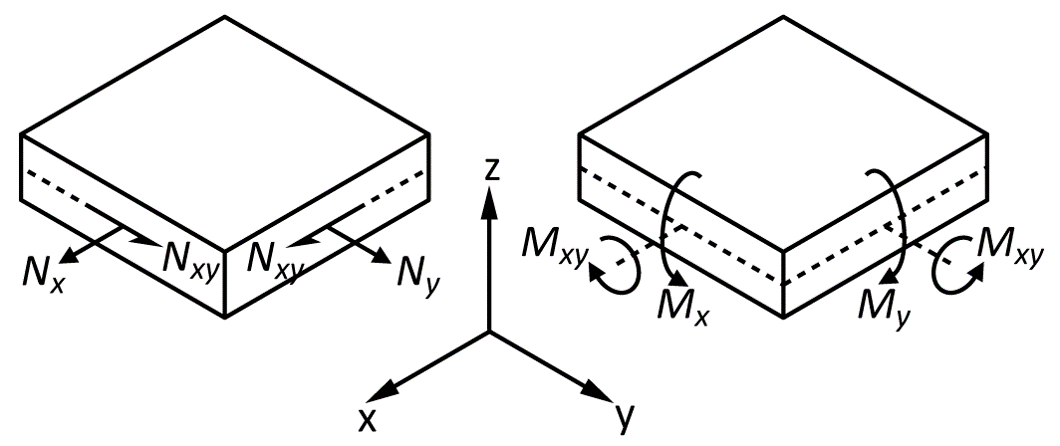
Figure-1: Laminate loads

Force resultants¶

The in-plane forces per unit length on individual layers are \begin{equation} N_{x,k}=\int_{h_{k-1}}^{h_k} \sigma_x dz, \quad N_{y,k}=\int_{h_{k-1}}^{h_k} \sigma_y dz, \quad N_{xy,k}=\int_{h_{k-1}}^{h_k} \tau_{xy} dz \tag{1} \end{equation}

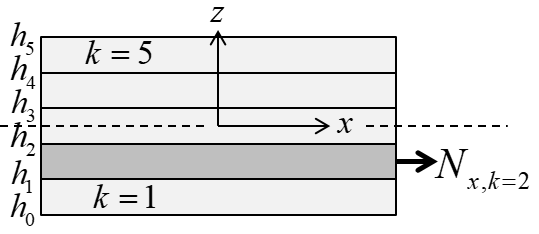
Figure-2: Force per unit length of a single layer

The resultant forces per unit length on the laminate is the sum of contributions from all layers:

\begin{equation} N_{x}=\sum_{k=1}^{n} \int_{h_{k-1}}^{h_k} \sigma_x dz, \quad N_{y}=\sum_{k=1}^{n} \int_{h_{k-1}}^{h_k} \sigma_y dz, \quad N_{xy}=\sum_{k=1}^{n} \int_{h_{k-1}}^{h_k} \tau_{xy} dz \tag{2} \end{equation}

Equation (2) can be expressed in matrix form as

\begin{equation} \begin{bmatrix} N_x \\ N_y \\ N_{xy} \end{bmatrix} = \sum_{k=1}^{n} \int_{h_{k-1}}^{h_k} \begin{bmatrix} \sigma_x \\ \sigma_y \\ \tau_{xy} \end{bmatrix} dz \tag{3} \end{equation}

The stresses can now be expressed through Hooke's law for the plane stress case:

\begin{equation} \begin{bmatrix} N_x \\ N_y \\ N_{xy} \end{bmatrix} = \sum_{k=1}^{n} \int_{h_{k-1}}^{h_k} \begin{bmatrix} Q_{xx} & Q_{xy} & Q_{xs} \\ Q_{xy} & Q_{yy} & Q_{ys} \\ Q_{xs} & Q_{ys} & Q_{ss} \end{bmatrix}_k \begin{bmatrix} \varepsilon_x \\ \varepsilon_y \\ \gamma_{xy} \end{bmatrix} dz \tag{4} \end{equation}

Recall from Laminate deformation that the strain at a position $z$ is

\begin{equation} \begin{bmatrix} \varepsilon_x \\ \varepsilon_y \\ \gamma_{xy} \end{bmatrix}= \begin{bmatrix} \varepsilon_x^0 \\ \varepsilon_y^0 \\ \gamma_{xy}^0 \end{bmatrix}+z \begin{bmatrix} \kappa_x \\ \kappa_y \\ \kappa_{xy} \end{bmatrix} \tag{5} \end{equation}

Substituting (5) into (4) yields:

\begin{equation} \begin{bmatrix} N_x \\ N_y \\ N_{xy} \end{bmatrix} = \sum_{k=1}^{n} \int_{h_{k-1}}^{h_k} \begin{bmatrix} Q_{xx} & Q_{xy} & Q_{xs} \\ Q_{xy} & Q_{yy} & Q_{ys} \\ Q_{xs} & Q_{ys} & Q_{ss} \end{bmatrix}_k \begin{bmatrix} \varepsilon_x^0 \\ \varepsilon_y^0 \\ \gamma_{xy}^0 \end{bmatrix} dz + \sum_{k=1}^{n} \int_{h_{k-1}}^{h_k} \begin{bmatrix} Q_{xx} & Q_{xy} & Q_{xs} \\ Q_{xy} & Q_{yy} & Q_{ys} \\ Q_{xs} & Q_{ys} & Q_{ss} \end{bmatrix}_k \begin{bmatrix} \kappa_x \\ \kappa_y \\ \kappa_{xy} \end{bmatrix} z dz \tag{6} \end{equation}

Since the stiffness matrix, mid-plane strains and curvatures do not vary through the thickness of a layer, equation (6) can be rearranged to

\begin{equation} \begin{bmatrix} N_x \\ N_y \\ N_{xy} \end{bmatrix} = \sum_{k=1}^{n} \begin{bmatrix} Q_{xx} & Q_{xy} & Q_{xs} \\ Q_{xy} & Q_{yy} & Q_{ys} \\ Q_{xs} & Q_{ys} & Q_{ss} \end{bmatrix}_k \begin{bmatrix} \varepsilon_x^0 \\ \varepsilon_y^0 \\ \gamma_{xy}^0 \end{bmatrix} \int_{h_{k-1}}^{h_k} dz + \sum_{k=1}^{n} \begin{bmatrix} Q_{xx} & Q_{xy} & Q_{xs} \\ Q_{xy} & Q_{yy} & Q_{ys} \\ Q_{xs} & Q_{ys} & Q_{ss} \end{bmatrix}_k \begin{bmatrix} \kappa_x \\ \kappa_y \\ \kappa_{xy} \end{bmatrix} \int_{h_{k-1}}^{h_k} z dz \tag{7} \end{equation}

Performing the integrations,

\begin{equation} \int_{h_{k-1}}^{h_k} dz = h_k - h_{k-1}, \quad \int_{h_{k-1}}^{h_k}z dz = \frac{1}{2}(h_k^2 - h_{k-1}^2) \tag{8} \end{equation}

such that equation (7) can written as

\begin{equation} \begin{bmatrix} N_x \\ N_y \\ N_{xy} \end{bmatrix} = \sum_{k=1}^{n} \begin{bmatrix} Q_{xx} & Q_{xy} & Q_{xs} \\ Q_{xy} & Q_{yy} & Q_{ys} \\ Q_{xs} & Q_{ys} & Q_{ss} \end{bmatrix}_k \begin{bmatrix} \varepsilon_x^0 \\ \varepsilon_y^0 \\ \gamma_{xy}^0 \end{bmatrix} (h_k - h_{k-1}) + \frac{1}{2} \sum_{k=1}^{n} \begin{bmatrix} Q_{xx} & Q_{xy} & Q_{xs} \\ Q_{xy} & Q_{yy} & Q_{ys} \\ Q_{xs} & Q_{ys} & Q_{ss} \end{bmatrix}_k \begin{bmatrix} \kappa_x \\ \kappa_y \\ \kappa_{xy} \end{bmatrix} (h_k^2 - h_{k-1}^2) \tag{9} \end{equation}

Now defining

\begin{equation} \begin{bmatrix} A_{xx} & A_{xy} & A_{xs} \\ A_{xy} & A_{yy} & A_{ys} \\ A_{xs} & A_{ys} & A_{ss} \end{bmatrix}= \sum_{k=1}^{n} \begin{bmatrix} Q_{xx} & Q_{xy} & Q_{xs} \\ Q_{xy} & Q_{yy} & Q_{ys} \\ Q_{xs} & Q_{ys} & Q_{ss} \end{bmatrix}_k (h_k - h_{k-1}) \tag{10} \end{equation}

and

\begin{equation} \begin{bmatrix} B_{xx} & B_{xy} & B_{xs} \\ B_{xy} & B_{yy} & B_{ys} \\ B_{xs} & B_{ys} & B_{ss} \end{bmatrix} = \frac{1}{2} \sum_{k=1}^{n} \begin{bmatrix} Q_{xx} & Q_{xy} & Q_{xs} \\ Q_{xy} & Q_{yy} & Q_{ys} \\ Q_{xs} & Q_{ys} & Q_{ss} \end{bmatrix}_k (h_k^2 - h_{k-1}^2) \tag{11} \end{equation}

and finally equation (9) becomes

\begin{equation} \begin{bmatrix} N_x \\ N_y \\ N_{xy} \end{bmatrix} = \begin{bmatrix} A_{xx} & A_{xy} & A_{xs} \\ A_{xy} & A_{yy} & A_{ys} \\ A_{xs} & A_{ys} & A_{ss} \end{bmatrix} \begin{bmatrix} \varepsilon_x^0 \\ \varepsilon_y^0 \\ \gamma_{xy}^0 \end{bmatrix}+ \begin{bmatrix} B_{xx} & B_{xy} & B_{xs} \\ B_{xy} & B_{yy} & B_{ys} \\ B_{xs} & B_{ys} & B_{ss} \end{bmatrix} \begin{bmatrix} \kappa_x \\ \kappa_y \\ \kappa_{xy} \end{bmatrix} \tag{12} \end{equation}

Moment resultants¶

Correspondingly, resultant moments per unit length are:

\begin{equation} \begin{bmatrix} M_x \\ M_y \\ M_{xy} \end{bmatrix} = \sum_{k=1}^{n} \int_{h_{k-1}}^{h_k} \begin{bmatrix} \sigma_x \\ \sigma_y \\ \tau_{xy} \end{bmatrix}z dz \tag{13} \end{equation}

Substitution and integration leads to

\begin{equation} \begin{bmatrix} M_x \\ M_y \\ M_{xy} \end{bmatrix} = \begin{bmatrix} B_{xx} & B_{xy} & B_{xs} \\ B_{xy} & B_{yy} & B_{ys} \\ B_{xs} & B_{ys} & B_{ss} \end{bmatrix} \begin{bmatrix} \varepsilon_x^0 \\ \varepsilon_y^0 \\ \gamma_{xy}^0 \end{bmatrix}+ \begin{bmatrix} D_{xx} & D_{xy} & D_{xs} \\ D_{xy} & D_{yy} & D_{ys} \\ D_{xs} & D_{ys} & D_{ss} \end{bmatrix} \begin{bmatrix} \kappa_x \\ \kappa_y \\ \kappa_{xy} \end{bmatrix} \tag{14} \end{equation}

where

\begin{equation} \begin{bmatrix} D_{xx} & D_{xy} & D_{xs} \\ D_{xy} & D_{yy} & D_{ys} \\ D_{xs} & D_{ys} & D_{ss} \end{bmatrix} = \frac{1}{3} \sum_{k=1}^{n} \begin{bmatrix} Q_{xx} & Q_{xy} & Q_{xs} \\ Q_{xy} & Q_{yy} & Q_{ys} \\ Q_{xs} & Q_{ys} & Q_{ss} \end{bmatrix}_k (h_k^3 - h_{k-1}^3) \tag{15} \end{equation}

Equations (12) and (14) can now be combined into

\begin{equation} \begin{bmatrix} N_x \\ N_y \\ N_{xy} \\ M_x \\ M_y \\ M_{xy} \end{bmatrix} = \begin{bmatrix} A_{xx} & A_{xy} & A_{xs} & B_{xx} & B_{xy} & B_{xs} \\ A_{xy} & A_{yy} & A_{ys} & B_{xy} & B_{yy} & B_{ys} \\ A_{xs} & A_{ys} & A_{ss} & B_{xs} & B_{ys} & B_{ss} \\ B_{xx} & B_{xy} & B_{xs} & D_{xx} & D_{xy} & D_{xs} \\ B_{xy} & B_{yy} & B_{ys} & D_{xy} & D_{yy} & D_{ys} \\ B_{xs} & B_{ys} & B_{ss} & D_{xs} & D_{ys} & D_{ss} \end{bmatrix} \begin{bmatrix} \varepsilon_x^0 \\ \varepsilon_y^0 \\ \gamma_{xy}^0 \\ \kappa_x \\ \kappa_y \\ \kappa_{xy} \end{bmatrix} \tag{16} \end{equation}

Summary¶

Force resultants: $$ \mathbf{N} = \sum_{k=1}^{n} \int_{h_{k-1}}^h \boldsymbol{\sigma}'dz = \sum_{k=1}^{n} \int_{h_{k-1}}^h \mathbf{Q}'_k\boldsymbol{\varepsilon}'dz = \sum_{k=1}^{n} \int_{h_{k-1}}^h \mathbf{Q}'_k(\boldsymbol{\varepsilon}^0 + z \boldsymbol{\kappa})dz = \sum_{k=1}^{n} \int_{h_{k-1}}^h \mathbf{Q}'_k\boldsymbol{\varepsilon}^0 dz+ \sum_{k=1}^{n} \int_{h_{k-1}}^h \mathbf{Q}'_k\boldsymbol{\kappa}zdz = \\ \Big[ \sum_{k=1}^{n} \mathbf{Q}'_k (h_k-h_{k-1}) \Big] \boldsymbol{\varepsilon}^0 + \Big[\frac{1}{2}\sum_{k=1}^{n} \mathbf{Q}'_k(h_k^2-h_{k-1}^2 \Big] \boldsymbol{\kappa} \Rightarrow \\ \mathbf{N} = \mathbf{A} \boldsymbol{\varepsilon}^0+\mathbf{B} \boldsymbol{\kappa} $$

Moment resultants:

$$ \mathbf{M} = \sum_{k=1}^{n} \int_{h_{k-1}}^h \boldsymbol{\sigma}'zdz = \sum_{k=1}^{n} \int_{h_{k-1}}^h \mathbf{Q}'_k\boldsymbol{\varepsilon}'zdz = \sum_{k=1}^{n} \int_{h_{k-1}}^h \mathbf{Q}'_k(\boldsymbol{\varepsilon}^0 + z \boldsymbol{\kappa})zdz = \sum_{k=1}^{n} \int_{h_{k-1}}^h \mathbf{Q}'_k\boldsymbol{\varepsilon}^0 z dz+ \sum_{k=1}^{n} \int_{h_{k-1}}^h \mathbf{Q}'_k\boldsymbol{\kappa}z^2 dz = \\ \Big[\frac{1}{2}\sum_{k=1}^{n} \mathbf{Q}'_k (h_k^2-h_{k-1}^2) \Big] \boldsymbol{\varepsilon}^0 + \Big[\frac{1}{3}\sum_{k=1}^{n} \mathbf{Q}'_k(h_k^3-h_{k-1}^3 )\Big] \boldsymbol{\kappa} \Rightarrow \\ \mathbf{M} = \mathbf{B} \boldsymbol{\varepsilon}^0+\mathbf{D} \boldsymbol{\kappa} $$

where

\begin{equation} \begin{aligned} &\mathbf{A} = \sum_{k=1}^{n} \mathbf{Q}'_k (h_k-h_{k-1}) \\ &\mathbf{B} = \frac{1}{2}\sum_{k=1}^{n} \mathbf{Q}'_k (h_k^2-h_{k-1}^2) \\ &\mathbf{D} = \frac{1}{3}\sum_{k=1}^{n} \mathbf{Q}'_k (h_k^3-h_{k-1}^3) \end{aligned} \tag{17} \end{equation}

Finally,

\begin{equation} \begin{bmatrix} \mathbf{N} \\ \mathbf{M} \end{bmatrix}= \begin{bmatrix} \mathbf{A} & \mathbf{B} \\ \mathbf{B} & \mathbf{D} \end{bmatrix} \begin{bmatrix} \boldsymbol{\varepsilon^0} \\ \boldsymbol{\kappa} \end{bmatrix} \tag{18} \end{equation}

Disclaimer:This site is about polymer composites, designed for educational purposes. Consumption and use of any sort & kind is solely at your own risk.
Fair use: I spent some time making all the pages, and even the figures and illustrations are my own creations. Obviously, you may steal whatever you find useful here, but please show decency and give some acknowledgment if or when copying. Thanks! Contact me: nils.p.vedvik@ntnu.no www.ntnu.edu/employees/nils.p.vedvik