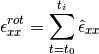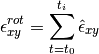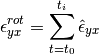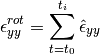Rotationless Strains¶

Note

The rotationless strains must be seen as experimental. The strains are acumulated, i.e. the strain values are a sum of all previous strain increments. In DIC there will always be a degree of noise in the measured displacement field. Thus, an acumulated strain value will also accumulate the noise components from all preceeding images.

Hint

It may be beneficial to carry out some degree of filtering of the raw DIC displacement field before trying to use the rotationless strain.

In a 2D-DIC analysis, a two-dimensional displacement field 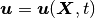$\bm{u}=\bm{u}(\bm{X},t)$ is measured. Here 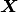$\bm{X}$ denotes a position in the reference coordinate system. $t$ denotes the time, usually associated to the image ID in a sequence of images.

For any position 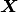$\bm{X}$ and any time $t$ the two-dimensional deformation gradient may be calculated as:

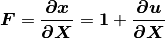
$\bm{F} = \frac{\bm{\partial x}}{\bm{\partial X}} = \bm{1} + \frac{\bm{\partial u}}{\bm{\partial X}}$

First, a polar decomposition is applied to the deformation gradient, splitting the deformation gradient in a rotation matrix 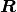$\bm{R}$ and a strecth matrix $\bm{U}$ :

$\bm{F} = \bm{RU}$

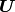The velocity gradient 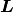$\bm{L}$ is defined as

$\bm{L} = \bm{\dot{F}} \bm{F}^{-1} = \frac{\bm{F}(\bm{X},t_i) - \bm{F}(\bm{X},t_{i-1})}{dt} \bm{F}_i^{-1}$

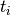where $\bm{\dot{F}}$ is the time derivative of the deformation gradient, $t_i$ indicates the current time step and $dt=t_i - t_{i-1}$ is the duration of the last timestep.

The rate of deformation tensor $\bm{D}$ is further defined as:

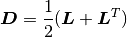
$\bm{D} = \frac{1}{2}(\bm{L} + \bm{L}^T)$

And then the rotationless deformation tensor $\hat{\bm{D}}$ is found as:

$\bm{\hat{D}} = \bm{R}^T \bm{D} \bm{R}$

The rotationless strain increments is given by the components of the rotationless deformation tensor:

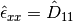
${\hat{\epsilon}}_{xx} = \hat{D}_{11}$

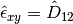
${\hat{\epsilon}}_{xy} = \hat{D}_{12}$

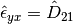
${\hat{\epsilon}}_{yx} = \hat{D}_{21}$

${\hat{\epsilon}}_{yy} = \hat{D}_{22}$

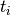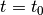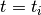The rotationless strain at a time $t_i$ is calculated as a sum of all strain increments from the start of the test $t=t_0$ until the current time $t=t_i$ :

${\epsilon}_{xx}^{rot} = \sum_{t = t_0}^{t_i}{{\hat{\epsilon}_{xx}}}$

${\epsilon}_{xy}^{rot} = \sum_{t = t_0}^{t_i}{{\hat{\epsilon}_{xy}}}$

${\epsilon}_{yx}^{rot} = \sum_{t = t_0}^{t_i}{{\hat{\epsilon}_{yx}}}$

${\epsilon}_{yy}^{rot} = \sum_{t = t_0}^{t_i}{{\hat{\epsilon}_{yy}}}$