Logarithmic Strains¶

In a 2D-DIC analysis, a two-dimensional displacement field 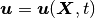$\bm{u}=\bm{u}(\bm{X},t)$ is measured. Here 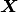$\bm{X}$ denotes a position in the reference coordinate system. $t$ denotes the time, usually associated to the image ID in a sequence of images.

For any position 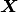$\bm{X}$ and any time $t$ the two-dimensional deformation gradient may be calculated as:

$\boldsymbol{F} = \frac{\bm{\partial x}}{\bm{\partial X}} = \bm{1} + \frac{\bm{\partial u}}{\bm{\partial X}}$

The two-dimensionalright Cauchy- Green deformation tensor 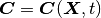$\bm{C}=\bm{C}(\bm{X},t)$ is then calculated as:

$\bm{C} = \bm{F^T}\bm{F}$

The in-plane principal streches 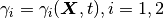${\gamma}_i = {\gamma}_i(\bm{X},t), i = 1,2$ are found by solving the eigenvalue problem for the right Cauchy-Green deformation tensor:

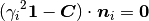
$({{\gamma}_i}^2 \bm{1} - \bm{C}) \cdot \bm{n}_i = \bm{0}$

where $\bm{n}_i$ , the eigenvectors, gives the principal directions of the right Cauchy-Green deformation tensor.

Note

Because of the two-dimensional nature of the DIC measurements, the third principal direction 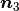$\bm{n}_3$ is assumed to be normal to the surface of the specimen, i.e. the shear strains through the thickness of the specimen are assumed negligible.

The in-plane principal logarithmic strains are then calculated from the principal stretches:

${\epsilon}_i = ln({\gamma}_i), i = 1,2$

where the rotation of the principal strains is given by the eigenvectors $\bm{n}_i$ .

Note

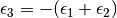In eCorr it is also possible to obtain the third principal strain component ${\epsilon}_3$ , i.e. through the thickness. However, this is only valid where we can assume negligible elastic strains and plastic incompressibility. Then, the third component is estimated as follows: ${\epsilon}_3 = -({\epsilon}_1 + {\epsilon}_2)$ .

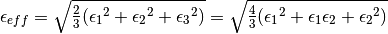
Further, an effective strain measure ${\epsilon}_{eff}$ based on the von Mises norm is available. This is defined as ${\epsilon}_{eff} = \sqrt{\frac{2}{3}({{\epsilon}_1}^2 + {{\epsilon}_2}^2 + {{\epsilon}_3}^2)} = \sqrt{\frac{4}{3}({{\epsilon}_1}^2 + {{\epsilon}_1}{{\epsilon}_2} + {{\epsilon}_2}^2)}$

A two-dimensional strain matrix is established using the calculated principal strains:

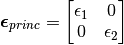
$\bm{\epsilon}_{princ} = \begin{bmatrix} {\epsilon}_1 & 0 \\ 0 & {\epsilon}_2 \end{bmatrix}$

Now, this principal strain matrix $\bm{\epsilon}_{princ}$ is associated with the principal directions $\bm{n}_i$ . To obtain the strain matrix for a specific direction, the matrix may be rotated using a two-dimensional rotation matrix $\bm{R}$ :

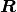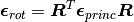
$\bm{\epsilon}_{rot} = \bm{R}^T \bm{\epsilon}_{princ} \bm{R}$

Thus, by using the rotation provided by the principal directions $\bm{n}_i$ , the strain matrix can be rotated back to the coordinate domain, giving the logarithmic coordinate strains:

$\bm{\epsilon}_{coord} = \begin{bmatrix} {\epsilon}_{xx} & {\epsilon}_{xy} \\ {\epsilon}_{yx} & {\epsilon}_{yy} \end{bmatrix} = \bm{R}^T \bm{\epsilon}_{princ} \bm{R}$

Note

When time-series of strains are plotted or exported in eCorr, the strains are always calculated in the center of an element.