The likelihood is computed on the basis of ![]() contrasts
contrasts
![]() between the observed
standardized gene frequencies. The covariance matrix of
these contrasts is returned by function covpred. Two
arguments are required; the name of the migration model FUN, the parameter vector theta.
between the observed
standardized gene frequencies. The covariance matrix of
these contrasts is returned by function covpred. Two
arguments are required; the name of the migration model FUN, the parameter vector theta.
Function covobs estimates the covariances from the observations directly using the estimator
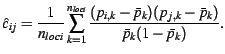 |
(4) |
The predicted and observed covariances can be compared through plotting them with the covplot function. Arguments are the computed predicted and observed covariance matrices. The following call
> covplot(covpred(steppingstone,fit1$par),covobs(p))produced the plot shown in Figure 2. Two additional optional arguments can be given; mfcol specifying the number of rows and columns in the plot, and file specifying the name of a postscript file (used as alternative output). The interpretation of these type of plots is discussed in Tufto et al. (1998).
Function covpred computes (an approximation) of the
covariances under a given model, conditioned on the observed
gene frequency means at each locus. The unconditional
covariances may also be of interest. These can be computed
by function courgeau, called with the migration matrix
M and the vector of effective population sizes Ne as arguments. This function rewrites the matrix
equation (Tufto et al., 1996, eq. 7) to a system of ![]() equations
(Tufto et al., 1996, eq. A.4 and A.5) and solves these. It may be noted that the
returned unconditional covariances (which are exact to the
extent that the order of the events in the life cycle can be
ignored) can differ greatly from the conditional ones,
especially if the long range rate of migration is low such
that the gene frequency vector is in one of the states
equations
(Tufto et al., 1996, eq. A.4 and A.5) and solves these. It may be noted that the
returned unconditional covariances (which are exact to the
extent that the order of the events in the life cycle can be
ignored) can differ greatly from the conditional ones,
especially if the long range rate of migration is low such
that the gene frequency vector is in one of the states
![]() or
or
![]() for long periods of time.
for long periods of time.