TMM4175 Polymer Composites

Home About Python Links Table of Contents

CASE STUDY: Transformation by substitution of axes¶

Problem statement: Strains, stresses and engineering constants are given in a coordinate system 1,2,3 illustrated in Figure-1. Transform strains, stresses and enginnering constants to the coordinate system x,y,z.

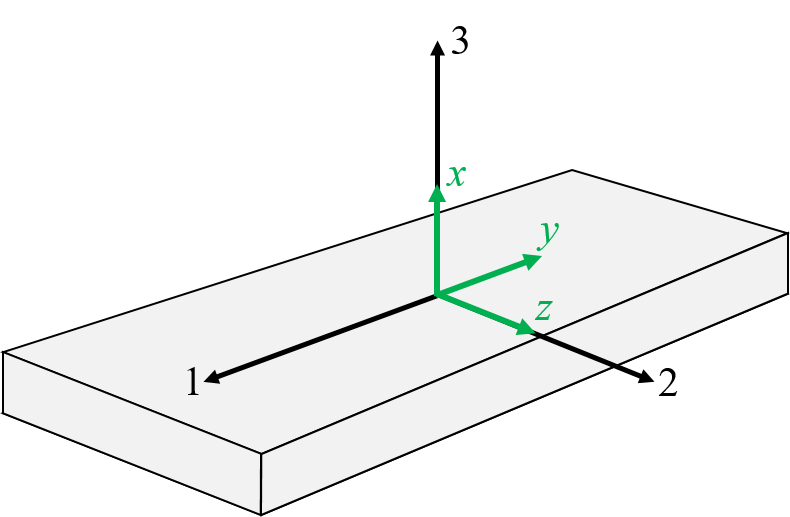
Figure-1

Strains¶

The transformation of normal strains are straight forward by simple substituion of axes and therefore, indices:

\begin{equation} \varepsilon_{x}=\varepsilon_{3}, \quad \varepsilon_{y}=\varepsilon_{1}, \quad \varepsilon_{z}=\varepsilon_{2} \end{equation}

For the shear strains we must pay slightly more attention. Figure-2 (b) shows a deformed body representing, by definition, a positive shear strain $\gamma_{13}$. The same body from the same perspective is illustrated in Figure-2 (a) with the axes y and x. Now, flipping the axes and the deformed body as illustrated in Figure-2 (c), and we can draw the conclusion:

\begin{equation} \gamma_{yx}=-\gamma_{13} \end{equation}

Figure-2

The same logic applies for the relation between $\gamma_{yz}$ and $\gamma_{12}$: \begin{equation} \gamma_{yz}=-\gamma_{12} \end{equation}

while the remaining shear strain is directly related:

\begin{equation} \gamma_{zx}=\gamma_{23} \end{equation}

Since $\gamma_{ji}=\gamma_{ij}$, the summary can be written as

\begin{equation} \begin{bmatrix} \varepsilon_{x} \\ \varepsilon_{x} \\ \varepsilon_{x} \\ \gamma_{yz} \\ \gamma_{xz} \\ \gamma_{xy} \end{bmatrix}= \begin{bmatrix} \varepsilon_{3} \\ \varepsilon_{1} \\ \varepsilon_{2} \\ -\gamma_{12} \\ \gamma_{23}\\ -\gamma_{13} \end{bmatrix} \end{equation}

Stresses¶

The arguments made for strains can easilly be adapted to stresses as well. Hence,

\begin{equation} \begin{bmatrix} \sigma_{x} \\ \sigma_{x} \\ \sigma_{x} \\ \tau_{yz} \\ \tau_{xz}\\ \tau_{xy} \end{bmatrix}= \begin{bmatrix} \sigma_{3} \\ \sigma_{1} \\ \sigma_{2} \\ -\tau_{12} \\ \tau_{23}\\ -\tau_{13} \end{bmatrix} \end{equation}

Engineering constants¶

\begin{equation} E_x=E_3 \\ E_y=E_1 \\ E_z=E_2 \\ G_{xy}=G_{31}=G_{13} \\ G_{xz}=G_{32}=G_{23} \\ G_{yz}=G_{12} \\ \nu_{xy}=\nu_{31}=\nu_{13} \frac{ E_3 }{E_1} \\ \nu_{xz}=\nu_{32}=\nu_{23} \frac{ E_3 }{E_2} \\ \nu_{yz}=\nu_{12} \end{equation}

Remember that

\begin{equation} G_{ji}=G_{ij} \end{equation}

while

\begin{equation} \frac{ \nu_{ji} }{E_j} = \frac{ \nu_{ij} }{E_i} \end{equation}

Left as exercise: Verify the specific transformation in this case study using the relations for general transformation.

Disclaimer:This site is about polymer composites, designed for educational purposes. Consumption and use of any sort & kind is solely at your own risk.
Fair use: I spent some time making all the pages, and even the figures and illustrations are my own creations. Obviously, you may steal whatever you find useful here, but please show decency and give some acknowledgment if or when copying. Thanks! Contact me: nils.p.vedvik@ntnu.no www.ntnu.edu/employees/nils.p.vedvik