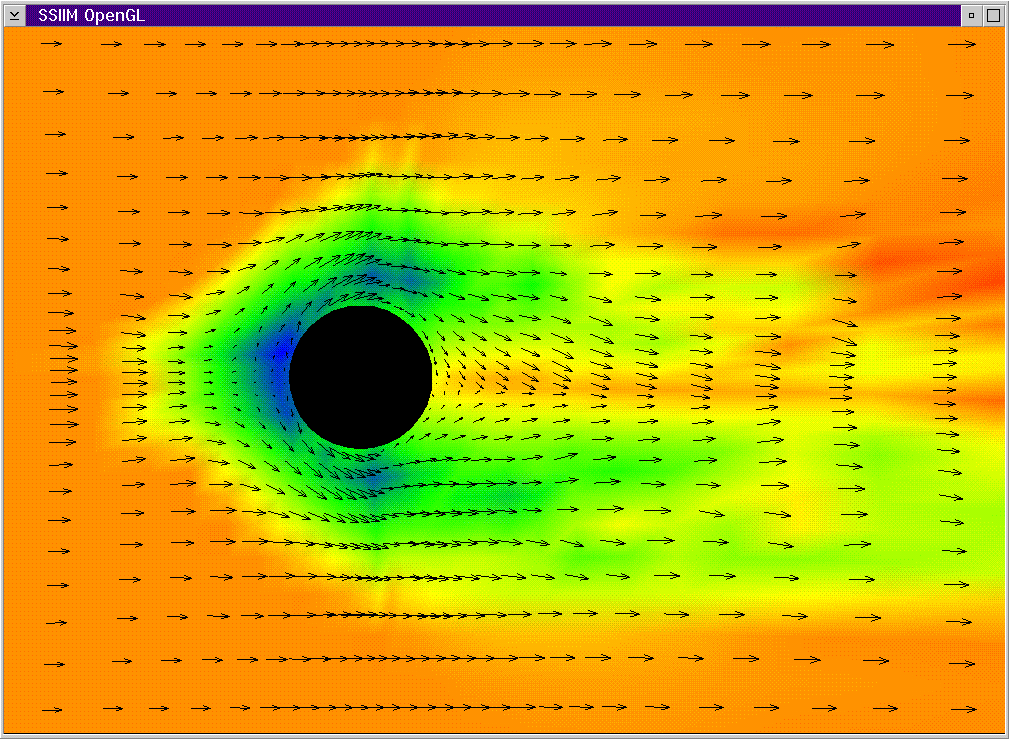
The geometry is seen from above. The velocity vectors are at a level close
to the bed. The colors show the bed elevation. Blue is minimum elevation, and
red is maximum elevation.
This case is a calculation of local scour depth. The numerial model is based on several modules which calculates water flow, sediment movements, water surface location and bed geometry changes. The water flow module solves the Reynolds-averaged Navier-Stokes equations with the k-epsilon turbulence model. Time-terms are included. The location of the water surface is calculated by extrapolating the pressure from the inner cells to the water surface. A reference level is given at a grid cell located at the downstream boundary, where the water surface is not allowed to move. The pressure in this cell is taken as a reference pressure, and a pressure defect at each surface cell is calculated by subtracting this reference pressure. The pressure defect is then used to move the water surface. Since the time-terms are included in the calculation, the water flow module calculates the velocities and the water surface with time. Also, the k-þ model is used for calculating the shear stress at the bed. This is used by the sediment calculation module.
The sediment transport is calculated with the convection-diffusion equation for the sediment concentration. A formula for concentration at the bed as a function of the shear stress is used as a boundary condition. The concentration is "forced" on the bed boundary finite volumes in a similar manner as the boundary condition for epsilon in the k-epsilon model. The convection-diffusion equation is not solved for the cells closest to the bed. Sediment continuity for these cells are therefore usually not satisfied. The discrepancy in continuity is used to calculate changes in the bed levels. This method also has the advantage of simulating the interaction between the sediment that move close to the bed and the sediment that move in suspension.
The water flow field is solved simultaneously with the sediment calculation. The models include time-dependency with transient terms, and calculation of the free surface is also done. An adaptive grid is used, which follows the changes in bed and water surface elevations. The model gives the development of the three-dimensional scour hole.
When bed movements occur, there are important phenomena that affect the sediment at the bed. When the bed slope approaches the angle of repose, the critical shear stress goes to zero. This causes instabilities. To avoid this, the angle between the grid lines at the bed and the horizontal plane was controlled. The bed configuration was not allowed to move in such a way that the bed slope became steeper than the angle of repose for the bed material. This procedure prevented both unrealistic results and instabilities.
For a sloping bed the critical shear stress will change. Two formulas are used for changing the critical shear stress as a function of the bed slope parallel and normal to the velocity vector. These formulas are essential for the correct calculation of the maximum scour depth and the shape of the scour hole.
The numerical model is tested on a case with a circular vertical cylinder placed in a flume. The flume is 7.5 meter wide and 22 meter long flume, with a vertical circular cylinder with diameter 1.5 meter. The upstream water velocity is 2 m/s. The scour depth in front of the cylinder is presented as time series. The maximum depth of the scour hole varies between 1.6-2.5 meters depending on the values of the input parameters. The results compare well with empirical formulas for maximum scour depth, as the results from the formulas varies in the same range as the results from the numerical model.
The geometry is seen from above. The velocity vectors are at a level close
to the bed. The colors show the bed elevation. Blue is minimum elevation, and
red is maximum elevation.
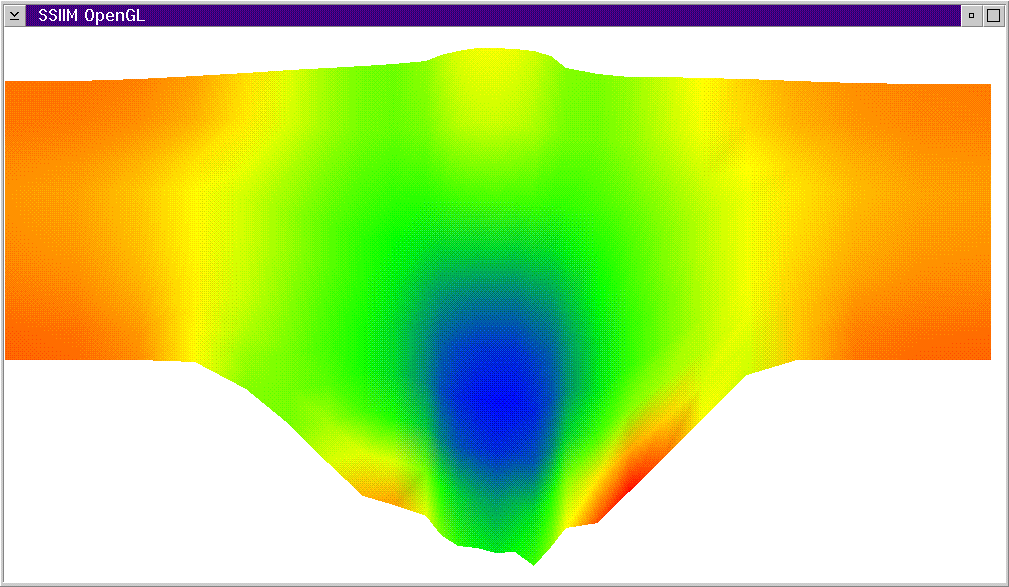Cross-section following the front of the cylinder, where the colors indicate
vertical velocity. Blue are velocities in the downward direction while red is
vertical velocity close to zero. Also note the shape of the scour hole and the
water surface elevation in front of the cylinder.
Longitudinal profile along the centerline of the geometry. The colors show
the pressure minus the hydrostatic component. Note that the pressure in
front of the cylinder is non-hydrostatic. (The colors change with depth)