

The model was buildt of concrete, and it was assumed the sediments would fill the reservoir within reasonably short time. Sand was therefore filled up to a horizontal level above the bottom of the flushing gates. The model was then carefully filled with water, to avoid disturbance of the sediments, with the flushing gates closed. When the water level was at a given distance above the sediments, the gates were opened. The water level then dropped, and erosion of the sand started. The downstream water level decreased rapidly initially, and slower towards the end of the flushing. The inflowing water discharge was kept constant. The flushing lasted for 2 1/2 hours, or 9000 seconds. Then cross-sections of the bed was measured.
The numerical model solved the Navier-Stokes equations and the convection-diffusion equation for sediment transport on an unstructured 3D grid with a mixture of hexahedral and tetrahedral cells. The grid was regenerated for each 10th time step, giving 90 regenerations for the calculation. For each regeneration, the old values were interpolated to the new grid. The number of grid cells changed over time, from about 6000 at the beginning to about 3000 at the end of the computation. The shape of the cells also changed in the horizontal plane, along the boundary. The grid regeneration and the interpolation took under 0.5 % of the computational time.
The k-epsilon model was used for turbulence, together with wall laws for rough boundaries. The roughness was calculated from the computed bed grain size distribution and the bedform height. Bedforms were calculated by van Rijn's method. Both suspended load and bed load were calculated by the formulas given by van Rijn. The decrease in effective shear stress as a function of grain/bedform roughness was taken into account. The critical shear stress for the particles was calculated by Shield's curve, and corrected for bed slope and the water flow direction.

Photograph of physical model study. The dimensions are about 10 meters from the confluence (right) to the dam (lower left). The entrance is at the top of the picture.

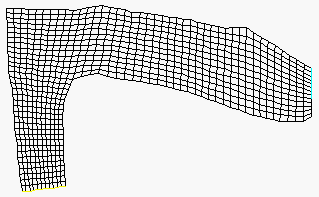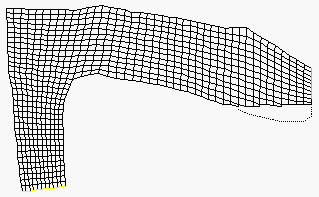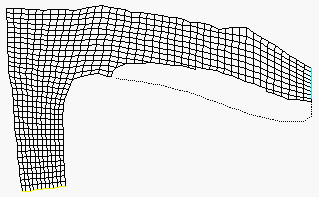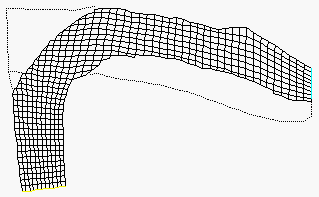
The right figure shows the grid, and how it changes over time. There are 9000 seconds in the calculation, and there is an image for each 1000 second. The left figure shows the bed elevation, where the blue lines are the deepest part of the bed, and red is the highest bed elevations. The water flow direction is from the lower left corner to the right.

The two first images in the series show longitudinal profiles of the grid. The following images show cross-sections of the downstream part of the geometry. Note the hexahedral cells close to the bed. The figures are strongly distorted in the vertical direction.


The left picture show the bed evolution over time, with 1000 seconds between each picture. The colors are vertical bed levels. The right picture shows a rotating view of the bed at the end of the flushing. The figures are strongly distorted in the vertical direction.
|
|
|