
This study looks at numerical modeling of turbulent flow around a circular cylinder placed vertically in a flume. This case has previously been calculated with a steady state three-dimensional numerical model (Olsen and Melaaen, 1993). However, the flow field is unsteady at cylinder Reynolds numbers below 106, so the numerical model did not simulate the transient eddies behind the cylinder. A number of studies of transient two-dimensional numerical modeling of turbulent flow behind a body have been done. The conclusion is that a body with sharp edges where the flow separates can be simulated with standard turbulence models and a relatively coarse grid. For a circular cylinder there are no sharp separation points. Transient simulations have then been successful only with a modified turbulence model. Therefore, some part of the numerical model have to be modified.
The numerical model is based on the Reynolds averaged Navier-Stokes equations. The k-epsilon model is used to resolve the Reynolds stress terms. The control volume method is used for discretization together with the Power Law Scheme, which is a first-order upstream method. An implicit method is used for time integration. The SIMPLE method is used for the pressure coupling. Zero gradient boundary conditions are used for all variables at the outflow boundary and at the water surface except for the turbulent kinetic energy, k, which is set to zero at the water surface. Wall laws for rough boundaries are used at the side walls, the bed and at the cylinder wall
Water flow is simulated around a cylinder placed vertically in a flume. The grid has 20 cells in the vertical direction with equal vertical size. The diameter of the cylinder is 0.4 m, and the flume is 0.4 m deep, 1.4 m wide and 2.1 m long. The inflow velocity is 0.375 m/s. The cylinder Reynolds number is 150 000. The time step is 0.05 seconds, with 40 inner iterations pr. time step.
Initial simulations were done with smooth wall laws and rough wall laws with low roughness. This gave a steady state solution. Since vortex shedding occurs, these results were not satisfactory. Instead an algorithm was used where the roughness was varied according to the velocity of the flow close to the cylinder boundary. If the velocity was equal to the velocity upstream of the cylinder, a roughness of 5 cm was used. If the velocity was zero, a roughness of 0.001 mm was used. A linear variation was used between these points. This produced the transient vortexes behind the cylinder.
Beside changing the roughness of the wall, also other parameters were varied without visible effect. These variables were the magnitude of the time step, number of inner iterations pr. time step, boundary conditions, relaxation factors and grid size close to the wall. Also, to start the oscillations, the horizontal velocity profile at the upstream boundary was skewed for the first seconds of the calculations. After 6 seconds, the velocity profile became symmetric instantaneously. However, for the final calculation, symmetric upstream boundary conditions were used from the start, and the oscillations still evolved with time.
The time series gives a frequency of 0.21. This gives a Strouhal number of 0.22 or 0.16 depending on whether the increased velocity because of decrease of the cross-sectional area of the flume is taken into account.

Map of velocities midway between water surface and bed. Colors show the magnitude of the horizontal velocity.

Map of velocities midway between water surface and bed. Colors show the vertical velocity.
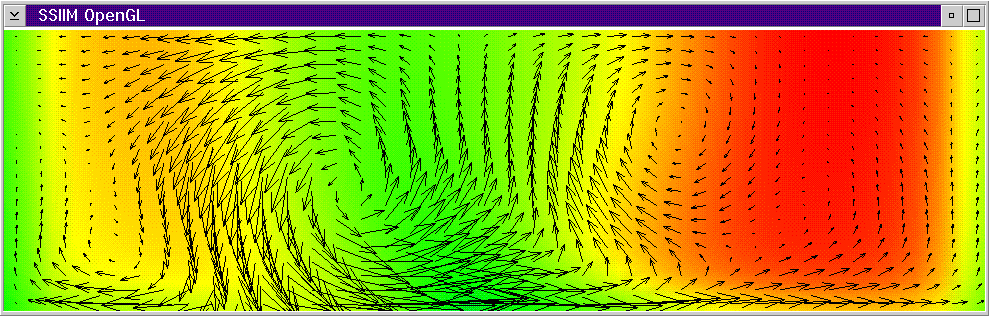
Map of velocities at end cross-section. Colors show the magnitude of the velocity in the direction towards the viewplane.
|
|