7.1 Poiseuille flow in a compliant vessel
Simplified solution for flow in compliant vessel. In general Navier-Stokes equations for blood, Navier equations for vessel wall, must be solved simultaneously. Simplification; Poiseuille flow for the fluid, \( p(A) \) relation for vessel wall.
Poiseuille flow relates pressure gradient to volume flow: $$ \begin{equation} \frac{dp}{dx} = - \frac{8 \mu}{\pi a^{4}} \; Q = - \frac{8\pi\mu}{A^2} \; Q \tag{7.1} \end{equation} $$
Compliance \( \D C = \partd{A}{p} \) $$ \begin{equation} \frac{dp}{dx} = \partd{p}{A} \, \frac{dA}{dx} = \frac{1}{C} \; \frac{dA}{dx}= -\frac{8\pi\mu}{A^2} \; Q \tag{7.2} \end{equation} $$ $$ \begin{equation} A^2\; \frac{dA}{dx} = \frac{1}{3} \; \frac{d}{dx} \left ( A^3 \right ) = - 8 \pi \mu C Q \tag{7.3} \end{equation} $$
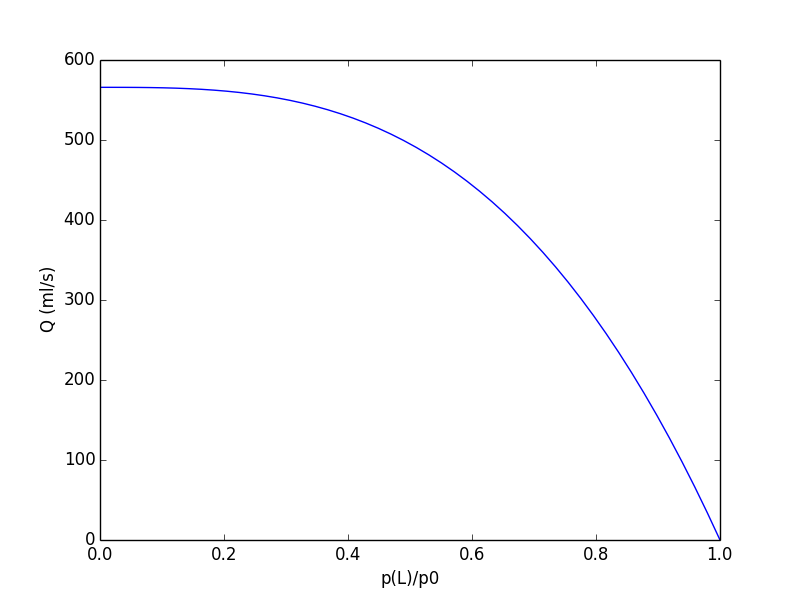
Figure 67: Flow versus normalized outlet pressure for Poiseuille flow in compliant pipe.
Integration $$ \begin{equation} A(x)^3 = A(0)^3 - 24 \pi \mu C Q x \tag{7.4} \end{equation} $$
Constitutive model: \( A(p) = A_0 + C \; (p-p_0) \)
Pressure and flow for stationary flow in compliant vessel $$ \begin{equation} Q(x) = \frac{A(0)^3-A(x)^3}{24\pi\mu C x}, \quad p(x) = p_0 + \frac{A(x) - A(0)}{C} \tag{7.5} \end{equation} $$